УДК 517.57: 519.6
МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПОЛЕЙ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ В МНОГОУГОЛЬНЫХ ОБЛАСТЯХ
Астионенко И.А., Гучек П.И., Литвиненко Е.И., Хомченко А.Н.
Постановка проблемы
Полигональные дискретные элементы представляют интерес для расчета электростатических и стационарных температурных полей. Как правило, полигональная область разбивается на треугольные области, что приводит к увеличению объема вычислений [1]. В данной работе рассматривается дискретный элемент в форме правильного пятиугольника (пентагон). На пентагоне авторами построен унитарный базис лагранжевой интерполяции и исследуются свойства этого базиса.
Анализ последних исследований и публикаций
Как известно, существует два подхода к определению гармоничности функции: дифференциальный и интегральный. Дифференциальный критерий формулируется следующим образом: функция ![]() , имеющая непрерывные частные производные второго порядка в области
, имеющая непрерывные частные производные второго порядка в области ![]() и удовлетворяющая внутри
и удовлетворяющая внутри ![]() уравнению Лапласа:
уравнению Лапласа:
|
|
(1) |
называется гармонической функцией в области ![]() [2].
[2].
Интегральные критерии были получены при решении задачи Дирихле для уравнения Лапласа в круге [3]:
дан круг радиуса ![]() с центром в начале координат и на его окружности задана некоторая функция
с центром в начале координат и на его окружности задана некоторая функция![]() , где
, где ![]() - полярный угол. Требуется найти функцию
- полярный угол. Требуется найти функцию ![]() , непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа
, непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа
|
|
(2) |
и на граничной окружности принимающую заданные значения:
|
|
(3) |
Решение уравнения Лапласа для круговой области в виде интеграла по границе круга (интеграла Пуассона)
|
|
(4) |
было получено С. Пуассоном в начале XIX века [3].
В 1906 году Кёбе сформулировал и доказал обратную теорему:
если функция ![]() непрерывна в области
непрерывна в области ![]() и принимает в каждой точке
и принимает в каждой точке ![]() из
из ![]() значение, равное среднему арифметическому значений на любой окружности
значение, равное среднему арифметическому значений на любой окружности ![]() с центром в точке
с центром в точке ![]() , целиком лежащей в
, целиком лежащей в ![]() , то функция
, то функция ![]() гармонична в
гармонична в ![]() :
:
|
|
(5) |
где ![]() - окружность радиуса
- окружность радиуса ![]() с центром в точке
с центром в точке ![]() ,
,
![]() - функция, заданная на границе круга,
- функция, заданная на границе круга, ![]() - элемент дуги окружности.
- элемент дуги окружности.
Заметим, что если в формуле (4) взять ![]() , то ядро Пуассона обращается в единицу, и получается значение функции в центре круга в виде среднего значений функции
, то ядро Пуассона обращается в единицу, и получается значение функции в центре круга в виде среднего значений функции ![]() на границе (формула 3). Если формула Кёбе позволяет вычислять среднее значение функции в центре, то формула Пуассона дает возможность восстанавливать гармоническую функцию во всех точках круга. Однако, для точек, которые расположены ближе к границе области, возникают большие погрешности за счет увеличения влияния ядра Пуассона, нарушается свойство среднего и не выполняется теорема максимума для гармонической функции [2;3].
на границе (формула 3). Если формула Кёбе позволяет вычислять среднее значение функции в центре, то формула Пуассона дает возможность восстанавливать гармоническую функцию во всех точках круга. Однако, для точек, которые расположены ближе к границе области, возникают большие погрешности за счет увеличения влияния ядра Пуассона, нарушается свойство среднего и не выполняется теорема максимума для гармонической функции [2;3].
Эти результаты в 1925 г. были обобщены И.И. Приваловым на двумерный случай (двойной интеграл для круга) и на трехмерный случай (поверхностный интеграл по сфере и интеграл по объему шара) [4]. Теорема И.И. Привалова для функции двух аргументов формулируется следующим образом [4]:
непрерывная функция ![]() в области G является гармонической тогда и только тогда, когда во всякой точке
в области G является гармонической тогда и только тогда, когда во всякой точке ![]() , начиная с достаточно малого радиуса
, начиная с достаточно малого радиуса ![]() , выполняется свойство среднего, т.е.
, выполняется свойство среднего, т.е.
|
|
(6) |
где ![]() -функция, заданная в круге радиуса
-функция, заданная в круге радиуса ![]() ,
,
![]() - круговая область радиуса
- круговая область радиуса ![]() с центром в точке
с центром в точке ![]() ,
,
![]() - элемент площади.
- элемент площади.
Таким образом, И.И. Приваловым был предложен интегральный критерий гармоничности, а также установлена эквивалентность интегрального и дифференциального критериев. Интегральное условие (6) имеет важное значение для классической теории потенциала, так как функция ![]() , удовлетворяющая условию (6), является решением уравнения Лапласа (1) в области G.
, удовлетворяющая условию (6), является решением уравнения Лапласа (1) в области G.
В работе [5] установлено вероятностное содержание формул Кёбе и Привалова, рассмотрен дискретный аналог интегрального критерия гармоничности и дано вероятностное определение гармонической функции в круге. Авторами в статье [5] отмечено, что в формуле (5) отношение ![]() представляет собой плотность равномерного распределения (аналогично, в формуле (6) отношение
представляет собой плотность равномерного распределения (аналогично, в формуле (6) отношение ![]() ). Таким образом, формулы (5) и (6) представляют собой математическое ожидание функций, заданных соответственно на окружности и в круге. В терминах случайных блужданий
). Таким образом, формулы (5) и (6) представляют собой математическое ожидание функций, заданных соответственно на окружности и в круге. В терминах случайных блужданий ![]() - это вероятность перехода частицы из центра круга в элемент
- это вероятность перехода частицы из центра круга в элемент ![]() на границе. В формуле (6) отношение
на границе. В формуле (6) отношение ![]() - это вероятность случайного попадания точки в элемент площади
- это вероятность случайного попадания точки в элемент площади ![]() . При дискретизации интегралы (5) и (6) аппроксимируются интегральной суммой, а математическое ожидание – выборочным средним (в симметричных схемах случайных блужданий это среднее арифметическое) [5;6]. Переход к интегральным суммам открывает возможности для применения метода статистического моделирования (типа Монте-Карло), позволяет применять одношаговую схему случайных блужданий с несколькими прямолинейными маршрутами, выходящими на границу элемента. Таким образом, был получен дискретный аналог условия гармоничности функции для центра круга при равномерном распределении узлов на границе:
. При дискретизации интегралы (5) и (6) аппроксимируются интегральной суммой, а математическое ожидание – выборочным средним (в симметричных схемах случайных блужданий это среднее арифметическое) [5;6]. Переход к интегральным суммам открывает возможности для применения метода статистического моделирования (типа Монте-Карло), позволяет применять одношаговую схему случайных блужданий с несколькими прямолинейными маршрутами, выходящими на границу элемента. Таким образом, был получен дискретный аналог условия гармоничности функции для центра круга при равномерном распределении узлов на границе:
|
|
(7) |
где ![]() - число расчетных узлов на границе.
- число расчетных узлов на границе.
Далее формула (7) была обобщена на другие области с произвольным выбором точки старта. В схеме случайных блужданий наибольший интерес представляют полигональные области. Переходными вероятностями служат: в треугольнике – барицентрические координаты симплекса [5], в квадрате – базисные функции билинейной интерполяции [7], в правильном шестиугольнике – гексагональные базисные функции [8]. Условие гармоничности можно записать в виде:
|
|
(8) |
где ![]() - известные значения в вершинах полигонального дискретного элемента,
- известные значения в вершинах полигонального дискретного элемента,
![]() - базисные функции дискретного элемента.
- базисные функции дискретного элемента.
Базисные функции ![]() (весовые коэффициенты) удовлетворяют условию сохранения весового баланса в любой точке области и на ее границе:
(весовые коэффициенты) удовлетворяют условию сохранения весового баланса в любой точке области и на ее границе:
|
|
(9) |
Нерешенные ранее части общей проблемы и цели статьи
Представляет интерес построение базиса интерполяционного полинома (типа Лагранжа) для функции двух аргументов на пентагоне и проверка выполнения дифференциального и интегральных критериев гармоничности Кёбе и Привалова, вероятностная формулировка критерия гармоничности в дискретном элементе в форме правильного пятиугольника.
Основная часть
В работе рассмотрен дискретный элемент в форме правильного пятиугольника, вписанный в окружность единичного радиуса (рис.1). На данном элементе построено три системы базисных функций. Первый базис (5ПБ_1) построен с помощью алгебраического подхода на основании интерполяционной гипотезы Лагранжа:
|
|
(10) |
где ![]() - символ Кронекера [9].
- символ Кронекера [9].
Для построения базисной функции ![]() составлялась и решалась система линейных алгебраических уравнений. Авторам удалось построить базисные функции в виде полиномов.
составлялась и решалась система линейных алгебраических уравнений. Авторам удалось построить базисные функции в виде полиномов.
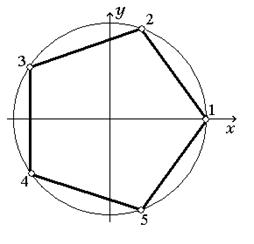
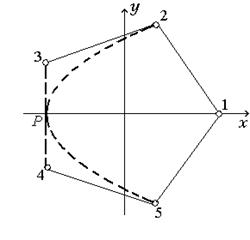
Рис. 1 Дискретный элемент Рис. 2 Композиция линий при
в форме правильного пятиугольника построении базисной функции ![]() в 5ПБ_2
в 5ПБ_2
Например, функция, ассоциируемая с узлом 1 в 5ПБ_1 (рис.1) имеет вид:
|
|
(11) |
Второй базис (5ПБ_2) построен с помощью геометрического подхода. Для построения базисной функции ![]() использована композиция прямой (3-4) и параболы, проходящей через 2-P-5 (рис. 2), где Р(-0,809 ;0):
использована композиция прямой (3-4) и параболы, проходящей через 2-P-5 (рис. 2), где Р(-0,809 ;0):
|
|
(12) |
При построении дробно-рационального базиса (5ДРБ) применялся подход, использованный в [1] при построении базиса гексагона. Базисная функция ![]() записывается в виде:
записывается в виде:
|
|
(13) |
Остальные функции во всех трех базисах были получены поворотом на угол ![]() .
.
Предложенные системы функций формы на правильном пятиугольнике были подвергнуты тестированию на гармоничность.
Дифференциальный критерий гармоничности по Лапласу сводится к проверке равенства:
|
|
(14) |
Каждая базисная функция 5ПБ_1 удовлетворяет дифференциальному критерию гармоничности. Функции 5ПБ_2 и 5ДРБ не являются гармоническими в смысле критерия Лапласа. Для 5ПБ_2 получены следующие невязки:
|
|
(15) |
|
|
|
|
|
(16) |
|
|
|
|
|
(17) |
|
|
|
|
|
(18) |
|
|
|
|
|
(19) |
Сумма невязок (15-19) обращается в ноль, что свидетельствует об их взаимной нейтрализации при ансамблировании пяти функций одного базиса. Аналогичная ситуация возникает в дробно-рациональном базисе на пентагоне.
Критерий Кёбе для дискретного элемента в форме правильного ![]() -угольника имеет вид:
-угольника имеет вид:
|
|
(20) |
где ![]() - периметр дискретного элемента,
- периметр дискретного элемента,
![]() - значение базисной функции в барицентре элемента.
- значение базисной функции в барицентре элемента.
Интегральный критерий Привалова записывается в виде:
|
|
(21) |
где ![]() - площадь дискретного элемента,
- площадь дискретного элемента,
![]() - значение базисной функции в барицентре элемента.
- значение базисной функции в барицентре элемента.
Проведенные вычисления по формулам (20) и (21) свидетельствуют, что базисные функции всех трех базисов на пентагоне удовлетворяют интегральным критериям гармоничности Кёбе и Привалова (табл. 1):
Табл. 1
|
|
5ПБ_1 |
5ПБ_2 |
5ДРБ |
|
Критерий Кёбе |
0,2 |
0,2 |
0,2 |
|
Критерий Привалова |
0,2 |
0,2 |
0,2 |
Обратим внимание на вероятностный смысл базисных функций дискретного элемента в форме пятиугольника. Сформулируем правила случайных блужданий в пятиугольнике:
пусть частица стартует из произвольной точки ![]() и с вероятностью
и с вероятностью ![]() переходит в узел
переходит в узел ![]() , при этом
, при этом
|
|
(22) |
В данной схеме ускоренных блужданий базисные функции ![]() играют роль переходных вероятностей.
играют роль переходных вероятностей.
Для проверки гипотезы о возможности замены апостериорных переходных вероятностей априорными была выполнена серия компьютерных экспериментов с блужданиями частицы в пентагоне. С одной стороны, переходная вероятность вычислялась как значение базисной функции в точке старта (априорная вероятность) (рис. 3). С другой стороны, переходная вероятность вычислялась как относительная частота поглощения частиц в узле ![]() . Во втором случае пентагон покрывался ортогональной сеткой для маршрутизации многошаговых зигзагообразных случайных блужданий (рис.4). Длина одной серии - 100000 частиц, количество серий - 10.
. Во втором случае пентагон покрывался ортогональной сеткой для маршрутизации многошаговых зигзагообразных случайных блужданий (рис.4). Длина одной серии - 100000 частиц, количество серий - 10.
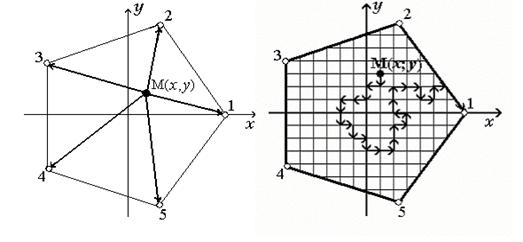
Рис. 3 Одношаговая 5-ти маршрутная Рис. 4 Маршрутизация случайных
схема случайных блужданий блужданий по узлам сетки
Расчеты подтверждают гипотезу о возможности замены апостериорных переходных вероятностей априорными (табл. 2). Наилучшее совпадение теоретических переходных вероятностей с экспериментальными получено для 5ДРБ и 5ПБ_1. Максимальное значение относительной погрешности для 5ПБ_1 составляет 0,67%, для 5ДРБ - 0,72%.
Табл. 2
Расчет переходных вероятностей в пентагоне
|
№ узла |
Расчетная точка |
Априорные вероятности |
Апостериорные вероятности |
||
|
5ПБ_1
|
5ПБ_2 |
5ДРБ |
|||
|
1 |
M2 (0,154; 0,475)
|
0,18109 |
0,20158 |
0,20016 |
0,18896 |
|
2 |
0,49999 |
0,52361 |
0,47639 |
0,49083 |
|
|
3 |
0,18071 |
0,20121 |
0,19984 |
0,19404 |
|
|
4 |
0,06914 |
0,03679 |
0,06178 |
0,06341 |
|
|
5 |
0,06905 |
0,03682 |
0,06182 |
0,06276 |
|
Анализ полученных результатов позволяет сформулировать вероятностный критерий гармоничности базисной функции на пентагоне:
функция называется гармонической на дискретном элементе, если математическое ожидание этой функции по элементу или его границе совпадает со значением функции в барицентре элемента.
Выводы и перспективы дальнейших исследований
Для правильного пятиугольника построены полиномиальные и дробно-рациональная системы базисных функций, позволяющие восстанавливать гармонические функции на пентагоне. Впервые сформулирован и обоснован вероятностный критерий гармоничности базисной функции на пентагоне.
Полученные результаты можно обобщить на задачи конструирования базисных функций призматических элементов с пятиугольным сечением и на другие правильные ![]() -угольники.
-угольники.
The existing of alternative bases is shown on the discrete element in the form of rectilinear pentagon: two systems of polynomial functions are built with the help of algebraic and geometric methods and fractionally-rational base is built as well. The examination of base functions as to harmonicity according to differential criterion and integral criteria is held, probable formulation of criterion of harmonicity on pentagon is given. The results of the research are of interest in the sums of boundary potentials theory.
1. Ishiguro M. Construction of Hexagonal Basis Functions Applied in the Galerkin-Type Finite Element Method: “J.Inf. Process”, 1984, v.7, № 2, p. 88-95.
2. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – М.: Наука, 1967.- 368 с.
3. Фарлоу С. Уравнения с частными производными для научных работников и инженеров. – М.: Мир, 1985. – 384 с.
4. Привалов И.И. Математический сборник. Т.32, 1925. С. 464-471.
5. Хомченко А.Н., Валько Н.В. Дискретные аналоги интегрального условия гармоничности функции. //Вестник Херсон.гос.техн.ун-та.- № 19. – Херсон: ХГТУ.-2004. – С. 17-19.
6. Хомченко А.Н., Валько Н.В. Гармонические функции и геометрическая вероятность //Вестник Херсон.нац.техн.ун-та.- № 22. – Херсон: ХГТУ.-2005. – С. 335-339.
7. Гучек П.И., Литвиненко Е.И., Буба М.С., Хомченко А.Н. Моделирование конечных элементов сирендипова семейства для исследования температурных полей //Проблеми пожежної безпеки. - К.: МВС України. – 1995. – С. 75-77.
8. Гучек П.И., Литвиненко Е.И., Хомченко А.Н. Геометрическое моделирование полиномиальных базисов шестиугольного элемента //Сб. тр. ІІІ Межд. конф. “Совр. пробл. геом. моделир.” - Мелитополь: ТГАТА, 1996. - С. 43.
9. Стренг Г., Фикс Дж. Теория метода конечных элементов.- М.: Мир.- 1977.- 349 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
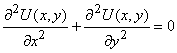 ,
,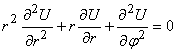
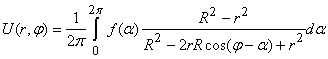
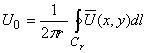 ,
, 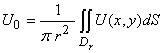 ,
, 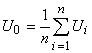 ,
, 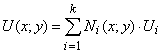 ,
, 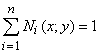 .
. 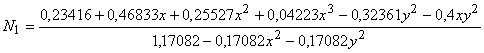 .
.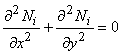
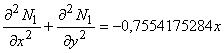 ,
,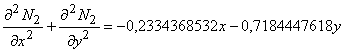 ,
,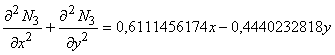 ,
,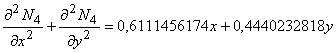 ,
,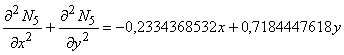 .
.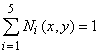 .
.