УДК 621.317
АвтоматизОВАНА сИСТЕМА вимірювань
фазових характеристик періодичних сигналів
на базі технології LabVIEW
Бабак В.П., Дегтярьов В.В, Куц Ю.В, Щербак Л.М.
Вступ. Фазові методи перетворення, обробки та
передачі інформації широко застосовуються в наукових дослідженнях і технічних
вимірюваннях. Ці методи дозволило вирішити ряд важливих науково-технічних
задач, пов’язаних з прецизійним вимірюванням кутів, відстаней, часових
інтервалів в радіотехніці, радіонавігації, радіоелектронній геодезії [1-6].
Значна область використання та ефективність фазових методів обумовили швидкі
темпи розвитку фазовимірювальної техніки у 80-90 роках двадцятого століття.
Були створені і серійно випускались фазометри серед яких Ф5126, Ф5131 (Україна),
Ф2-34, ФК2-35 (Росія) та ін., а також експериментальні зразки фазометрів з
підвищеними метрологічними характеристиками (точністю, динамічним діапазоном
сигналів, розширеним за межі інтервалу ![]() рад
діапазоном вимірювання, тощо) [7]. Нові можливості у підвищенні метрологічних
показників фазовимірювальної апаратури відкрито завдяки використанню цифрової
техніки і цифрових методів обробки сигналів, але на сьогодні не всі переваги цифрових
методів повністю реалізовані. Так, замість визначення фазових характеристик сигналів
через цифрову обробку інформаційних сигналів, виконувались додаткові проміжні
перетворення фазового зсуву в інші аналогові величини, наприклад, часовий
інтервал або значення напруг. При цьому сам вимірювальний сигнал часто
спотворювався, піддавався нелінійним перетворенням (обмеженню, диференціюванню
з метою визначення нуль-переходів та інші), що неминуче вело до зменшення
достовірної інформації про фазові характеристики сигналів. Таке “спрощення” для
можливості апаратурної реалізації стало джерелом виникненняя додаткових
методичних похибок, причиною виникнення ланцюга додаткових проблем – низької
завадостійкості, наявності “мертвих зон”, збільшення часу вимірювання тощо, і
обмежило можливості подальшого удосконалення фазовимірювальної апаратури.
Реалізація оптимальних алгоритмів оцінки фазових зсувів сигналів, які передбачають
застосування до сигналів таких операцій як множення, інтегрування, при реалізації
в аналоговій формі супроводжувалась значними апаратурними похибками [3,7].
рад
діапазоном вимірювання, тощо) [7]. Нові можливості у підвищенні метрологічних
показників фазовимірювальної апаратури відкрито завдяки використанню цифрової
техніки і цифрових методів обробки сигналів, але на сьогодні не всі переваги цифрових
методів повністю реалізовані. Так, замість визначення фазових характеристик сигналів
через цифрову обробку інформаційних сигналів, виконувались додаткові проміжні
перетворення фазового зсуву в інші аналогові величини, наприклад, часовий
інтервал або значення напруг. При цьому сам вимірювальний сигнал часто
спотворювався, піддавався нелінійним перетворенням (обмеженню, диференціюванню
з метою визначення нуль-переходів та інші), що неминуче вело до зменшення
достовірної інформації про фазові характеристики сигналів. Таке “спрощення” для
можливості апаратурної реалізації стало джерелом виникненняя додаткових
методичних похибок, причиною виникнення ланцюга додаткових проблем – низької
завадостійкості, наявності “мертвих зон”, збільшення часу вимірювання тощо, і
обмежило можливості подальшого удосконалення фазовимірювальної апаратури.
Реалізація оптимальних алгоритмів оцінки фазових зсувів сигналів, які передбачають
застосування до сигналів таких операцій як множення, інтегрування, при реалізації
в аналоговій формі супроводжувалась значними апаратурними похибками [3,7].
Розвиток засобів обчислювальної техніки, їх продуктивності та швидкодії, розвиток інформаційних технологій дозволяє на сьогодні впроваджувати більш складні алгоритми обробки інформації при побудові вимірювальних приладів і інформаційно-вимірювальних систем (ІВС). Стало доступним і економічно виправданим застосування методів спектрального аналізу на основі дискретного перетворення Фур’є, кореляційного аналізу, статистичного аналізу і обробки результатів вимірювань, чисельних методів тощо. Поява сучасного прикладного програмного забезпечення (пакети LabVIEW, MATLAB), орієнтованого на вирішення питань обробки сигналів та реалізацію основних функцій ІВС програмними засобами значно полегшує та скорочує час розробки нових вимірювальних приладів та ІВС, дозволяє дослідити різні варіанти ІВС з метою покращення їх метрологічних та експлуатаційних показників.
В статті аналізуються можливості застосування нових інформаційних технологій у вимірювальній техніці на прикладі створення фазовимірювальної системи на основі технології LabVIEW.
Постановка задачі. Необхідно розробити
структуру фазовимірювальної системи для вимірювання різниці фазових зсувів ![]() між гармонічними сигналами виду
між гармонічними сигналами виду
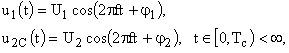 (1)
(1)
де ![]() - амплітуди сигналів,
- амплітуди сигналів, ![]() - частота (період
- частота (період ![]() ),
), ![]() ,
, ![]() -
межі частотного діапазону,
-
межі частотного діапазону, ![]() -
поточний час спостереження,
-
поточний час спостереження, ![]() - початкові
фазові зсуви,
- початкові
фазові зсуви, ![]() ,
, ![]() - інтервал часу спостереження
сигналів.
- інтервал часу спостереження
сигналів.
Для
сигналів ![]() (1) і
(1) і ![]() на
інтервалах часу
на
інтервалах часу ![]() виконується умова
ортогональності, тобто
виконується умова
ортогональності, тобто
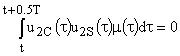 (2)
(2)
при значенні
вагової функції ![]() .
.
Використаємо дискретну ортогональну обробку сигналів як основний метод вимірювання фазових зсувів сигналів (1) на базі цифрової обробки.
Програмна частина системи реалізується в програмному пакеті LabVIEW.
Система
на ![]() основі зміни алгоритмів
і програмного забезпечення, статистичної обробки і візуалізації результатів
вимірювань повинна мати широке коло варіантів її реалізації.
основі зміни алгоритмів
і програмного забезпечення, статистичної обробки і візуалізації результатів
вимірювань повинна мати широке коло варіантів її реалізації.
Розв’язок. Повний розв’язок поставленої задачі розіб’ємо на декілька етапів.
1. Аналіз похибки вимірювання фазових
характеристик внаслідок неточного визначення інтервалу ортогональності.
Ортогональний метод [3,7] передбачає розклад одного з
сигналів (1), наприклад першого, в системі ортогональних функцій ![]() на інтервалі ортогональності
на інтервалі ортогональності ![]() . Для сигналів (1) результати розкладу
представляються у вигляді
. Для сигналів (1) результати розкладу
представляються у вигляді
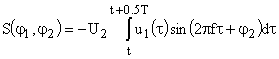 ,
, 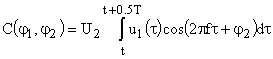 . (3)
. (3)
Визначивши
ці складові можна отримати модуль різниці фазових зсувів ![]() за формулою
за формулою
![]() , (4)
, (4)
де ![]() - знакова функція,
- знакова функція, ![]() - оператор
перетворення сигналів (3).
- оператор
перетворення сигналів (3).
Визначення
фазових зсувів за формулами (3), (4) в смузі частот ![]() викликає
певні складності, оскільки обчислення інтегралів в (3) має виконуватись на
інтервалах ортогональності, тобто на часових інтервалах кратних періоду сигналу,
який є апріорно не завжди є відомим. В той же час в більшості робіт, де
розглядається такий метод вимірювання, апріорно приймається, що період сигналу
відомий [3,7]. Для часу інтегрування
викликає
певні складності, оскільки обчислення інтегралів в (3) має виконуватись на
інтервалах ортогональності, тобто на часових інтервалах кратних періоду сигналу,
який є апріорно не завжди є відомим. В той же час в більшості робіт, де
розглядається такий метод вимірювання, апріорно приймається, що період сигналу
відомий [3,7]. Для часу інтегрування ![]() умова
ортогональності (2) порушується і виникає систематична похибка вимірювання фазових
зсувів. Покладемо
умова
ортогональності (2) порушується і виникає систематична похибка вимірювання фазових
зсувів. Покладемо ![]() і позначимо час інтегрування
і позначимо час інтегрування
![]() , де
, де ![]() дійсне
число. Тоді вирази (3) матимуть вигляд
дійсне
число. Тоді вирази (3) матимуть вигляд
![]() , (5)
, (5)
![]() . (6)
. (6)
Похибка визначення фазових зсувів, яка обумовлена відхиленням інтервалу інтегрування від інтервалу ортогональності (некратність часу інтегрування періоду сигналу) обраховується як
![]() . (7)
. (7)
В формулі
(7) складова ![]() отримана для
отримана для ![]() .
Залежність
.
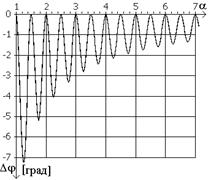
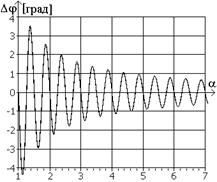
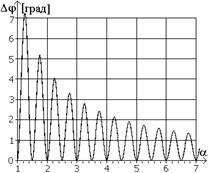
Залежність ![]() для різних значень кута
для різних значень кута ![]() представлені на рис.1а,б,в.
представлені на рис.1а,б,в.
З рис.1
видно, що похибка ![]() може набувати великих
значень. Наприклад, при
може набувати великих
значень. Наприклад, при ![]() , тобто при
, тобто при ![]() похибка дорівнює
похибка дорівнює![]() . Узагальнюючи аналіз цієї складової
похибки
. Узагальнюючи аналіз цієї складової
похибки ![]() можна зробити такі висновки:
можна зробити такі висновки:
·
похибка визначення
фазових зсувв дорівнює ![]() для значень
для значень
![]() , (8)
, (8)
де ![]() , з чого виходить,
що інтервал інтегрування повинен бути кратним часу
, з чого виходить,
що інтервал інтегрування повинен бути кратним часу ![]() ;
;
·
незначне відхилення ![]() від значень
від значень ![]() веде до появи значних похибок, наприклад,
зміна значення
веде до появи значних похибок, наприклад,
зміна значення ![]() =2 на 1% веде до виникнення
похибки
=2 на 1% веде до виникнення
похибки ![]() ;
;
·
похибка набуває
максимальних значень в околі значень ![]() ;
;
·
максимальні значення
похибки зменшуються обернено пропорційно значенню ![]() ;
;
·
похибка залежить
періодично (з періодом ![]() ) від початкової фази сигналу
) від початкової фази сигналу
![]() .
.
|
а) б) в) |
Рис.1 Графіки залежності ![]() для
різних значень фазових зсувів: а)
для
різних значень фазових зсувів: а)![]() , б)
, б) ![]() , в)
, в) ![]()
Таким
чином, при виконанні прецизійних вимірювань фазових зсувів необхідно якомога
точніше задавати тривалість часу спостереження сигналів, яка повинна бути
кратною половині періоду сигналу. Ця вимога стає більш жорсткою при зменшенні
часу спостереження і наближенні до значень (1-2)![]() ,
оскільки однакові абсолютні похибки при визначенні
,
оскільки однакові абсолютні похибки при визначенні ![]() приводять
в цій області до значно більших фазових похибок.
приводять
в цій області до значно більших фазових похибок.
Проведений
вище аналіз вказує на необхідність оцінки періоду сигналу ![]() з метою адаптації часу інтегрування
з метою адаптації часу інтегрування ![]() до
до ![]() , а
при реалізації дискретного ортогонального методу – визначення об’єму вибірки
сигналу
, а
при реалізації дискретного ортогонального методу – визначення об’єму вибірки
сигналу ![]() також адаптованої за значенням
також адаптованої за значенням ![]() .
.
2. Адаптація
об’єму вибірки сигналу до періоду сигналу ![]() .
Дискретний ортогональний спосіб визначення фазових зсувів передбачає виконання
аналого-цифрового перетворення неперервних вхідних сигналів у вибірки їх
значень
.
Дискретний ортогональний спосіб визначення фазових зсувів передбачає виконання
аналого-цифрового перетворення неперервних вхідних сигналів у вибірки їх
значень
![]() ,
, ![]() , (9)
, (9)
де ![]() - об’єм вибірки,
- об’єм вибірки, ![]() - частота дискретизації сигналів, яка
задовільняє теоремі відліків -
- частота дискретизації сигналів, яка
задовільняє теоремі відліків - ![]() (зазвичай
(зазвичай ![]() ). Простим способом узгодження часу
інтегрування з періодом сигналу без зміни частоти дискретизації є коригування
об’єму вибірки, який необхідно обирати з умови
). Простим способом узгодження часу
інтегрування з періодом сигналу без зміни частоти дискретизації є коригування
об’єму вибірки, який необхідно обирати з умови
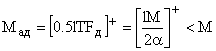 , (10)
, (10)
де ![]() - позначення
операції виділення цілої частини числа. Адаптація об’єму вибірки, яка
відповідає інтервалу ортогональності сигналів (1), виконується за рахунок
зменшення об’єму
- позначення
операції виділення цілої частини числа. Адаптація об’єму вибірки, яка
відповідає інтервалу ортогональності сигналів (1), виконується за рахунок
зменшення об’єму ![]() вихідної вибірки. Найменші
втрати об’єму вибірки мають місце при
вихідної вибірки. Найменші
втрати об’єму вибірки мають місце при ![]() .
З урахуванням цього представимо формулу (10) як
.
З урахуванням цього представимо формулу (10) як![]()
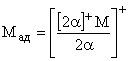 . (11)
. (11)
Отримане
значення ![]() може відрізнятись від точного значення
може відрізнятись від точного значення
![]() на величину
на величину ![]() .
Це значення визначає залишкову похибку оцінки інтервалу інтегрування, отже і
залишкову похибку визначення фазового зсуву. Наприклад, при
.
Це значення визначає залишкову похибку оцінки інтервалу інтегрування, отже і
залишкову похибку визначення фазового зсуву. Наприклад, при ![]() , для всіх
, для всіх ![]() маємо
значення фазової похибки
маємо
значення фазової похибки ![]() .
.
3. Розширення
діапазону вимірювання фазових зсувів. У відповідності до поставленої
задачі необхідно забезпечити однозначне вимірювання фазових зсувів в інтервалі ![]() . Визначення фазових зсувів за відомим
варіантом ортогонального методу, що здійснюється у відповідності з (3)-(5),
забезпечує однозначний результат вимірювань лише в інтервалі
. Визначення фазових зсувів за відомим
варіантом ортогонального методу, що здійснюється у відповідності з (3)-(5),
забезпечує однозначний результат вимірювань лише в інтервалі ![]() . Задачу розширення діапазону можна
вирішити, якщо визначати фазовий зсув кожного з сигналів (1), як його розклад в
системі
. Задачу розширення діапазону можна
вирішити, якщо визначати фазовий зсув кожного з сигналів (1), як його розклад в
системі ![]() , компоненти якої можуть бути
некогерентними сигналам (1). Така можливість існує з огляду на те, що,
по-перше, формування таких квадратурних компонент здійснюється в цифровій
формі, по-друге, період вимірювального сигналу, і частота дискретизації є
величини відомі. Синтез вибірок квадратурних компонент опорного коливання здійснюється
за формулами
, компоненти якої можуть бути
некогерентними сигналам (1). Така можливість існує з огляду на те, що,
по-перше, формування таких квадратурних компонент здійснюється в цифровій
формі, по-друге, період вимірювального сигналу, і частота дискретизації є
величини відомі. Синтез вибірок квадратурних компонент опорного коливання здійснюється
за формулами
![]() (12)
(12)
Тоді квадратурні компоненти першого сигналу (1) в цифровій формі визначаються як
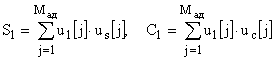 , (13)
, (13)
для другого сигналу (1) –
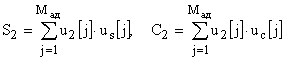 . (14)
. (14)
Отримавши квадратурні компоненти (13), (14) можна у
відповідності до загальної формули (4) визначити окремо значення ![]() і
і ![]() ,
отже і їх різницю
,
отже і їх різницю ![]() .
.
Використання некогерентного опорного сигналу має і
іншу важливу перевагу – в цьому разі немає потреби у виконанні в інтервалі
частот![]() прецизійного зсуву сигналу на кут
прецизійного зсуву сигналу на кут ![]() , що необхідно при обрахунку
квадратурних компонент за формулами (3), і що є досить складним технічним
завданням. Крім того, система з некогерентними опорними сигналами зберігатиме
працездатність при наявності адитивних шумових складових в обох вимірювальних
сигналах.
, що необхідно при обрахунку
квадратурних компонент за формулами (3), і що є досить складним технічним
завданням. Крім того, система з некогерентними опорними сигналами зберігатиме
працездатність при наявності адитивних шумових складових в обох вимірювальних
сигналах.
4.Усереднення результатів вимірювань фазових зсувів. В умовах дії завад поточні значення різниці фазових
зсувів мають суттєву випадкову похибку, яка може бути зменшена за рахунок
усереднення. Для об’єму ![]() , усереднюваних
фазових зсувів, які утворюють вектор
, усереднюваних
фазових зсувів, які утворюють вектор ![]() , усереднення і
отримання результата в інтервалі
, усереднення і
отримання результата в інтервалі ![]() виконується у
відповідності до алгоритму усереднення на колі [8]
виконується у
відповідності до алгоритму усереднення на колі [8]
![]() , (15)
, (15)
де
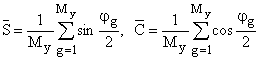 . (16)
. (16)
5. Застосування пакета LabVIEW. Розробка системи виконувалось із застосуванням програмного пакета LabVIEW версії 6, розробленої фірмою National Instruments (США) – одного зі світових лідерів в розробці програмного і апаратного забезпечення інформаційно-вимірювальних систем [9]. Пакет LabVIEW має широку бібліотеку програмних модулів для генерації та обробки сигналів і надає розробнику зручний інструмент побудови вимірювальних приладів, дозволяючи поєднати первинні вимірювальні перетворювачі, аналого-цифрові та цифро-аналогові перетворювачі і програмні засоби, які здатні реалізувати функції різноманітних вимірювальних приладів в єдину інформаційно-вимірювальну систему.
Мова LabVIEW за своєю структурою наближається до мов програмування СІ та Бейсік. Однак вона не потребує написання текстів програм – в LabVIEW використовується графічне програмування, за допомогою якого і створюються програми у вигляді блок-схем.
Інтерактивний інтерфейс розроблених в LabVIEW приладів уявляє собою графічне зображення передніх панелей фізичних приладів і дозволяє імітувати роботу всіх органів управління та пристроїв, які відповідають фізичному приладу.
6. Реалізація автоматизованої системи вимірювання фазових характеристик. Структура автоматизованої системи вимірювання фазових характеристик періодичних сигналів за методом дискретної ортогональної обробки і синтезом некогерентного опорного сигналу наведена на рис.2.
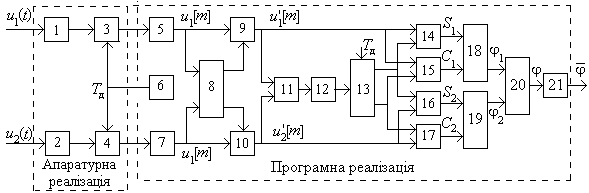
Рис.2 Структура автоматизованої фазовимірювальної системи з дискретною ортогональною обробкою сигналів
На рис.1. позначено: 1,2 – вхідні пристрої, 3,4, - аналого-цифрові перетворювачі, 5,7 – оперативні запам’ятовувальні пристрої, 6 – генератор сигналів дискретизації, 8 – блоки попереднього аналізу спектра сигналів, 9,10 – цифрові фільтри, 11 – блок визначення періоду, 12 – блок адаптації об’єму вибірки, 13 – формувач копії сигналу, 14-17 – обчислювачі квадратурних компонент, 18,19 – обчислювачі функції arctg, 20 – віднімач, 21 –блок усереднення.
Вхідні пристрої 1,2 узгоджують вхідні ланцюги
системи з джерелами сигналів. Аналогово-цифрові перетворювачі 3,4 формують
вибірки вхідних сигналів (9). Блоки 1-4 реалізуються у вигляді окремої плати
введення/виведення аналогових сигналів, яка конструктивно розміщується на
материнській платі ПК. Вибіркою даних керує пристрій 6. Потоки відліків вхідних
сигналів ![]() надходять, відповідно, на оперативні запам’ятовувальні
пристрої 5,7, розраховані на об’єми вибірок
надходять, відповідно, на оперативні запам’ятовувальні
пристрої 5,7, розраховані на об’єми вибірок ![]() . Пристрій 8 здійснює попередній спектральний
аналіз і керує цифровими фільтрами 9,10 [10], які вилучають з сигналів, в разі
наявності, зосереджені завади, оскільки фазометри з ортогональною обробкою
чутливі до завад такого типу. Необхідність такої обробки обумовлена тим, що оптимальні
по відношенню до білого гауссівського шуму ортогональні фазометри мають низьку
завадостійкість до зосереджених завад. В роботі [6] запропонована вагова обробка
сигналів для зменшення впливу завад такого типу. Проте разом з цим збільшується
похибка від дії гауссівської завади. Застосування перестроюваних цифрових
фільтрів розв’язує це протиріччя. Введення в структуру системи цифрових
фільтрів дозволяє вирішити і інші задачі побудови ІВС – задачу прецизійного
вимірювання фазових характеристик полігармонічних сигналів, сигналів зі значним
рівнем нелінійних спотворень, тощо.
. Пристрій 8 здійснює попередній спектральний
аналіз і керує цифровими фільтрами 9,10 [10], які вилучають з сигналів, в разі
наявності, зосереджені завади, оскільки фазометри з ортогональною обробкою
чутливі до завад такого типу. Необхідність такої обробки обумовлена тим, що оптимальні
по відношенню до білого гауссівського шуму ортогональні фазометри мають низьку
завадостійкість до зосереджених завад. В роботі [6] запропонована вагова обробка
сигналів для зменшення впливу завад такого типу. Проте разом з цим збільшується
похибка від дії гауссівської завади. Застосування перестроюваних цифрових
фільтрів розв’язує це протиріччя. Введення в структуру системи цифрових
фільтрів дозволяє вирішити і інші задачі побудови ІВС – задачу прецизійного
вимірювання фазових характеристик полігармонічних сигналів, сигналів зі значним
рівнем нелінійних спотворень, тощо.
З метою зменшення похибки (7) в структуру рис.2
введено блоки 11,12, які узгоджують об’єм вибірки сигналів з його періодом.
Синтез вибірок квадратурних компонент (12) опорного сигналу здійснюється блоком
13. Обчислювачі квадратурних компонент 14-17 виконують операції перемноження та
підсумовування (13), (14) і формують квадратурні складові ![]() . Обчислювачі 18,19 функції арктангенса
визначають, у відповідності до (4), фазові зсуви
. Обчислювачі 18,19 функції арктангенса
визначають, у відповідності до (4), фазові зсуви ![]() вхідних сигналів відносно синтезованих опорних сигналів з нульовими
початковими фазовими зсувами. Поточні
значення різниці фазових зсувів
вхідних сигналів відносно синтезованих опорних сигналів з нульовими
початковими фазовими зсувами. Поточні
значення різниці фазових зсувів ![]() визначає віднімач
20, а усереднення поточних значень на колі у відповідності з формулами (15),
(16) виконує пристрій усереднення 21.
визначає віднімач
20, а усереднення поточних значень на колі у відповідності з формулами (15),
(16) виконує пристрій усереднення 21.
Програма обробки сигналів у відповідності до структури рис.2, елементи управління системою та режимами візуалізації проміжних та кінцевих результатів вимірювання виконані в системі LabVIEW, яка дозволяє також створити зручний інтерфейс користувача і підтримувати інтерактивний режим роботи. Зовнішній вигляд інтерфейсу представлено на рис. 3.

Рис.3 Інтерфейс автоматизованої фазової ІВС, створений в системі LabVIEW
Інтерфейс має чотири вікна, на яких зображено вхідні
сигнали (перше і друге вікна), похибка вимірювання фазового зсуву без
усереднення (третє вікно) і з усередненням при ![]() (четверте
вікно) для випадку вимірювання фазового зсуву
(четверте
вікно) для випадку вимірювання фазового зсуву ![]() . Значення
похибок у третьому і четвертому вікнах наведені для випадків, коли адаптація
об’єму вибірки відсутня (початок графіків) і з адаптацією (прикінцева частина
графіків).
. Значення
похибок у третьому і четвертому вікнах наведені для випадків, коли адаптація
об’єму вибірки відсутня (початок графіків) і з адаптацією (прикінцева частина
графіків).
Введення аналогових сигналів в ПК здійснювалось за
допомогою плати введення/виведення серії 1800 фірми ICCP DAS (шина PCI, ![]() < 330 кГц, комутатор на 8 каналів,
12-розрядний аналого-цифровий перетворювач). Застосування цієї плати дозволяє
виконувати вимірювання в діапазоні
< 330 кГц, комутатор на 8 каналів,
12-розрядний аналого-цифровий перетворювач). Застосування цієї плати дозволяє
виконувати вимірювання в діапазоні ![]() Гц. Графічний
інтерфейс, програма управління процесом вимірювання та обчислення реалізовані в
системі LabVIEW.
Гц. Графічний
інтерфейс, програма управління процесом вимірювання та обчислення реалізовані в
системі LabVIEW.
Запропонована реалізація фазової ІВС забезпечує
розв’язок існуючих (перелічених вище) проблем. Так, розширення діапазону
вимірювання до інтервалу ![]() та вилучення зі
структури прецизійного широкосмугового фазообертача відбулося за рахунок застосування
в ІВС некогерентного опорного сигналу, зменшення впливу зосереджених завад – за
рахунок використання цифрової фільтрації, а зменшення похибки від некратності
часу інтегрування періоду сигналу для широкої смуги частот – оцінкою періоду
вимірювальних сигналів та адаптацією об’єму вибірки.
та вилучення зі
структури прецизійного широкосмугового фазообертача відбулося за рахунок застосування
в ІВС некогерентного опорного сигналу, зменшення впливу зосереджених завад – за
рахунок використання цифрової фільтрації, а зменшення похибки від некратності
часу інтегрування періоду сигналу для широкої смуги частот – оцінкою періоду
вимірювальних сигналів та адаптацією об’єму вибірки.
В даній реалізації частотний діапазон системи обмежений лише швидкодією плати введення/виведення. Її заміна на більш високочастотну не потребує модернізації програми. Крім того слід сказати, що сучасні швидкісні АЦП, які встановлюються на платах введення/виведення мають пристрої вибірки та збереження, що дозволяє, при потребі, реалізувати стробоскопічний режим роботи системи, за рахунок чого суттєво розширюється частотний діапазон системи.
Таким чином, на прикладі розглянутої ІВС показано, що система LabVIEW в комплексі з платою введення/виведення та ПК дозволяє розробляти в стислі терміни складні ІВС з заданими характеристиками, властивості яких можуть бути досліджені.
Висновки
Результати досліджень дають можливість обґрунтувати застосування у фазових ІВС новітніх інформаційних технологій на базі цифрової обробки сигналів, що дозволяє покращити метрологічні характеристики ІВС, а саме збільшити динамічний діапазон сигналів, скоротити час вимірювання, зменшити похибки вимірювання фазових зсувів сигналів при співвідношеннях сигнал/завада в околі одиниці, розширити область їх застосування та скоротити час проектування систем.
Отриманий аналітичний вираз (7) похибки фазометрів з дискретною ортогональною обробкою сигналів в залежності від тривалості часу інтегрування дозволяє обрахувати ці похибки для різних інтервалів спостереження сигналів і сформувати обґрунтовані рекомендації по їх зменшенню шляхом адаптації об’єму вибірки сигналів до їх періоду.
Виконана із застосуванням технології LabVIEW модель фазової ІВС дозволяє не тільки здійснювати технічні вимірювання, але й проводити дослідження різних режимів роботи системи, визначення складових похибки при проведенні імітаційного модельного експерименту.
Діапазон
вимірювання фазових зсувів запропонований ІВС порівняно з традиційними
приладами та системами збільшений вдвічі і становить ![]() .
.
The realization of phase measuring system with using of LabVEIW technology is offered and its features of functioning are considered. The analysis of new variants of the phase measuring system with discrete orthogonal signal processing are carried out. The error of the phase characteristics measurement is determined at the limited time signal processing.
1. Беляевский Л.С., Новиков В.С, Олянюк П.В. Основы радионавигации: Учебник для вузов гражд. Авиации.- М.: Транспорт, 1982. – 288 с.
2. Лобачев В.М. Радиоэлектронная геодезия.- М.: Недра, 1980.- 327 с.
3. Пестряков В.Б. Фазовые радиотехнические системы (Основы статистической теории) - М.: Сов. радио, 1968. - 466 с.
4. Кинкулькин И.Е., Рубцов В.Д., Фабрик М.А. Фазовый метод определения координат.- М.: Сов.радио, 1979.- 280 с.
5. Маєвський С.М., Куц Ю.В. Гетеродинна інтерференційна система контролю якості дзеркал // Автоматизація фізичних методів контр. в технічній діагностиці та медицині. Тези.доп. школи-семінару 12-14вер.1995р.,м.Славське Львівської обл., с.19.
6. Бабак В.П., Куц Ю.В. Метод однозначного визначення великих фазових зсувів сигналів // Вісник НАУ.-2003.-№1.-С.3-8.
7. Чмых М.К. Цифровая фазометрия. – М.: Радио и связь, 1993.- 184 с.
8. Мардиа К. Статистический анализ угловых наблюдений.- М.: Наука, Гл.ред.физ.-мат.лит., 1978.- 240 с.
9. Жарков Ф.П., Каратаев В.В. и др. Использование виртуальных инструментов LabVIEW. М.: Солон-Р, Радио и связь, 1999. – 268с.
10. Бабак В.П. та ін. Обробка сигналів: Підручник/ В.П. Бабак, В.С. Хандецький, Е. Шрюфер. – К.: Либідь, 1999.- 496 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Информационно-измерительные системы
Ковальов О.І. Вимірювання у процесно-орієнтованих стандартахПолякова М.В., Ищенко А.В., Худайбердин Э.И. Порогово-пространственная сегментация цветных текстурированных изображений на основе метода JSEG
Дзюбаненко А. В. Организация компьютерных систем для анализа изображений
Гордеев Б.Н., Зивенко А.В., Наконечный А.Г. Формирование зондирующих импульсов для полиметрических измерительных систем
Богданов А.В., Бень А.П., Хойна С.И. Релаксация обратного тока диодов Шоттки после их магнитно-импульсной обработки (МИО)
Тверезовский В.С., Бараненко Р.В. Проектирование измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Оптимизированная модель измерителя доб-ротности варикапов
Руднєва М.С., Кочеткова О.В., Задорожній Р.О. Принципи побудови оптимальної структури інформаційно-вимірювальної системи геометричних розмірів об’єктів в діапазоні від 1 нм до 1000 нм
Биленко М.С., Рожков С.А., Единович М.Б. Идентификация деформаций пе-риодических структур с использованием систем технического зрения
Рашкевич Ю.М., Ковальчук А.М., Пелешко Д.Д. Афінні перетворення в модифікаціях алгоритму RSA шифрування зображень
Дидык А.А., Фефелов А.А, Литвиненко В.И., Шкурдода С.В., Синяков Ф. В. Классификация масс-спектров с помощью кооперативного иммунного алгоритма
Клименко А.K. Обратная модель для решения задач в системах с многосвязными динамическими объектами
Завгородній А.Б. Порівняльне дослідження твердотільних і рідиннофазних об'єктів методом газорозрядної візуалізації
Голощапов С.С., Петровский А.В., Рожко Ж.А., Боярчук А.И. Измерение доб-ротности колебательного контура на основе метода биения частот
Кириллов О.Л., Якимчук Г.С. Диагностирование критерия безопасности при заполнении замкнутых объемов СПЖ косвенным методом
Долина В.Г. Проблеми підвищення точності рефрактометра на основі прозорих порожнистих циліндрів.
Самков О.В., Захарченко Ю.А. Застосування алгоритму клонального відбору для побудови планів модернізації авіаційної техніки
Попов Д.В. Метод формування регламентів технічного обслуговування повітряних суден
Казак В.М., Чорний Г.П., Чорний Т.Г. Оцінювання готовності технічних об’єктів з урахуванням достовірності їх контролю
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования цифрового измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования устройства для разбраковки варикапов по емкостным параметрaм и добротности
Сосюк А.В. Інтелектуальний автоматизований контроль знань в системах дистанційного навчання
Соколов А.Є. Деякі аспекти систезу комп’ютеризованої адаптивної системи навчання
Полякова М.В., Волкова Н.П., Іванова О.В. Сегментація зображень стохастичних текстур амплітудно-детекторним методом у просторі вейвлет-перетворення
Луцкий М.Г., Пономаренко А.В., Филоненко С.Ф. Обработка сигналов акустической эмиссии при определении положения сквозных дефектов
Литвиненко В.И., Дидык А.А., Захарченко Ю.А. Компьютерная система для решения задач классификации на основе модифицированных иммунных алгоритмов
Лубяный В.З., Голощапов С.С. Прямоотсчетные измерители расхождений емкостей
Беляев А.В. Построение навигации для иерархических структур в WEB-системах и системах управления WEB-сайтом
Терновая Т.И., Сумская О.П., Слободянюк И.И., Булка Т.И. Контроль качества тканей специального назначения с помощью автоматических систем.
Шеховцов А.В. Інформаційний аспект: розпізнавання образів індивідуума.
Полякова М.В. Определение границ сегмента упорядоченной текстуры на изображении с однородным фоном с помощью многоканального обнаружения пачки импульсов.
Литвиненко В.И. Прогнозирования нестационарных временных рядов с помощью синтезируемых нечетких нейронных сетей
Ковриго Ю.М., Мисак В.Ф., Мовчан А.П., Любицький С.В. Автоматизована система діагностики генераторів електростанцій
Браїловський В.В., Іванчук М.М., Ватаманюк П.П., Танасюк В.С. Керований детектор імпульсного ЯКР спектрометра
Забытовская О.И. Построение функции полезности по экспериментальным данным.
Шиманські З. Апаратні засоби сегментації мовного сигналу
Хобин В.А., Титлова О.А. К вопросу измерения парожидкостного фронта в дефлегматоре абсорбционно-диффузионной холодильной машины (АДХМ)
Фефелов А. А. Использование байесовских сетей для решения задачи поиска места и типа отказа сложной технической системы
Слань Ю. М., Трегуб В. Г. Оперативна нейромережна ідентифікація складних об’єктів керування
Ролик А.И. Модель управления перераспределением ресурсов информационно-телекоммуникационной системы при изменении значимости бизнес-процессов
Кириллов О.Л., Якимчук Г.С., Якимчук С.Г. Изучение электрического поля с помощью датчика измерителя электростатического потенциала на модели замкнутого металлического объема
Грицик В.В. Застосування штучних нейронних мереж при проектуванні комп’ютерного зору.
Гасанов А.С. Информационные технологии построения систем прогнозирования отказов
Шеховцов А.В., Везумский А.К., Середа Е.С. Алгоритм сжатия информации без потерь: модифицированный алгоритм LZ77
Ходаков В.Е., Жарикова М.В., Ляшенко Е.Н. Методы и алгоритмы визуализации пространственных данных на примере моделирования распространения лесных пожаров.
Полякова М.В., Крылов В.Н. Обобщённые масштабные функции с компактным носителем в задаче сегментации изображений упорядоченных текстур. – C. 75 – 84.
Полторак В.П., Дорогой Я.Ю. Система распознавания образов на базе нечеткого нейронного классификатора.
Литвиненко В.И. Синтез радиально-базисных сетей для решения задачи дистанционного определения концентрации хлорофилла.
Бражник Д.А. Управление совмещением изображения объекта в сцене и эталонного изображения.
Бабак В.П., Пономаренко А.В. Локализация места положения сквозных дефектов по сигналам акустической эмиссии.
Мороз В. В. R-D проблема и эффективность систем сжатия изображений.
Крылов В.Н., Полякова М.В., Волкова Н.П. Контурная сегментация в пространстве гиперболического вейвлет-преобразования с использованием математической морфологии.
Квасников В.П., Баранов А.Г. Анализ влияния дестабилизирующих факторов на работу биканальной координатно-измерительной машины.
Казак В.М., Гальченко С.М., Завгородній С.О. Аналіз можливості застосування імовірнісних методів розпізнавання для виявлення пошкоджень зовнішнього обводу літака.
Тищенко И.А., Лубяный В.З. Управление коммутационными процессами в интегрированных сетях связи.
Корниенко-Мифтахова И.К.,Филоненко С.Ф. Информационно-измерительная система для анализа характеристик динамического поведения конструкций.
Тверезовский В.С., Бараненко Р.В. Модель измерителя емкости с линейной шкалой измерений.
Полякова М.В., Крылов В.Н. Мультифрактальный метод автоматизированного распознавания помех на изображении.
Рожков С.О., Федотова О.М. Алгоритм розпізнавання дефектів тканин для автоматичної системи контролю якості.
Бражник Д.А. Использование проективного преобразования для автоматизации обнаружения объектов.