УДК 62-50
АНАЛІЗ ЕФЕКТИВНОСТІ ФУНКЦІОНУВАННЯ МЕРЕЖІ БАЙЄСА
Бідюк П.І., Литвиненко В.І., Кроптя А.В.
Мережа Байєса (МБ) – це ймовірнісна графічна модель причинних зв’язків між якісними та кількісними змінними, яка створюється для описання статики або динаміки об’єктів різної природи з метою формування висновку щодо того чи іншого (поточного) стану досліджуваного об’єкта. Будь-яка нова інформація щодо об’єкта використовується для оновлення розподілів ймовірностей станів, які характеризуються вузловими змінними мережі. На основі оновлених розподілів ймовірностей формується статистичний висновок, який дає можливість особі, що приймає рішення (ОПР), прийняти рішення щодо виконання відповідних дій. Перевагою мереж Байєса у порівнянні з іншими підходами до врахування та обробки невизначеностей різної природи є достатня формалізація всіх етапів їх побудови та використання.
Байєсові мережі знаходять все ширше застосування в обробці статистичних, даних, представлених часовими рядами і часовими перерізами, а також якісними даними, представленими експертними оцінками, лінгвістичними змінними і т. ін. Судячи з числа публікацій, саме широке застосування БМ знайшли у розв’язку задач медичної діагностики, де вони допомагають ставити та уточнювати діагнози самих різних хвороб в умовах неточної та неповної інформації [1-8]. Відомі застосування БМ в системах технічної діагностики – система моніторингу космічного корабля багаторазового використання, діагностика двигунів різного призначення, аналіз стану технологічних процесів та технічних систем [9-12]. Широке застосування знаходять БМ в системах класифікації даних різної природи [13], системах автоматичного розпізнавання мовних сигналів [14], маркетингу і бізнесі [15, 16], а також у багатьох інших сферах діяльності [17, 18]. Загалом БМ дає можливість відтворити причинно-наслідкові зв’язки між подіями та визначити ймовірності настання тієї чи іншої ситуації при отриманні нової інформації (свідчення) щодо зміни стану будь-якого вузла (змінної) мережі. Ступінь успішності застосування даного методу моделювання та формування статистичного висновку залежить від вміння коректно сформулювати постановку задачі, вибрати змінні процесу, які в достатній мірі характеризують його динаміку або статику, зібрати статистичні дані та використати їх для навчання мережі, а також коректно сформувати результат – висновок за допомогою побудованої мережі.
Оскільки МБ – це допоміжний інструмент при прийнятті рішень, то виникає питання щодо його ефективності і як змінюється його ефективність в часі? Невизначеності, притаманні окремим змінним та групам змінних МБ, стають ключовими факторами впливу на рішення, що приймаються за участю МБ. Розглянемо міру невизначеності, зв’язану з деякою випадковою змінною, яка є елементом МБ.
Постановка задачі
Метою даної роботи є:
– виконання аналізу ефективності функціонування мереж Байєса в загальному випадку;
– встановлення можливості побудови кількісного критерію для оцінювання міри невизначеності, яка може бути описана за допомогою МБ.
Розв’язання задачі
Формально, БМ – це графічна модель процесу, яка визначається трійкою ![]() , першою компонентою якої є множина змінних
, першою компонентою якої є множина змінних ![]() ; другою – спрямований ациклічний граф
; другою – спрямований ациклічний граф ![]() , вузли якого відповідають випадковим змінним модельованого процесу;
, вузли якого відповідають випадковим змінним модельованого процесу; ![]() спільний розподіл ймовірностей змінних
спільний розподіл ймовірностей змінних ![]() . При цьому стосовно множини змінних виконується марковська умова, тобто кожна змінна мережі не залежить від усіх інших змінних, за винятком батьківських попередників цієї змінної.
. При цьому стосовно множини змінних виконується марковська умова, тобто кожна змінна мережі не залежить від усіх інших змінних, за винятком батьківських попередників цієї змінної.
Нехай ![]() дискретна змінна, яка приймає конкретні значення з ймовірностями
дискретна змінна, яка приймає конкретні значення з ймовірностями ![]() . У відповідності до байєсівської інтерпретації будемо розглядати так звані суб’єктивні ймовірності, тобто ймовірність, як міру довіри, що грунтується на наших поточних знаннях про процес чи об’єкт. Однак, цих знань може виявитись недостатньо для формування альтернативи при прийнятті рішення, тобто виникає поточна ситуативна невизначеність. Міру цієї невизначеності можна сформулювати так: „мірою поточної невизначеності є об’єм інформації, який необхідно додати до наявної поточної інформації (знань) про процес з метою ідентифікації конкретної альтернативи щодо прийняття рішення.”
. У відповідності до байєсівської інтерпретації будемо розглядати так звані суб’єктивні ймовірності, тобто ймовірність, як міру довіри, що грунтується на наших поточних знаннях про процес чи об’єкт. Однак, цих знань може виявитись недостатньо для формування альтернативи при прийнятті рішення, тобто виникає поточна ситуативна невизначеність. Міру цієї невизначеності можна сформулювати так: „мірою поточної невизначеності є об’єм інформації, який необхідно додати до наявної поточної інформації (знань) про процес з метою ідентифікації конкретної альтернативи щодо прийняття рішення.”
Тобто для визначення конкретної альтернативи при прийнятті рішення необхідно провести додатковий експеримент з метою отримання необхідної інформації. В такому випадку за міру невизначеності можна прийняти число можливих альтернатив та відповідний розподіл ймовірностей ![]() . Усереднену невизначеність, зв’язану з випадковою змінною
. Усереднену невизначеність, зв’язану з випадковою змінною ![]() , можна оцінити за допомогою ентропії Шеннона
, можна оцінити за допомогою ентропії Шеннона
![]() . (1)
. (1)
Якщо за основу логарифму прийняти 2, то одиницею виміру ентропії буде один біт, що зручно для аналізу. У випадку повної інформації про процес, наприклад, відомо, що ![]() і
і ![]() , отримаємо:
, отримаємо: ![]() . Якщо ж поточна інформація про об’єкт є повністю невизначеною, тобто значення змінної
. Якщо ж поточна інформація про об’єкт є повністю невизначеною, тобто значення змінної ![]() мають рівномірний розподіл,
мають рівномірний розподіл, ![]() , то вибрати одну альтернативу з множини допустимих неможливо. У цьому випадку
, то вибрати одну альтернативу з множини допустимих неможливо. У цьому випадку ![]() приймає максимальне значення:
приймає максимальне значення:
![]() .
.
Тому в загальному випадку можна прийняти, що ![]() є мірою інформації, необхідної для подолання невизначеності, яка визначається розподілом ймовірності
є мірою інформації, необхідної для подолання невизначеності, яка визначається розподілом ймовірності ![]() .
.
З іншого боку ![]() можна розглядати як міру розсіювання розподілу
можна розглядати як міру розсіювання розподілу ![]() , тобто концепція ентропії відіграє таку ж роль, як дисперсія у статистиці. Однак
, тобто концепція ентропії відіграє таку ж роль, як дисперсія у статистиці. Однак ![]() має більш загальне призначення ніж дисперсія, оскільки змінна
має більш загальне призначення ніж дисперсія, оскільки змінна ![]() може приймати кількісні та якісні (лінгвістичні) значення.
може приймати кількісні та якісні (лінгвістичні) значення.
В МБ ймовірності (ступінь довіри) розповсюджуються від інформаційних змінних до змінних, щодо яких формулюються гіпотези, що дає можливість розглядати БМ як множину „інформаційних каналів”. Якщо прийняти таку концепцію МБ, це дасть можливість використати результати теорії інформації при аналізі невизначеностей. Оскільки інформація розповсюджується в МБ у відповідності до теореми Байєса, то запишемо результат, який має таке ж значення для ентропії, як і теорема Байєса для ймовірностей. Так, спільна ентропія для двох випадкових змінних ![]() і
і ![]() задовольняє співвідношенню:
задовольняє співвідношенню:
![]() , (2)
, (2)
де ![]() умовна ентропія змінної
умовна ентропія змінної ![]() по відношенню до
по відношенню до ![]() , яка визначається за виразом:
, яка визначається за виразом:
![]() . (3)
. (3)
З властивості комутативності кон’юнкції ![]() , тобто
, тобто ![]() , випливає, що:
, випливає, що:
![]() . (4)
. (4)
Згідно з прийнятою концепцією ![]() представляє апріорну невизначеність щодо
представляє апріорну невизначеність щодо ![]() , тобто невизначеність знання щодо змінної
, тобто невизначеність знання щодо змінної ![]() при відсутності іншої інформації, а
при відсутності іншої інформації, а ![]() – апостеріорна невизначеність щодо
– апостеріорна невизначеність щодо ![]() при умові, що
при умові, що ![]() прийняла деяке значення. Таким чином, (4) вказує на зв’язок між апріорною та апостеріорною ентропією; можна показати , що:
прийняла деяке значення. Таким чином, (4) вказує на зв’язок між апріорною та апостеріорною ентропією; можна показати , що:
![]() . (5)
. (5)
Рівність у (5) можлива тільки у випадку, коли ![]() і
і ![]() повністю незалежні. Можна стверджувати, що розповсюдження ймовірностей (довіри) по мережі в середньому приводить до зменшення ентропії. Однак, справедливість цього твердження у середньому означає, що
повністю незалежні. Можна стверджувати, що розповсюдження ймовірностей (довіри) по мережі в середньому приводить до зменшення ентропії. Однак, справедливість цього твердження у середньому означає, що ![]() не завжди буде меншою
не завжди буде меншою ![]() ; можливі випадки, коли
; можливі випадки, коли ![]() . Іншими словами, отримання нової інформації може призвести до зростання невизначеності (наприклад, при оцінюванні типу ситуації), але в середньому нова інформація завжди зменшує ступінь невизначеності.
. Іншими словами, отримання нової інформації може призвести до зростання невизначеності (наприклад, при оцінюванні типу ситуації), але в середньому нова інформація завжди зменшує ступінь невизначеності.
Аналіз впливу нової інформації на змінну, щодо якої формулюється гіпотеза
Нехай МБ містить змінну ![]() , відносно якої формулюється гіпотеза, та інформаційну змінну
, відносно якої формулюється гіпотеза, та інформаційну змінну ![]() . При появі нового значення
. При появі нового значення ![]() інформація розповсюджується по мережі, що приводить до зміни розподілу
інформація розповсюджується по мережі, що приводить до зміни розподілу ![]() на
на ![]() . Ентропія змінної
. Ентропія змінної ![]() стає рівною
стає рівною ![]() . Напрям зміни цієї ентропії залежить від наступних факторів: (1) значення апріорних ймовірностей
. Напрям зміни цієї ентропії залежить від наступних факторів: (1) значення апріорних ймовірностей ![]() ; (2) рівня знань, накопичених у МБ в термінах умовних ймовірностей (ці умовні ймовірності відіграють ключову роль у формуванні висновку на основі МБ). Постає питання визначення ефективності механізму формування висновку у МБ щодо зменшення невизначеності за допомогою нової інформації. Це можна зробити, якщо відокремити вплив апріорних ймовірностей від механізму формування висновку. Один із простих підходів до розв’язання цієї задачі полягає у тому, що припускається відсутність апріорної інформації відносно ключової змінної, щодо якої формулюється гіпотеза. Це дає можливість встановити ступінь впливу нової інформації на початкову невизначеність.
; (2) рівня знань, накопичених у МБ в термінах умовних ймовірностей (ці умовні ймовірності відіграють ключову роль у формуванні висновку на основі МБ). Постає питання визначення ефективності механізму формування висновку у МБ щодо зменшення невизначеності за допомогою нової інформації. Це можна зробити, якщо відокремити вплив апріорних ймовірностей від механізму формування висновку. Один із простих підходів до розв’язання цієї задачі полягає у тому, що припускається відсутність апріорної інформації відносно ключової змінної, щодо якої формулюється гіпотеза. Це дає можливість встановити ступінь впливу нової інформації на початкову невизначеність.
Якщо інформація щодо ключову змінну ![]() відсутня, то за принципом максимальної ентропії
відсутня, то за принципом максимальної ентропії ![]() , а апріорна ентропія складає
, а апріорна ентропія складає ![]() . При надходженні інформації
. При надходженні інформації ![]() ентропія зменшується на величину:
ентропія зменшується на величину:
![]() . (6)
. (6)
Апостеріорні ймовірності ![]() розраховуються на основі апріорних ймовірностей
розраховуються на основі апріорних ймовірностей ![]() . Оскільки
. Оскільки ![]() – максимально можлива ентропія, то вираз (6) завжди додатній. В зв’язку з цим вираз (6) можна назвати ступінню редукції невизначеності за рахунок інформації
– максимально можлива ентропія, то вираз (6) завжди додатній. В зв’язку з цим вираз (6) можна назвати ступінню редукції невизначеності за рахунок інформації ![]() . Якщо
. Якщо ![]() – нова інформація, яка представлена декількома значеннями
– нова інформація, яка представлена декількома значеннями ![]() , отриманими з різних джерел, то ступінь зменшення невизначеності можна визначити як
, отриманими з різних джерел, то ступінь зменшення невизначеності можна визначити як
![]() .
.
Аналіз задачі оцінювання зменшення невизначеності при надходженні нової інформації в межах мережі Байєса приводить до трьох наступних випадків:
1. Нехай ![]() коренева змінна і по відношенню до неї формулюється гіпотеза. Присвоїмо цій та іншим кореневим змінним розподіл, який забезпечує однакову ймовірність появи всіх можливих значень. Після досягнення мережею рівноваги при таких початкових умовах одній або більше інформаційним змінним задамо відповідне значення. Апостеріорні ймовірності
коренева змінна і по відношенню до неї формулюється гіпотеза. Присвоїмо цій та іншим кореневим змінним розподіл, який забезпечує однакову ймовірність появи всіх можливих значень. Після досягнення мережею рівноваги при таких початкових умовах одній або більше інформаційним змінним задамо відповідне значення. Апостеріорні ймовірності ![]() розрахуємо після того, як мережа знову досягне стану рівноваги. Ступінь зменшення невизначеності завдяки появі нової інформації можна обчислити на основі апріорних та апостеріорних ймовірностей.
розрахуємо після того, як мережа знову досягне стану рівноваги. Ступінь зменшення невизначеності завдяки появі нової інформації можна обчислити на основі апріорних та апостеріорних ймовірностей.
2. Якщо змінна ![]() , по відношенню до якої формулюється гіпотеза, не коренева, то вилучаємо з мережі її батьківські вузли (змінні) і реалізуємо процедуру, описану в п. 1.
, по відношенню до якої формулюється гіпотеза, не коренева, то вилучаємо з мережі її батьківські вузли (змінні) і реалізуємо процедуру, описану в п. 1.
3. Можлива ситуація, коли нова інформація впливає на ![]() через один з її батьківських вузлів, наприклад
через один з її батьківських вузлів, наприклад ![]() . В такому випадку вилучення батьківських вузлів призведе до виникнення розриву на шляху розповсюдження нової інформації до
. В такому випадку вилучення батьківських вузлів призведе до виникнення розриву на шляху розповсюдження нової інформації до ![]() . Оскільки нова інформація впливає безпосередньо на
. Оскільки нова інформація впливає безпосередньо на ![]() і тільки опосередковано впливає на
і тільки опосередковано впливає на ![]() , то будемо вважати
, то будемо вважати ![]() первинною змінною, щодо якої формулюється гіпотеза, і будемо розглядати її апріорні ймовірності замість
первинною змінною, щодо якої формулюється гіпотеза, і будемо розглядати її апріорні ймовірності замість ![]() . Іншими словами, якщо
. Іншими словами, якщо ![]() – коренева змінна, то ми розглядаємо всі її стани як рівноймовірні (як у першому випадку), а якщо
– коренева змінна, то ми розглядаємо всі її стани як рівноймовірні (як у першому випадку), а якщо ![]() – не коренева змінна, то поступаємо так, як у другому випадку. Оскільки
– не коренева змінна, то поступаємо так, як у другому випадку. Оскільки ![]() – батьківська змінна для
– батьківська змінна для ![]() , то встановлення апріорних ймовірностей для
, то встановлення апріорних ймовірностей для ![]() автоматично приведе до встановлення апріорних ймовірностей для
автоматично приведе до встановлення апріорних ймовірностей для ![]() .
.
Приклад розрахунку ймовірностей. Розглянемо МБ, побудовану для розв’язання задачі ситуаційного аналізу. За цільову змінну, щодо якої формулюється гіпотеза, виберемо змінну „активність”. Розрахуємо ступінь зменшення невизначеності щодо змінної діяльність з надходженням нової інформації від інформаційних змінних „позиція” та „мобільність”. Зв’язок між вузлами „активність” та „намір ворога” (батьківський вузол) роз’єднано, в результаті чого вузол „активність” став кореневим. Оскільки всі стани вузла „активність” мають таку ж апріорну ймовірність, що і раніше, то маємо максимальну апріорну невизначеність:
![]() біт.
біт.
Рис.2 ілюструє ситуацію, коли надходить така інформація:
![]() ,
,
![]() .
.
Умовні ймовірності можна визначити з вузла „активність”, що приводить до такої умовної ентропії:
![]() =
=
![]()
![]() .
.
Таким чином, ступінь зменшення невизначеності за рахунок надходження згаданої нової інформації складає: ![]() біт.
біт.
Аналіз впливу оновлення ймовірності
Хоча зменшення невизначеності – це основна причина збору інформації, в мережі протікають інші тонкі інформаційні процеси, які відіграють вирішальну роль у процесі прийняття рішень щодо наступних дій. Якщо розподіл ймовірностей для змінної ![]() , щодо якої формулюється гіпотеза, такий, що
, щодо якої формулюється гіпотеза, такий, що ![]() для деякого
для деякого ![]() , то із значною мірою впевненості можна стверджувати, що поточна ситуація визначається значенням
, то із значною мірою впевненості можна стверджувати, що поточна ситуація визначається значенням ![]() . Однак такі випадки є досить рідкісними. Якщо змінна
. Однак такі випадки є досить рідкісними. Якщо змінна ![]() має велике число станів, то значну роль відіграє тип розподілу. Фактично форма розподілу визначає нашу довіру до ідентифікації конкретної ситуації. Крім того, в динамічній постановці задачі характер ситуації буде змінюватись у часі. Можливо, що нові спостереження ніколи не нададуть точного описання ситуації, але послідовність розподілу ймовірностей, яку ми отримуємо з надходженням нової інформації, повинна інформувати нас щодо того, як змінюється ситуація.
має велике число станів, то значну роль відіграє тип розподілу. Фактично форма розподілу визначає нашу довіру до ідентифікації конкретної ситуації. Крім того, в динамічній постановці задачі характер ситуації буде змінюватись у часі. Можливо, що нові спостереження ніколи не нададуть точного описання ситуації, але послідовність розподілу ймовірностей, яку ми отримуємо з надходженням нової інформації, повинна інформувати нас щодо того, як змінюється ситуація.
Кількісне описання ситуативних змін можна отримати таким чином. Нехай в деякий момент ![]() значення змінної
значення змінної ![]() мають розподіл
мають розподіл ![]() . В момент
. В момент ![]() надходять нові значення спостережень, які формують розподіл
надходять нові значення спостережень, які формують розподіл ![]() ; припустимо, що цієї нової інформації досить для визначення змін в поточній ситуації. Потрібно визначити – наскільки гіршою буде ефективність прийнятого рішення у випадку, якби нова інформація не надійшла? Тобто без нової інформації рішення буде грунтуватись на розподілі
; припустимо, що цієї нової інформації досить для визначення змін в поточній ситуації. Потрібно визначити – наскільки гіршою буде ефективність прийнятого рішення у випадку, якби нова інформація не надійшла? Тобто без нової інформації рішення буде грунтуватись на розподілі ![]() при фактичному розподілі
при фактичному розподілі ![]() . Оскільки фактичним розподілом
. Оскільки фактичним розподілом ![]() буде
буде ![]() , то невизначеність ситуації визначається за виразом:
, то невизначеність ситуації визначається за виразом:
![]() ,
,
що відрізняється від значення ![]() , яке є мірою невизначеності у випадку отримання нової інформації. Таким чином, збільшення невизначеності внаслідок неотримання нової інформації визначається за виразом [19, 20]:
, яке є мірою невизначеності у випадку отримання нової інформації. Таким чином, збільшення невизначеності внаслідок неотримання нової інформації визначається за виразом [19, 20]:
![]() . (7)
. (7)
Вираз (7) – це відстань Кульбака між розподілами ![]() і
і ![]() , яка є завжди додатньою. Необхідно відзначити, що ступінь невизначеності, характерний для оновленого розподілу
, яка є завжди додатньою. Необхідно відзначити, що ступінь невизначеності, характерний для оновленого розподілу ![]() , може бути більшим ніж для
, може бути більшим ніж для ![]() . Це свідчить про те, що отримання нової інформації не завжди зменшує невизначеність, але без оновлення неможливо рухатися вперед.
. Це свідчить про те, що отримання нової інформації не завжди зменшує невизначеність, але без оновлення неможливо рухатися вперед.
Аналіз ефективності приладів збору даних
Розглянемо спочатку коцепцію взаємної інформації, яка буде використана для аналізу ефективності приладів для збору даних. Взаємна інформація для двох випадкових змінних ![]() і
і ![]() визначається так [20]:
визначається так [20]:
![]() . (8)
. (8)
Можна також показати, що
![]() , (9)
, (9)
і ![]() . (10)
. (10)
Тобто взаємна інформація – це об’єм інформації, який містить змінна ![]() щодо
щодо ![]() . Іншими словами,
. Іншими словами, ![]() показує наскільки, в середньому, випадкова змінна
показує наскільки, в середньому, випадкова змінна ![]() зменшує невизначеність, що міститься в
зменшує невизначеність, що міститься в ![]() .
.
Розглянемо просту мережу, яка містить елементи, необхідні для аналізу ефективності приладів збору даних (рис. 1).
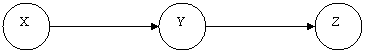
Рис. 1 Проста мережа Байєса: ![]() – змінна, щодо якої формулюється
– змінна, щодо якої формулюється
гіпотеза; ![]() – інформаційна змінна;
– інформаційна змінна; ![]() – вузол, який означає
– вузол, який означає
прилад для отримання інформації.
Гіпотеза щодо змінної ![]() оцінюється на основі інформації, що забезпечується змінною
оцінюється на основі інформації, що забезпечується змінною ![]() , а
, а ![]() отримує дані від приладу
отримує дані від приладу ![]() . Очевидно, що змінні
. Очевидно, що змінні ![]() і
і ![]() мають однакові стани, наприклад,
мають однакові стани, наприклад, ![]() може приймати значення „розташування”, а
може приймати значення „розташування”, а ![]() – прилад для визначення типу „розташування”. Якщо прилад працює надійно, то його перехід в стан
– прилад для визначення типу „розташування”. Якщо прилад працює надійно, то його перехід в стан ![]() приводить до переходу
приводить до переходу ![]() у відповідний стан
у відповідний стан ![]() з одиничною ймовірністю:
з одиничною ймовірністю:
![]() , (11)
, (11)
де ![]() і
і ![]() , тобто
, тобто  , а маржинальні ймовірності
, а маржинальні ймовірності ![]() і
і ![]() зв’язані так:
зв’язані так: ![]() . Для ідеального приладу
. Для ідеального приладу ![]() . Іншими словами, між змінні
. Іншими словами, між змінні ![]() і
і ![]() зв’язані зашумленим інформаційним каналом. Наявність шумового фактору відображається умовними ймовірностями
зв’язані зашумленим інформаційним каналом. Наявність шумового фактору відображається умовними ймовірностями ![]() . Зв’язок між
. Зв’язок між ![]() і
і ![]() , який квантується умовними ймовірностями
, який квантується умовними ймовірностями ![]() , представляє знання, які використовуються для формування висновку щодо
, представляє знання, які використовуються для формування висновку щодо ![]() .
.
При апріорних ймовірностях ![]() змінної
змінної ![]() початкова невизначеність гіпотези визначається за виразом:
початкова невизначеність гіпотези визначається за виразом: ![]() . Апостеріорна невизначеність гіпотези у випадку, якщо прилад приймає стан
. Апостеріорна невизначеність гіпотези у випадку, якщо прилад приймає стан ![]() , складає:
, складає:
![]() , (12)
, (12)
де 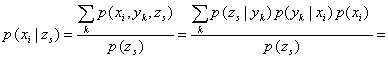
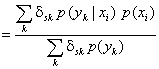 . (13)
. (13)
Оскільки для ідеального приладу ![]() , то отримаємо:
, то отримаємо:
![]() . (14)
. (14)
Таким чином, для ідеального приладу маємо:
![]()
![]() . (15)
. (15)
Використовуючи властивість незалежності вузлів МБ, можна показати, що ступінь зменшення невизначеності приладом ![]()
![]() . (16)
. (16)
Оскільки для ідеального приладу виконується рівність ![]() , то він зменшує невизначеність щодо
, то він зменшує невизначеність щодо ![]() на
на ![]() . Якщо надійність приладу менша одиниці, то його здатність зменшувати невизначеність погіршиться на величину:
. Якщо надійність приладу менша одиниці, то його здатність зменшувати невизначеність погіршиться на величину:
![]() . (17)
. (17)
Тобто менше значення ![]() свідчить про вищу ефективність приладу. В загальному випадку ефективність приладів (датчиків інформації) можна оцінити так:
свідчить про вищу ефективність приладу. В загальному випадку ефективність приладів (датчиків інформації) можна оцінити так:
– прийняти ![]() за кореневий вузол з апріорними ймовірностями
за кореневий вузол з апріорними ймовірностями ![]() ;
;
– задати ![]() – його можливі стани і обчислити
– його можливі стани і обчислити ![]() ; умовні розподіли
; умовні розподіли ![]() , обчислені для кожного значення
, обчислені для кожного значення ![]() , використати для оцінювання умовної ентропії
, використати для оцінювання умовної ентропії ![]() , а за виразом (8) обчислити
, а за виразом (8) обчислити ![]() ; аналогічно обчислити
; аналогічно обчислити ![]() .
.
Ефективність мережі Байєса
Розглянемо МБ, яка складається з ![]() вузлів (рис. 2). Кореневий вузол
вузлів (рис. 2). Кореневий вузол ![]() представляє змінну, щодо якої формулюється гіпотеза, а вузли без нащадків представляють
представляє змінну, щодо якої формулюється гіпотеза, а вузли без нащадків представляють ![]() інформаційну змінну:
інформаційну змінну: ![]() . Всі інші вузли – проміжні, вони допомагають передавати інформацію (свідчення) від інформаційних змінних до головної, для якої формулюється гіпотеза.
. Всі інші вузли – проміжні, вони допомагають передавати інформацію (свідчення) від інформаційних змінних до головної, для якої формулюється гіпотеза.
Структура мережі вважається встановленою, якщо визначено число вузлів та зв’язки між ними. Надалі необхідно визначити умовні ймовірності, які встановлюють кількісний рівень зв’язків між вузлами, тобто визначають функціональну структуру мережі. Отримання нової інформації від інформаційних змінних дає можливість оцінювати та оновлювати розподіл ймовірностей для основної змінної ![]() .
.
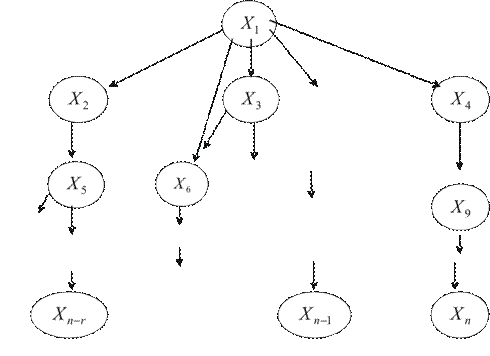
Рис. 2. Узагальнена структура МБ з однією змінною, щодо якої формулюється гіпотеза та множиною інформаційних змінних
Припустимо, що випадкова змінна ![]() приймає значення на множині
приймає значення на множині ![]() . Позначимо через
. Позначимо через ![]() , тобто додавання тут виконується по всіх значеннях
, тобто додавання тут виконується по всіх значеннях ![]() . Ефективність МБ визначається її здатністю використовувати інформацію, що надходить в процесі функціонування об’єкта, що моделюється, для оновлення розподілу основної змінної. Очевидно, що така здатність МБ визначається коректністю функціональної специфікації, яка визначає ступінь впливу інформаційних змінних на основну. Таким чином за міру ефективності можна вибрати міру цього впливу, яка може бути встанолена за допомогою взаємної інформації:
. Ефективність МБ визначається її здатністю використовувати інформацію, що надходить в процесі функціонування об’єкта, що моделюється, для оновлення розподілу основної змінної. Очевидно, що така здатність МБ визначається коректністю функціональної специфікації, яка визначає ступінь впливу інформаційних змінних на основну. Таким чином за міру ефективності можна вибрати міру цього впливу, яка може бути встанолена за допомогою взаємної інформації:
![]() . (18)
. (18)
Для конкретного значення ![]() випадкових змінних
випадкових змінних ![]() і
і ![]() взаємна інформація
взаємна інформація ![]() є увігнутою функцією від
є увігнутою функцією від ![]() . Аналогічний результат можна отримати і для МБ. Розглянемо першу складову у правій частині рівняння (18):
. Аналогічний результат можна отримати і для МБ. Розглянемо першу складову у правій частині рівняння (18):
![]() , (19)
, (19)
де ![]()
![]() ; (20)
; (20)
![]() множина батьківських вузлів для вузла
множина батьківських вузлів для вузла ![]() [21]. Вираз (20) записано із врахуванням умовної незалежності змінних, характерною для структури МБ. Оскільки умовні ймовірності
[21]. Вираз (20) записано із врахуванням умовної незалежності змінних, характерною для структури МБ. Оскільки умовні ймовірності ![]() представляють собою постійні значення, то
представляють собою постійні значення, то ![]() є лінійною функцією від
є лінійною функцією від ![]() . Таким чином, ентропія
. Таким чином, ентропія ![]() , яка є увігнутою функцією від
, яка є увігнутою функцією від ![]() , буде також увігнутою функцією від
, буде також увігнутою функцією від ![]() .
.
Для другого члена у правій частині (19) можна записати:
![]() . (21)
. (21)
З іншого боку
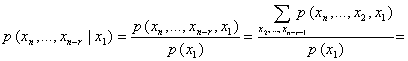
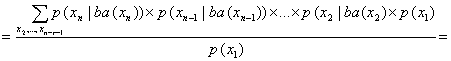
![]() . (22)
. (22)
Таким чином, після визначення умовних ймовірностей ![]() величина
величина ![]() залишається фіксованою, а ентропія
залишається фіксованою, а ентропія ![]() – лінійна функція
– лінійна функція ![]() . Оскільки
. Оскільки ![]() – це різниця між увігнутою функцією від
– це різниця між увігнутою функцією від ![]() і лінійною функцією від
і лінійною функцією від ![]() , то вона буде увігнутою функцією від
, то вона буде увігнутою функцією від ![]() .
.
Якщо змінна, щодо якої формулюється гіпотеза, може приймати ![]() альтернатив, тобто
альтернатив, тобто ![]() , то розподіл ймовірностей
, то розподіл ймовірностей ![]() визначається числами:
визначається числами: ![]() . Множина усіх таких функцій розподілу утворює симплекс вимірності
. Множина усіх таких функцій розподілу утворює симплекс вимірності ![]() в просторі
в просторі ![]() , який визначається співвідношеннями:
, який визначається співвідношеннями: ![]() та
та ![]() . А різниця
. А різниця ![]() – увігнута функція, визначена на цьому симплексі. Таким чином, існує така зв’язана підмножина
– увігнута функція, визначена на цьому симплексі. Таким чином, існує така зв’язана підмножина ![]() цього симплексу, на якій взаємна інформація є константою, що відповідає глобальному максимуму. Тобто, якщо
цього симплексу, на якій взаємна інформація є константою, що відповідає глобальному максимуму. Тобто, якщо ![]() – одна точка, то функція
– одна точка, то функція ![]() має єдиний глобальний максимум у цій точці.
має єдиний глобальний максимум у цій точці.
Апріорний розподіл ймовірностей ![]() для змінної, щодо якої формулюється гіпотеза, відображає характер поточної ситуації на будь-якому етапі прийняття рішень. Зміна ситуації приводить до зміни параметрів розподілу на розглянутому вище симплексі. Можна зробити такий висновок: якщо
для змінної, щодо якої формулюється гіпотеза, відображає характер поточної ситуації на будь-якому етапі прийняття рішень. Зміна ситуації приводить до зміни параметрів розподілу на розглянутому вище симплексі. Можна зробити такий висновок: якщо ![]() належить множині
належить множині ![]() , то функціонально визначена мережа дає можливість максимально використати всю інформацію, яка була зібрана на поточний момент. По мірі того як розподіл
, то функціонально визначена мережа дає можливість максимально використати всю інформацію, яка була зібрана на поточний момент. По мірі того як розподіл ![]() зміщується по відношенню до
зміщується по відношенню до ![]() , відображаючи тим самим еволюцію ситуації, здатність мережі Байєса використовувати нову інформацію зменшується. Для того щоб повернутись до оптимального режиму роботи необхідно змінити її функціональну специфікацію таким чином, щоб розподіл
, відображаючи тим самим еволюцію ситуації, здатність мережі Байєса використовувати нову інформацію зменшується. Для того щоб повернутись до оптимального режиму роботи необхідно змінити її функціональну специфікацію таким чином, щоб розподіл ![]() став частиною множини
став частиною множини ![]() або знаходився на її границі.
або знаходився на її границі.
Така зміна потребує виконання наступних дій (однієї або обох):
– змінити множину спостережуваних змінних таким чином, щоб зібрана інформація мала вищу ступінь наближення до явно вираженої ситуації;
– змінити положення проміжних вузлів і, тим самим, зв’язки між елементами мережі таким чином, щоб розповсюдження свідчень (інформації) по мережі краще відповідало новій поточній ситуації.
Необхідно підкреслити, що увігнутість функції ![]() – це важливий факт, який свідчить про те, що МБ є самою ефективною по відношенню до деякої унікальної ситуації або множини ситуацій, що відповідають унікальній точці або зв’язаній області ймовірнісного симплексу. Також необхідно підкреслити, що МБ часто має суб’єктивну природу, вона відображає процес прийняття рішення конкретною особою. В зв’язку з цим природно виникає запитання: чи є цей процес ефективним та внутрішньо консистентним? Чи коректно відображає створений ланцюжок причинних зв’язків дійсний перебіг ситуацій? На ці запитання можна дати стверджувальну відповідь, якщо взаємна інформація
– це важливий факт, який свідчить про те, що МБ є самою ефективною по відношенню до деякої унікальної ситуації або множини ситуацій, що відповідають унікальній точці або зв’язаній області ймовірнісного симплексу. Також необхідно підкреслити, що МБ часто має суб’єктивну природу, вона відображає процес прийняття рішення конкретною особою. В зв’язку з цим природно виникає запитання: чи є цей процес ефективним та внутрішньо консистентним? Чи коректно відображає створений ланцюжок причинних зв’язків дійсний перебіг ситуацій? На ці запитання можна дати стверджувальну відповідь, якщо взаємна інформація ![]() приймає максимальне значення в точці ймовірнісного симплексу, яка наближається до точки, що відповідає поточній ситуації. Якщо ж ці точки знаходяться далеко одна від одної, то суб’єктивний процес створення мережі був неефективним і, можливо, внутрішньо неконсистентним.
приймає максимальне значення в точці ймовірнісного симплексу, яка наближається до точки, що відповідає поточній ситуації. Якщо ж ці точки знаходяться далеко одна від одної, то суб’єктивний процес створення мережі був неефективним і, можливо, внутрішньо неконсистентним.
Висновки
Графічні моделі у вигляді мереж Байєса представляють собою зручний і важливий інструмент аналізу невизначеностей різної природи. Представлення моделі процесу у вигляді графу дає можливість швидкого осмислення ситуацій і наглядного представлення взаємодії елементів (змінних). При розробці моделі процесу виконується розв’язка якісних аспектів від кількісних. Це дає можливість спочатку зосередитись на побудові причинної структури мережі, не беручи до уваги ймовірнісні аспекти. При цьому необхідно тільки чітко розуміти причини та можливі наслідки тих чи інших дій. На другому етапі побудови МБ необхідно визначити умовні ймовірності для зв’язків. Для розв’язку цієї задачі можна скористатись статистичними даними (якщо це можливо) або суб’єктивними знаннями експертів. Очевидно, що обидва способи потребують додаткових досліджень.
The effectiveness of Bayes network functioning is considered from the point of view of uncertainties distribution across the network. A criterion for quantitative analysis is given for estimation of information volume that is distributed between the elements of a network. Also recommendations are given to construct a network structure.
1. Long W. Medical diagnosis using a probabilistic causal network // Applied Artificial Intelligence. – 1989. – № 3. – P. 367-383.
2. Charniak E. The Bayesian analysis of common sense medical diagnosis / Proceedings of the American Association Conference on Artificial Intelligence. – 1993. – P. 70-73.
3. Bioch J.C., van der Meer O., Potharst R. Classification using Bayesian neural networks / Proceedings Benelarn’95, Brussel University. – 1995. – P. 79-90.
4. Milho I., Fred A., Albano J., Baptista N., Sena P. An Auxiliary system for medical diagnosis based on Bayesian belief networks / http://www.lx.it.pt, 2000. – 6 p.
5. Korrapathi R., Mukherjee S., Chalam K.V. A Bayesian framework to determine patience compliance in glaucoma cases / http:www.adams.mgh.harvard.edu, 2004. – 1 p.
6. Kjerulff U. Constructing Bayesian Networks / Report of Reykjavik University, April, 2005. – 77 p.
7. Nelson D.J. Finding useful questions: on Bayesian diagnosticity, probability, impact, and information gain // Psychological Review, 2005. – Vol. 112, № 4. – P. 979-999.
8. Huang K., Yang H., King I., Lyu Mr. Maximizing sensitivity in medical diagnosis using biased minimax probability machine // IEEE Transaction on Biomedical Engineering, 2006. – Vol. 53, № 5. – P. 821-831.
9. Lerner U., Parr R., Koller, D., Biswas G. Bayesian fault detection and diagnosis in dynamic systems / 17 National Conference on Artificial Intelligence, 2000. – 7 p.
10. Garg S. Controls and health management technologies for intelligent aerospace propulsion systems / NASA-TM, 2004. – 212915. – 28 p.
11. Leray Ph. Apprentissage diagnostic de systemes complexes: reseaux de neurons et reseaux Bayesiaens / de Universite Paris 6, PhD Thesis, 1998. – 180 p.
12. Portinale L., Bobbio A. Beyesian networks for dependability analysis: an application to digital control reliability / 17 National Conference on Artificial Intelligence, 2000. – 10 p.
13. Cheng J., Greiner R. Learning Bayesian belief network classifiers: algorithms and system / Canadian conference on artificial intelligence (CSCSI01), 2001. – P. 141-151.
14. Stephenson T.A., Bourlard H., Bengio S., Morris A.C. Automatic speech recognition with both acoustic and articulatory variables / 6 International conference on spoken language processing, Beijing, October, 2000. – P. 951-954.
15. Rossi P.E., Allenby G.M. Bayesian statistics and marketing // Marketing Science, 2003. – Vol. 22, № 3. – P. 304-328.
16. Бідюк П.І. Оцінювання і прогнозування стану малого підприємства за допомогою мережі Байєса // Наукові праці Миколаївського державного гуманітарного університету ім. Петра Могили, 2005. – Вип. 44. – C. 7-29.
17. Niedermayer D. An Introduction to Bayesian networks and their contemporary applications / http://www.niedermayer.ca, 2006. – 13 p.
18. Robinson R.W. Counting unlabeled acyclic digraphs / Proceedings of The Fifth Australian Conference on Combinatorial Mathematics, Melbourne, Australia, 1976. – P. 28-43.
19. Терентьев А.Н., Бидюк П.И. Эвристический метод построения байесовских сетей / Міжнародна НТК „Інтелектуальні системи підтримки прийняття рішень та прикладі аспекти сучасних інформаційних технологій. – Євпаторія, травень 2006. – т. 1, C. 401-403.
20. Chow C.K., Liu C.N. Approximating discrete probability distributions with dependence trees. // IEE Transactions on information theory, May 1968. – Vol. IT-14, № 3. – 6 p.
21. Бидюк П.И., Терентьев А.Н., Гасанов А.С. Построение и методы обучения Байесовских сетей // Кибернетика и системный анализ, 2005. – 4, – C. 133 – 147.
22. Алемов С.В., Бардачев Ю.Н. Литвиненко В.И.Фефелов А.А.,Сташенко А.А., Шерстюк, В.Г. Стешенко О.А. Использование байесовских сетей для оценки санитарного состояния объектов //Моделювання та керування станом еколого-економічних систем регіону .– Випуск 3,2006 с.14.-26
23. Бидюк П.И., Литвиненко В.И. Фефелов А.А., Шерстюк В.Г., Тригуб С.Н. Алгоритмы классификации на основе байесовских сетей //Збірник наукових праць у пяти томах другої міжнародної наукової конференції Інтелектуальні системи прийняття рішень та прикладні аспекти інформаційних технологій/ Євпаторія 2006,Том 2, с.177-183.
24. Фефелов А.А., Бидюк П.И., Литвиненко В.И. Использование имунных алгоритмов для приближенного расчета маргинальных вероятностей в задаче вывода суждений из Байесовских сетей// Системні технології. Регіональний міжвузівський збірник наукових праць – Випуск 6(47). Дніпропетровськ, 2006. – с.235-244.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.