УДК 662.75

Характеристики некоторых элементов системы управления, в том числе и объекта управления, как статические, так и динамические, могут обладать нежелательными для разработчика системы управления свойствами, например, нелинейность статической характеристики, большая постоянная времени, интегрирующие свойства и пр. Нелинейность статической характеристики объекта управления - явление нежелательное, но часто встречающееся в практике. Например, морское судно, как объект управления, имеет неоднозначную статическую характеристику, что приводит в некоторых случаях к появлению автоколебаний в системе управления судном с авторулевым [1]. Нелинейности типа "люфт" имеют место в случаях, когда в системе управления есть механические передачи.

Известны методы коррекции динамических свойств элементов, путем включения корректирующего звена параллельно элементу, или в виде местной обратной связи [2]. Там же описан метод вибрационной линеаризации нелинейной статической характеристики, основанный на создании автоколебаний в части системы, включающей нелинейное звено. При этом для медленно меняющихся во времени сигналов нелинейное звено проявляет себя как линейное.

 Задача одновременного улучшения как статических свойств элемента, так и его динамических свойств является актуальной.

На рис.1 приведена структурная схема системы коррекции характеристик элемента, позволяющая в ряде случаев не только "исключить" нелинейность статической характеристики, но также изменить динамические характеристики элемента. На рис.1 приняты следующие обозначения: K_О(P) -передаточная функция элемента системы управления, характеристики которого желательно изменить; K_Ж(P) - передаточная функция желаемая; K_К(P) - передаточная функция корректирующего звена.

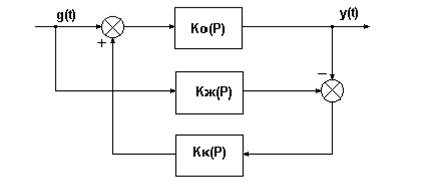
Рис.1 Структурная схема системы коррекции характеристик элемента

Передаточная функция системы коррекции, связывающая входное воздействие g(t) с выходным сигналом y(t), равна

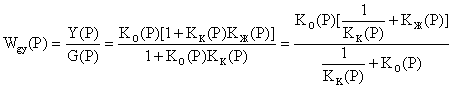 .              (1)

Из (1) видно, что если K_К(P) устремить в бесконечность, то в пределе передаточная функция всей схемы будет равна желаемой передаточной функции K_Ж(Р). Как показывают результаты моделирования, в случае, когда корректируемый элемент - звено первого порядка и не имеет запаздывания - хороший результат (приближение передаточной функции всей схемы к желаемой) получается при условии K_К(P) = K - постоянный коэффициент.

На рис.2 приведены результаты моделирования: а) статическая характеристика объекта; б) статическая характеристика того же объекта, но с коррекцией.

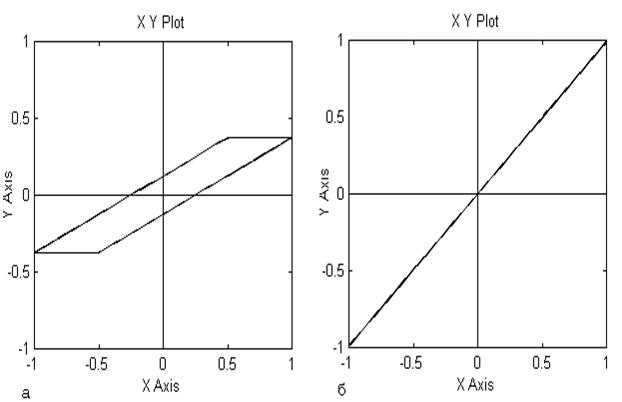
Рис.2 а) статическая характеристика элемента;

б) статическая характеристика того

же элемента, но с коррекцией при KЖ(Р) = 1, KК(P) = 100

Предлагаемая схема коррекции характеристик элементов позволяет не только исключить зону нечувствительности в статической характеристике, но также изменить динамические свойства элемента. На рис.3 приведены результаты моделирования объекта, со статической характеристикой типа "люфт" и инерционным звеном первого порядка. Как видно (рис.3,б) в системе коррекции объект практически становится пропорциональным звеном.

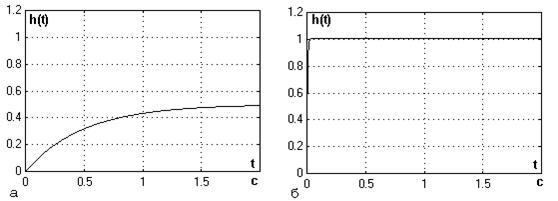
Рис. 3 а) переходная характеристика элемента;

б) переходная характеристика того же элемента

с коррекцией К_Ж(Р)=1; К_К(Р)=100

Элемент с интегрирующим свойством может быть преобразован в пропорциональное звено (рис.4) и наоборот, пропорциональное звено может быть преобразовано в интегратор (рис.5). Во всех рассмотренных случаях в качестве статической характеристики элемента принята нелинейность типа "люфт" с зоной нечувствительности 1,0.

В тех случаях когда элемент имеет порядок второй и выше, либо когда в элементе есть запаздывание, корректирующее звено следует выбирать из условия устойчивости замкнутого контура, образуемого звеньями К_О(Р) и К_К(Р).

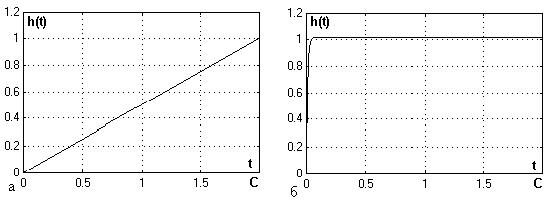
Рис. 4 а) переходная характеристика элемента;

б) переходная характеристика того же элемента

с коррекцией К_Ж(Р)=1/Р; К_К(Р)=100

На рис.6 приведен пример коррекции характеристики объекта, передаточная функция которого имеет вид:

Статическая характеристика объекта - нелинейность типа "люфт".

Передаточная функция желаемая принята следующего вида:

.

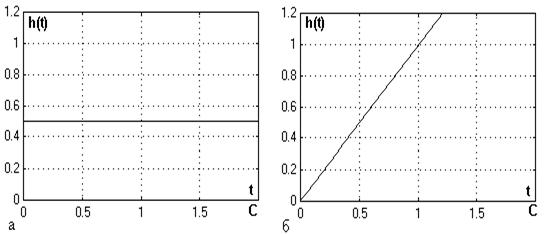
Рис. 5 а) переходная характеристика элемента;

б) переходная характеристика того же элемента,

но с коррекцией К_Ж(Р)=1/Р; К_К(Р)=100

Передаточная функция корректирующего звена определена из условия минимальной колебательности при минимальном времени переходного процесса:

 .

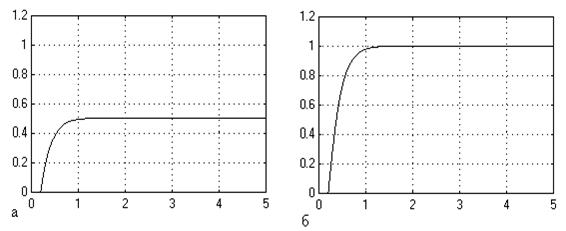
Рис. 6 а) переходная характеристика элемента;

б) переходная характеристика того же элемента с коррекцией

Во всех приведенных примерах моделирование проводилось в пакете MATLAB-Simulink.

1.                  Кринецкий И.И., Пичугин Е.Д. Исследование автоматического управления курсом судна с учетом нелинейных характеристик системы // Судовождение и связь. Труды ЦНИИ морского флота, - Л.: Транспорт, 1967, вып. 83. – С.13–16.

2.                  Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования- М.: Наука, 1972. – 768 с.