Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК  658.562

ОЦЕНКА КАЧЕСТВА  ЧИСЛОВОГО МНОГОПАРАМЕТРИЧЕСКОГО КОНТРОЛЯ

Болычевцев А.Д., Болычевцева Л.А., Быстрицкая Л.Б.

Проблема качества актуальна во все времена. Гарантом качества выпускаемой предприятием продукции был и остается производственный контроль [1]. Чтобы выполнять свою миссию гаранта, контроль сам должен быть качественным.

Еще сравнительно недавно понятие «качество контроля» не имело четкого толкования и лишь изредка проскальзывало в периодической печати как синоним  достоверности контроля. Между тем это понятие имеет самостоятельную расшифровку, опирающуюся на общую дефиницию качества любого объекта познания, независимо от его физической природы. Впервые оно определено и строго аргументировано в работе  [2]. В ней же  найдены и проанализированы показатели качества числового однопараметрического контроля. При определенных условиях они могут быть распространены и на многопараметрический контроль.

Цель данной работы – установить эти условия и конкретизировать структуру соответствующих показателей качества.

Исходные сведения. Согласно [2], качество контроля есть его свойство соответствовать своему назначению. Количественно его (качество) можно оценить показателем, именуемым потерями качества и представляющим собой математическое ожидание так называемой функции потерь  [3]. Аргументы последней суть требуемые (идеальные) и действительные (реальные) выходные параметры системы контроля

                                                .                                                        (1)

При этом под системой контроля понимается совокупность контролируемого объекта и контролирующего устройства, а под ее выходными параметрами – двоичные сигналы, отражающие результаты контроля: «да» или «нет»  («0» или «1»)

                                                                          (2)

x и x’  –  истинное и измеренное  значение контролируемого параметра объекта, N – его норма (область его допустимых значений).

 Общий принцип конструирования функции потерь – штраф за ошибку [3]. При его реализации для однопараметрического контроля каждой ошибке первого рода ставится в соответствие некоторый штраф  с1, каждой ошибке второго рода – штраф с2, отсутствие ошибки не штрафуется (штраф с0 = 0).

Специфика многопараметрического контроля. Многопараметрические объекты контроля имеют несколько контролируемых параметров, описываемых векторной величиной . Результаты их измерения представляются вектором , не совпадающим с вектором контролируемых параметров . Измерения по каждой компоненте вектора несвязанны и проводятся независимо друг от друга, так что случайные величины ,  i = 1, 2, …, n  независимы.

Норма N вектора контролируемых параметров есть  n-мерный параллелепипед с длиной сторон, равной ширине поля допуска по каждому из параметров. Попадание точки    внутрь параллелепипеда

                                                         N                                                                   (3)

равносильно положительному исходу контроля объекта, непопадание – отрицательному исходу. Иначе говоря, объект считается годным тогда и только тогда, когда результат измерения каждого контролируемого параметра попадает внутрь соответствующего интервала

                                         [ x _{н i} , x _{в i} ],        i =  1,  2, …, n,                                  (4)

x _{н i}  и  x _{в i}   –  нижняя и верхняя границы поля допуска по i-му контролируемому параметру. Если хотя бы один результат измерения    не удовлетворяет (4), исход контроля отрицателен.

Многопараметрический контроль обычно строится по такой схеме.

В той или иной заранее установленной последовательности проверяются контролируемые параметры объекта на их соответствие допуску (4).

Как только для какого-то, например  k-го  (k < = n) контролируемого параметра,  условие (4) не выполняется

                                                                   [ x _{н i} , x _{в i} ],                                                     (5)

цепочка их проверок прерывается, исход контроля считается отрицательным и объект бракуется.

-        Если по результатам проверок все контролируемых параметров оказались в допуске, исход контроля считается положительным, а объект годным, т.е. принимается к использованию по назначению.

              Изложенное показывает, что идеальный    r   и реальный   r^/    исходы многопараметрического контроля предстают в форме конъюнкции (произведения) соответствующих идеальных   r_i   и реальных   r^/_i   исходов однопараметрического контроля (контроля по каждому контролируемому параметру):

                                          r =  ,        r^/  =  ,                                          (6)

где

                                 =            =                    (7)

             Из-за несовершенства методики контроля и неточности используемых технических средств его исходы  могут оказаться ошибочными  (r  r/ ):  годный объект бракуется и, наоборот, негодный объект принимается за качественный. Это так называемые ошибки первого и второго рода. Их вероятности участвуют в формировании качества исхода контроля.

 Качество положительного исхода. При многопараметрическом контроле наибольший интерес представляет оценка качества контроля принятого к использованию объекта. Очевидно, в этом случае исход контроля полагается положительным

                                                               r/  =  1                                                            (8)

и, как следствие, k =  n.

При составлении функции потерь возможны разные подходы, соответствующие разным влияниям ошибок контроля на экономические последствия функционирования проконтролированного объекта.  Выделим два из них.

Первый подход исходит из того, что любая ошибка второго рода  одинаково нежелательна. В этом случае каждой ошибке естественно приписывать одинаковый штраф с. Функция потерь приобретает вид двоичной случайной величины

                                       l(r)  =                                                     (9)

В символической записи функции потерь аргумент  r/ опущен, поскольку он принимает постоянное значение  r/ = 1.

Второй подход исходит из того, что разные контролируемые параметры  xi  имеют разный вес в формировании качества объекта. В этом случае ошибкам контроля будем приписывать разные штрафы  ci. Функцию потерь представим в виде

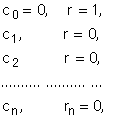                          =                             (10)

тем самым расшифровав, какой именно контролируемый параметр стал первопричиной ошибки контроля объекта в целом.

В записи (10) событие  r = 1  означает, что положительный исход контроля (8) верен. Вероятность этого события характеризует степень доверия к исходу, т.е. его достоверность

                                              p₀  =   P { r = 1 }.                                                      (11)

Каждое из событий  ri = 0 представляет собой ошибку второго рода по i-му параметру. Именно ей мы и приписываем штраф ci Ее вероятность есть апостериорно-условный риск заказчика [4]

                                                      .                                               (12)       

Покажем, что для реальных условий контроля  запись (10) можно рассматривать как некую дискретную  случайную величину С, принимающую значения с0, с1, с2, …, сn  с соответствующими вероятностями p0, p21, p22,…,p2i . Действительно.

Достоверность p0 контроля объекта в целом равна произведению достоверностей p0i исходов контроля по каждой компоненте (контролируемому параметру) xi,, i = 1,…n.

                                    p₀  =  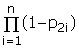=                                                   (13)

Раскроем последнее произведение

p₀  =  1 – + 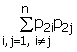–  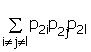+ ….+ (-1)ⁿ .          (14)

При правильной организации многопараметрического контроля вероятности p_2i, i = 1, 2,…, n малы (в противном случае контроль был бы неэффективен). Поэтому определяющий вклад в достоверность   p₀   вносят первые два члена записи (14), так что

                                            p₀  1 – .                                                            (15)

Отсюда следует

                              p₀  +  p₂₁  +  p₂₂  + ….+  p_2n      1.                                             (16)

 Составим  таблицу из двух строк и  n + 1 столбца

                                    c0       c1        c2    …..     cn

p0      p21        p22            p2n                                                      (17)

Учитывая приближение (16), ее можно рассматривать как ряд распределения дискретной случайной величины  С,  принимающей значения с0, с1, с2,…сn  c  вероятностями   p0,  p21,  p22,….,  p2n.

Теперь нетрудно найти потери качества контроля как математическое ожидание функции потерь l (r) (дискретной случайной величины  С ), определяемой ее первой (9) и второй (10) структурами. Для первой структуры

                                            =  M l (r) = c p2  ,                                                   (18)

где p2  – апостериорно-условный риск заказчика при многопараметрическом контроле, любые ошибки второго рода которого одинаково нежелательны. Пропорциональная зависимость от p2  показывает, что в этом случае сам риск  p2 может выступать в роли потерь качества контроля. Для второй структуры 

                                           = M l (r) = = ,                                   (19)

где  –  символ скалярного произведения двух векторов

                              = (c1, c2, …., cn),       = (p21,  p22,…., p2n).                           (20)

    Итак, потери качества многопараметрического контроля при его положительном исходе равны скалярному произведению вектора штрафов на вектор апостериорно-условных рисков заказчика. В частном случае, когда влияние ошибок контроля на экономические последствия функционирования объекта одинаковы  (ci = c,   i = 1, 2,…, n),

                                                           =  c .                                                    (21)

Из сравнения (21) и (18) следует, что сумма апостериорно-условных рисков заказчика выступает в качестве апостериорно-условного риска контроля в целом

                                                              p2 = .                                                      (22)

Качество отрицательного исхода. Как следует из сказанного выше, объект бракуется при первом же отрицательном исходе проверок  контролируемых параметров (5). Это значит, что он возвращается поставщику, который его (объект) после его дополнительных проверок либо ликвидирует (отправит на свалку, демонтирует на запчасти и т.п.), либо восстанавливает (ремонтирует), либо вновь передает заказчику как ошибочно забракованный. Издержки на дополнительные проверки в двух первых случаях – по вине самого изготовителя, в последнем – по вине заказчика. Они и определяют цену ошибки (а следовательно, и штраф за ошибку) первого рода.

Размер штрафа, очевидно, зависит от той информации, которой сопровождается возвращение изготовителю забракованного объекта. Возможны два варианта такого возвращения: а) с указанием контролируемого параметра, ставшего причиной отрицательного исхода контроля; б) без какой-либо информации.

При первом варианте автоматически оказываются известными и все предшествующие контролируемые параметры, подвергшиеся проверке и подтвердившие свою «благонадежность» (соответствие допуску). Этот вариант связан с большими, чем второй вариант, издержками контроля. Поэтому он практикуется реже. Тем более, что, независимо от того, указан «виновник» брака или нет, поставщику все равно придется проверять все контролируемые параметры заново. Ведь часть параметров оказывается непроверенной вообще, а в проверенную часть параметров могли вкрасться ошибки.

Из сказанного следует, что, независимо от того, какой контролируемый параметр явился причиной забракования объекта, в качестве штрафа за ошибку первого рода следует взять стоимость дополнительных проверок всей совокупности контролируемых параметров. Именно эта стоимость и служит ценой ошибки контроля.

В некоторых случаях может оказаться, что дополнительные проверки стоят дороже, чем сам объект контроля. В этом случае его проще изъять (демонтировать), не подвергая проверкам. Тогда роль штрафа за ошибку первого рода возьмет на себя стоимость объекта.

Таким образом, при отрицательном исходе контроля, т.е. при выполнении

                                                           r = 0                                                                      (23)

функция потерь l(r) имеет такой же вид, как и при положительном исходе контроля в случае одинаковой нежелательности любой ошибки

                                                  l(r) = 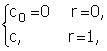                                                   (24)

и, значит, потери качества контроля опишутся аналогичной (18) зависимостью

                                                  =  M l (r) = c p1,                                                   (25)

в которой p1 –  риск изготовителя при многопараметрическом контроле. Он определяется соотношением, аналогичным  риску заказчика (22)

                                                          p1 = ,                                                       (26)

p1i – вероятность ошибки первого рода по  i-му контролируемому параметру.

Полученные результаты раскрывают структуру показателей качества многопараметрического контроля, позволяя продвинуться в решении задачи его анализа.

1.      Болычевцев А.Д. Контроль как гарантия качества продукции и требования к точности  его измерительных средств // Метрология. – 2000. - № 11. – С. 20-32.

2.      Болычевцев А.Д., Цапенко М.П., Шенброт И.М. Качество контроля // Измерительная техника. – 1984. - № 11. – С. 3-5.

3.      Основы автоматического управления / Под редакцией В.С. Пугачева. – М.: Наука, 1968. –  680 с.    

4.      Пономаренко М.Ф. Методы достоверности контроля. – К.: КПИ, 1983. –162 с.