УДК 681.518.5:677.017.4:677.053.756
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ВЛИЯНИЯ ТЕХНОЛОГИИ ШЛИХТОВАНИЯ НА ИЗМЕНЕНИЕ ЖЕСТКОСТИ ТЕКСТИЛЬНЫХ НИТЕЙ
Боярчук В.П., Сыс В.Б.
Актуальность. Анализ исследований. Одним из главных способов повышения качества ошлихтованной основы в технологическом процессе шлихтования (ТПШ) является применение систем оперативного контроля величины жесткости текстильных нитей (ВЖТН), как основного параметра механических свойств ТН (МСТН) [1,2]. Известно [3-4], что такая система позволит повысить качество проведения, оперативность и точность управления ТПШ.
Разработка данных систем требует не только теоретического анализа, но и экспериментального исследования с целью уточнения воздействий технологии шлихтования на изменение жесткости ТН и возможностей их физического взаимодействия. Тем более слабо исследованы вопросы измерения жесткости ошлихтованных основ и влияния основных технологических параметров (натяжение, вытяжка, величина приклея и влажность основ и т.д.), как главных показателей качества шлихтования, на изменение жесткости.
Следует отметить большую сложность в организации экспериментальных исследований изменения МСТН в ходе шлихтования, что связано с требованиями, предъявляемыми к измерительной аппаратуре и условиям проведения эксперимента. Так же необходимо учитывать, что попытки измерения жесткости с помощью существующих контактных средств контроля жесткости из-за наличия существенных недостатков [3-5] не нашли широкого применения. Устранение всех этих недостатков позволило разработать лабораторный стенд [1,4], позволяющий не только автоматизировать процесс измерения МСТН, но и главное оперативно, с достаточной достоверностью и точностью произвести экспериментальные исследования МСТН, в том числе и ВЖТН при статических и динамических нагружениях. Принцип действия стенда позволяет имитировать устройство контроля жесткости [1,4,5].
Цель работы. Провести экспериментальные исследования по изучению влияния нелинейных свойств ТН, составляющих деформаций, вида нагружения и основных технологических параметров (натяжения, удлинения, влажности, величины приклея) шлихтования на процесс и характер изменения ее жесткости. Исследовать возможность измерения жесткости, предпосылки создания оперативного измерителя жесткости ТН и возможность организации автоматического управления технологией шлихтования по параметру жесткости основы.
Основная часть. В основу экспериментального исследования упругих свойств ТН (коэффициента жесткости ТН) на рабочих интервалах изменения деформаций были положены методы измерения жесткости:
1) по линейному приращению нагрузки – статическая жесткость на растяжение через приращение ![]() :
:
![]() ;
;
2) по коэффициенту пропорциональности (наклона) кривых растяжения – угловая ![]() и дифференциальная
и дифференциальная ![]() жесткости на растяжение:
жесткости на растяжение:
![]() ;
;
3) по линейному отклонению при полной нагрузки – статическая жесткость на растяжение полная ![]() :
:
![]() ;
;
4) линейному периодическому приращению нагрузки – динамическая жесткость на растяжение ![]() :
:
![]() ;
;
где ![]() ;
; ![]() ,
, ![]() – максимальное натяжение и относительное удлинение пряжи;
– максимальное натяжение и относительное удлинение пряжи; ![]() ,
, ![]() – предварительное натяжение и относительное удлинение (деформация) пряжи;
– предварительное натяжение и относительное удлинение (деформация) пряжи; ![]() – площадь поперечного сечения TH;
– площадь поперечного сечения TH; ![]() – модуль упругости;
– модуль упругости; ![]() – удлинение контролируемого участка ТН;
– удлинение контролируемого участка ТН; ![]() – длина образца ТН;
– длина образца ТН; ![]() – угол наклона линейной зависимости кривой растяжения к оси
– угол наклона линейной зависимости кривой растяжения к оси ![]() ;
; ![]() ,
, ![]() , (
, (![]() ,
, ![]() ) – приращения (дифференциал) натяжения и удлинения в точке кривой растяжения ТН;
) – приращения (дифференциал) натяжения и удлинения в точке кривой растяжения ТН; ![]() ,
, ![]() – приращение натяжения и относительного удлинения пряжи при дополнительной деформации;
– приращение натяжения и относительного удлинения пряжи при дополнительной деформации; ![]() ,
, ![]() (
(![]() ,
, ![]() ) – приращение (амплитудные значения) натяжения и относительной деформации ТН при периодическом нагружении.
) – приращение (амплитудные значения) натяжения и относительной деформации ТН при периодическом нагружении.
Для реализации поставленных целей следует признать целесообразным поэтапное проведение экспериментальных исследований над ТН на разработанном экспериментальном стенде [1,4] при статических и динамических нагружениях:
1) снятие кривых растяжения и исследование возникновения остаточных деформаций;
2) исследование влияний натяжения ТН на изменение жесткости;
3) исследование влияний влажности на изменение жесткости;
4) исследование влияний величины приклея на изменение жесткости;
5) исследование влияния динамического нагружения на изменение МСТН.
В качестве образцов исследования в основном выступала мягкая и ошлихтованная хлопчатобумажная пряжа 29 текс №34,5. Выбор величины нагрузки, длительности действия нагрузки приближался к реальным условиям обработки ТН при шлихтовании.
При статическом нагружении на ТН прикладывалось импульсное воздействие, при динамическом – гармоническое, регистрировалось удлинение образца и натяжение, после чего воздействие снималось и снова регистрировались показания. Затем изменяли амплитуду воздействия и снова повторяли измерения.
С целью повышения точности измерений и осуществления испытаний при упругих удлинениях образца базовой длиной была выбрана длина ![]() =500 мм, импульсы деформации задавались малой амплитуды (2.5,5,7.5,10,12.5,15,17.5,20,22.5,25 мм), а натяжение измерялось относительно своего максимального значения 350 гс и приводилось к относительным единицам.
=500 мм, импульсы деформации задавались малой амплитуды (2.5,5,7.5,10,12.5,15,17.5,20,22.5,25 мм), а натяжение измерялось относительно своего максимального значения 350 гс и приводилось к относительным единицам.
Для усреднения полученных характеристик эксперимент проводился по 5 раз на нескольких образцах ТН одной линейной плотности.
Основные статистические показатели экспериментов, аппроксимация и проверка адекватностей регрессионных зависимостей экспериментальным данным проводилась с помощью программ MathCAD по стандартным методикам [5,6]. При экспериментальном исследовании влияния основных технологических параметров остальные поддерживались в постоянных пределах. Коэффициент жесткости определялся по вышеприведенным методам 1-4. Затем полученные коэффициенты сопоставлялись между собой.
1. Снятие кривых растяжения и исследование возникновения остаточных деформаций.
По методике эксперимента ТН фиксированной длины ![]() подвергали растяжению. При этом последовательно и плавно увеличивали удлинение тем самым и нагрузку, фиксировали значение деформации ТН до и после снятия нагрузки, контролировали восстановление (релаксацию) начальных размеров ТН. В ходе экспериментов исследовалась степень проявления упругих свойств ТН, т.е. при каких нагрузках ТН будет сохранять упругие свойства, а при каких появляется остаточное значение деформации, дающее необратимое увеличение длины ТН и ухудшение механических свойств.
подвергали растяжению. При этом последовательно и плавно увеличивали удлинение тем самым и нагрузку, фиксировали значение деформации ТН до и после снятия нагрузки, контролировали восстановление (релаксацию) начальных размеров ТН. В ходе экспериментов исследовалась степень проявления упругих свойств ТН, т.е. при каких нагрузках ТН будет сохранять упругие свойства, а при каких появляется остаточное значение деформации, дающее необратимое увеличение длины ТН и ухудшение механических свойств.
|
|
|
|
а) |
б) |
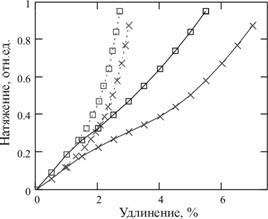
Рис. 1 График кривых растяжения мягкой (![]() ,
,![]() ) и ошлихтованной (
) и ошлихтованной (![]() ,
,![]() ) ТН:
) ТН:
а) с отображением общей (сплошная) и упругой (пунктирная) составляющих деформации
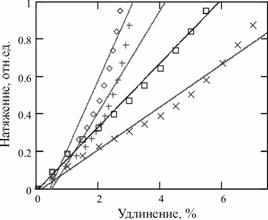
б) с аппроксимацией кривых растяжений линейными зависимостями
|
|
|
|
а) |
б) |
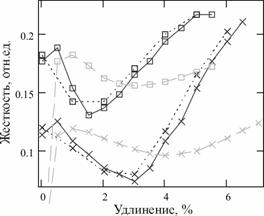
Рис. 2 Графики изменения жесткости мягкой (![]() ) и ошлихтованной (
) и ошлихтованной (![]() ) ТН по кривым
) ТН по кривым
растяжения при общей (а) и упругой (б) составляющих деформации, найденные разными методами: 1 – сплошная, 2 – пунктир, 3 – штриховая
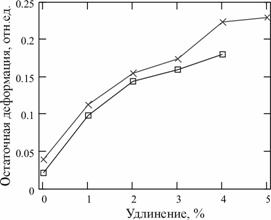
Рассчитывалось процентное отношение величины упругой и остаточной составляющих деформации закрепленной ТН относительно базовой длины ![]() . По полученным данным построены типичные графики зависимости кривых растяжений для мягкой (МО) и ошлихтованной основы (ШО) (рис. 1-а) и проведена их аппроксимация линейными зависимостями (рис. 1-б)
. По полученным данным построены типичные графики зависимости кривых растяжений для мягкой (МО) и ошлихтованной основы (ШО) (рис. 1-а) и проведена их аппроксимация линейными зависимостями (рис. 1-б)
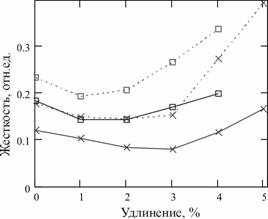
Аппроксимация кривых растяжения линейными зависимостями и обработка экспериментальных данных позволила определить коэффициенты жесткости на всем и отдельных интервалах исследований и построить графики их изменения от деформации (рис. 2).
Результаты проведенных экспериментальных исследований по кривым растяжения позволяют сделать следующие выводы:
1) Деформация хлопчатобумажной ТН состоит из нескольких составляющих: упругой (упругая и ускоренно-эластическая) и остаточной (медленно-эластической и пластической). Характер и величина деформации ТН зависят от характера и величины приложенного усилия, и длительности действия нагрузки.
2) С увеличением нагрузки доля обратимой (упругой) части деформации в общей деформации значительно уменьшается, а необратимая составляющая деформации ТН имеет накопительный характер.
3) Допустимые значения деформации при протяжке ТН в шлихтовании должны ограничиваться упругой составляющей и ускоренно-эластической деформацией, которая быстро исчезает после снятия нагрузки.
4) Несмотря на то, что статическая характеристика кривых растяжения ТН в общем случае нелинейна, она хорошо аппроксимируются линейными зависимостями, а при малых значениях относительной деформации обладает строго линейной зависимостью.
5) Для увеличения точности процесс измерения жесткости необходимо реализовать в пределах упругой составляющей деформации. На процесс изменения жесткости ТН значительное влияние оказывает долевое соотношение составляющих деформации ТН.
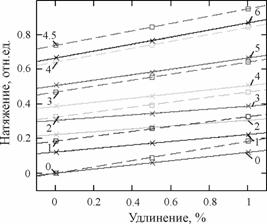
2. Экспериментальное исследование влияний натяжения ТН на изменение жесткости.
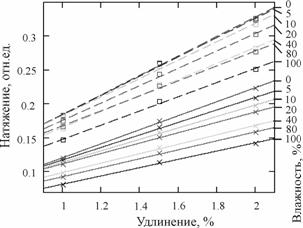
В данном случае проводились независимые эксперименты, при которых на ТН прикладывали дополнительное предварительное натяжение P=(0;0.117;0.216;0.307;0.395;0.502;0.673) – для мягкой, P=(0;0.173;0.319;0.47;0.643;0.737) –для ошлихтованной, которые соответствуют деформациям ![]() =(0;1;2;3;4;5;6;). Затем ТН подвергали дополнительному фиксированному удлинению
=(0;1;2;3;4;5;6;). Затем ТН подвергали дополнительному фиксированному удлинению ![]() =0.5, 1% (2.5, 5 мм). В ходе таких экспериментов постоянно определяли натяжение.
=0.5, 1% (2.5, 5 мм). В ходе таких экспериментов постоянно определяли натяжение.
На основании экспериментальных исследований построены графики растяжения ТН при дополнительном удлинении от приложенной нагрузки (рис. 3-а, рис. 3-б).
Результаты проведенных экспериментальных исследований влияния натяжения ТН на изменение жесткости позволяют сделать следующие выводы:
1) При малых значениях относительной деформации математическая модель ТН адекватна линейной модели, главным показателем которой является жесткость ТН, как показатель истинно упругой деформации материала, исключающего влияние эластического и пластического компонентов деформации.
2) Деформация ТН приводит сначала к снижению потом к возрастанию натяжения, а следовательно, и жесткости и сильнее сказывается для ошлихтованной основы и одновременно вызывает резкое увеличение постоянной составляющей.
3) Вычисление жесткости по методам 1-3 дают схожие результаты, а отличия методов измерения жесткости связаны с влиянием составляющих деформаций на процесс измерения жесткости, которая определяется: в методе 1 – упругой составляющей деформации по концам интервала измерения; в методе 2 – упругой составляющей деформации всего интервала измерения, поэтому значения жесткости получаются усредненными для всего рассматриваемого интервала изменения упругой деформации; в методе 3 – полной деформации, содержащее упругие и остаточные (эластические и пластические) составляющие деформации.
Влияние остаточных деформаций на процесс измерения жесткости приводит к тому, что метод 3 не позволяет оценивать коэффициент жесткости по упругой составляющей деформации и может точно оценивается по методам 1,2. Поэтому вычисления жесткости по методам 1, 2 дают наиболее схожие результаты, и их можно рекомендовать для реализации в процессе измерения ВЖТН, как основного показателя упругой деформации. Если же определять жесткость ТН применительно к упругой составляющей деформации, то результаты методов 1-3 будут одинаковые.
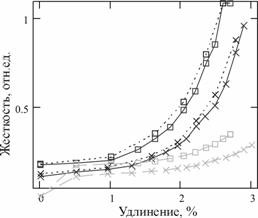
4) Схожесть графиков изменения жесткости от прикладываемого натяжения рис. 3-б подтверждает правильность эксперимента.
|
|
|
|
а) |
б) |
Рис. 3 Исследования влияния натяжения на изменение жесткости мягкой (![]() )
)
и ошлихтованной (![]() ) ТН: а) определение жесткости по линейным зависимостям
) ТН: а) определение жесткости по линейным зависимостям
от предварительной деформации,(0-6)% при разных натяжениях;
б) графики изменения жесткости от удлинения при разных натяжениях ТН,
найденные методами: 1 – сплошная, 2 – пунктир, 3 – штриховая.
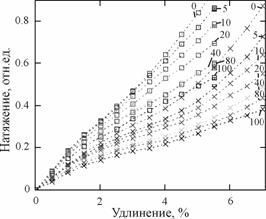
3. Экспериментальное исследование влияния влажности основы на жесткость.
В данном случае производились независимые эксперименты над ТН с разной относительной влажностью (0, 5,10, 20,40, 80, 100). ТН нагружали предварительной нагрузкой, создающее удлинение ![]() =1%, затем ТН растягивали на
=1%, затем ТН растягивали на ![]() =0.5, 1% и определяли натяжение. Изменения влажности во время проведения опытов не превышали ±5 процентов, и были вызваны изменением параметров окружающей среды и естественным испарением. Длительность эксперимента не превышала 1 мин.
=0.5, 1% и определяли натяжение. Изменения влажности во время проведения опытов не превышали ±5 процентов, и были вызваны изменением параметров окружающей среды и естественным испарением. Длительность эксперимента не превышала 1 мин.
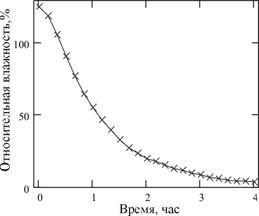
Для получения относительной влажности образец ТН смачивался дистиллированной водой до полного впитывания и отжимался на отградуированной плюсовке. Влажность контролировалась методом взвешивания и составляла в начале эксперимента 110% -115%, а в конце эксперимента 5% -15%. В ходе эксперимента влажность образца уменьшалась за счет естественного испарения влаги. Измерения проводились через каждые 15 минут на новых образцах основы.
Так как скорость испарения влаги зависит от многих параметров [6], то для определения влажности была построена зависимость влажности исследуемого образца от времени сушки (рис. 4).
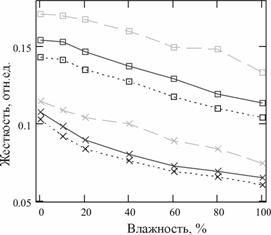
График кривых растяжения при изменении влажности приведен на рис. 5, а при дополнительном удлинении ![]() =0.5, 1% и предварительной деформации
=0.5, 1% и предварительной деформации ![]() =1% – на рис. 6-а Обработка экспериментальных данных позволила определить коэффициенты жесткости ТН и построить график изменения жесткости от влажности рис. 6-б.
=1% – на рис. 6-а Обработка экспериментальных данных позволила определить коэффициенты жесткости ТН и построить график изменения жесткости от влажности рис. 6-б.
Результаты проведенных экспериментальных исследований влияния влажности основы на жесткость позволяют сделать следующие выводы:
1) Максимум ошлихтованной основы согласно характеристике рис. 6-б наблюдается в пределах влажности 0% - 20%, которые можно рекомендовать для технологии проведения шлихтования.
2) С увеличением влажности общая деформация ТН увеличивается, но уменьшается доля упругой составляющей, что приводит к уменьшению значений жесткости мягкой и ошлихтованной основ, причем для ошлихтованной основы такое изменение наиболее существенное.
3) Характеристика влияния влажности на жесткость ТН в общем виде нелинейна и наиболее существенна для ошлихтованной основы, чем для мягкой, но при малых изменениях параметров ее можно линеаризовать, т.е. она может быть заменена линейной.
4) Увеличение жесткости при уменьшении влажности объясняется тем, что идет закрепление структуры волокон ТН, коэффициент трения между волокнами увеличивается, что приводит к увеличению нагрузки при постоянном удлинении ТН. Такое увеличение наиболее чувствительно для ошлихтованной основы.
|
|
|
|
Рис. 4 Зависимость изменения влажности основы от времени сушки |
Рис. 5 Кривые растяжения при изменении влажности,% мягкой ( |
|
|
|
|
а) |
б) |
Рис. 6 Исследование влияния влажности основы на жесткость мягкой (![]() )
)
и ошлихтованной (![]() ) ТН: а) определение жесткости по линейным зависимостям
) ТН: а) определение жесткости по линейным зависимостям
при разной влажности; б) зависимости изменения жесткости от влажности, найденные
разными методами: 1 – сплошная, 2 – пунктир, 3 – штриховая
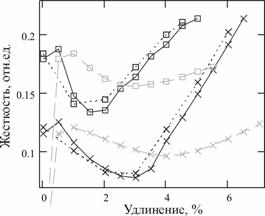
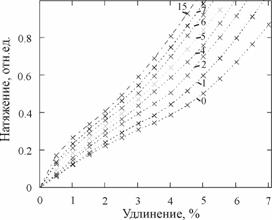
4. Исследование влияний величины приклея на изменение жесткости.
Производились независимые эксперименты с ТН, при которых ТН с разной величиной приклея 0,1,2,4,6,8,10,12 нагружалась предварительной нагрузкой, создающее предварительное растяжение ![]() =1%. Затем ТН подвергалась растяжению на
=1%. Затем ТН подвергалась растяжению на ![]() =0.5, 1% и фиксировалось значение натяжения при растяжении ТН.
=0.5, 1% и фиксировалось значение натяжения при растяжении ТН.
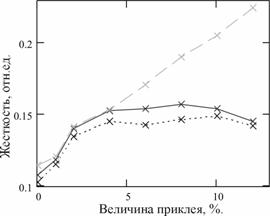
Обработка экспериментальных данных позволила построить графики кривых растяжения (рис. 7а) и изменения жесткости от величины приклея (рис. 7-б).
|
|
|
|
а) |
б) |
Рис. 7 Исследование влияния величины приклея на изменение жесткости ТН:
а) кривые растяжения при изменении величины приклея,%;
б) графики изменения жесткости от величины приклея, найденные
разными методами: 1 – сплошная , 2 – пунктир, 3 – штриховая
Результаты проведенных экспериментальных исследований влияния величины приклея на изменение жесткости позволяют сделать следующие выводы:
1) Наибольшая чувствительность величины жесткости основы согласно характеристике рис. 7б наблюдается при величинах приклея в пределах от 4% - 10%, которые можно рекомендовать для технологии проведения шлихтования.
2) Величина приклея существенно влияет на изменение жесткости ТН, при этом, характеристика в общем виде нелинейна, но при малых изменениях параметров ее можно заменить линейной.
3) С увеличением приклея общая деформация ТН уменьшается, но увеличивается доля упругой составляющей и жесткость. Такое увеличение жесткости объясняется тем, что идет склеивание структуры волокон ТН, коэффициент трения между волокнами увеличивается, что приводит к увеличению нагрузки при постоянном удлинении ТН.
4) При увеличении величины приклея жесткость ТН постепенно уменьшается, это объясняется тем, что дополнительный приклей, скапливаясь на поверхности ТН, ослабляет склеивание волокон. При этом ТН теряет эластичность и становится хрупкой
5. Исследование влияния динамического нагружения на изменения МСТН.
В данном случае на ТН прикладывали периодическое импульсное воздействие ![]() =1% и регистрировали удлинение и натяжение образца ТН до тех пор, пока их значения не установятся постоянными. Затем изменяли предварительное натяжение ТН, составляющее для мягкой основы
=1% и регистрировали удлинение и натяжение образца ТН до тех пор, пока их значения не установятся постоянными. Затем изменяли предварительное натяжение ТН, составляющее для мягкой основы ![]() =(0;0.12;0.223;0.306;0.386;0.503), для ошлихтованной основы
=(0;0.12;0.223;0.306;0.386;0.503), для ошлихтованной основы ![]() =(0;0.183;0.326;0.469;0.64), соответствующих предварительной деформации
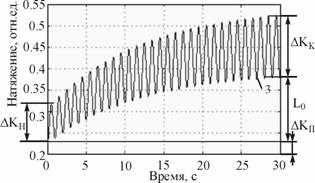
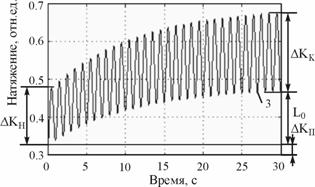
=(0;0.183;0.326;0.469;0.64), соответствующих предварительной деформации ![]() =(0;1;2;3;4;5;), и снова повторяли измерения. В ходе каждого эксперимента получали осциллограммы, рис. 7, где
=(0;1;2;3;4;5;), и снова повторяли измерения. В ходе каждого эксперимента получали осциллограммы, рис. 7, где ![]() – величина предварительного статического натяжения нити;
– величина предварительного статического натяжения нити; ![]() и
и ![]() — величина натяжения, возникающих в нити соответственно при первом (начальное натяжение) и предпоследнем (конечное натяжение) циклах нагружения;
— величина натяжения, возникающих в нити соответственно при первом (начальное натяжение) и предпоследнем (конечное натяжение) циклах нагружения; ![]() =30 – количество циклов;
=30 – количество циклов; ![]() – величина остаточных деформаций нити.
– величина остаточных деформаций нити.
По измерениям отдельных участков осциллограмм кривых натяжения ТН (рис. 8) определялись основные показатели растяжения ТН при динамическом нагружении (табл. 1): ![]() ,
, ![]() – жесткость пряжи на растяжение в первом (начальная) и предпоследнем (конечная) циклах, как отношение отклонений возникающих усилий и деформации пряжи по методу 4;
– жесткость пряжи на растяжение в первом (начальная) и предпоследнем (конечная) циклах, как отношение отклонений возникающих усилий и деформации пряжи по методу 4; ![]() ,
, ![]() ,
, ![]() ,
, ![]() – начальные и конечные значения натяжения пряжи и их приращения;
– начальные и конечные значения натяжения пряжи и их приращения; ![]() – остаточная деформация.
– остаточная деформация.
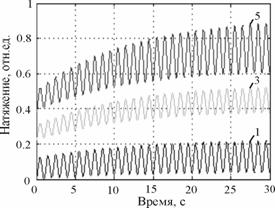
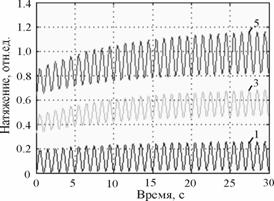
Рис. 8. Осциллограммы изменения кривых натяжения мягкой (![]() ) и ошлихтованной (
) и ошлихтованной (![]() ) ТН при переменной нагрузки по опытам (1,3,5) с определением основных показателей растяжения
) ТН при переменной нагрузки по опытам (1,3,5) с определением основных показателей растяжения
Таблица 1
Исследование влияния динамического нагружения на изменения МСТН
|
мягкая основа |
||||||||||
|
№ |
|
|
|
|
|
|
|
|
|
|
|
1) |
0 |
0.12 |
0.039 |
0.217 |
0.1780 |
0.0390 |
0.1200 |
0.1780 |
0.1200 |
0.1780 |
|
2) |
0.12 |
0.223 |
0.232 |
0.381 |
0.2690 |
0.1120 |
0.1030 |
0.1490 |
0.1030 |
0.1490 |
|
3) |
0.223 |
0.306 |
0.378 |
0.523 |
0.3680 |
0.1550 |
0.0830 |
0.1450 |
0.0830 |
0.1450 |
|
4) |
0.306 |
0.386 |
0.48 |
0.633 |
0.4590 |
0.1740 |
0.0800 |
0.1530 |
0.0800 |
0.1530 |
|
5) |
0.386 |
0.503 |
0.609 |
0.884 |
0.6610 |
0.2230 |
0.1170 |
0.2750 |
0.1170 |
0.2750 |
|
6) |
0.503 |
0.669 |
0.732 |
1.125 |
0.8960 |
0.2290 |
0.1660 |
0.3930 |
0.1660 |
0.3930 |
|
ошлихтованная основа |
||||||||||
|
№ |
|
|
|
|
|
|
|
|
|
|
|
1) |
0 |
0.183 |
0.021 |
0.254 |
0.2330 |
0.0210 |
0.1830 |
0.2330 |
0.1830 |
0.2330 |
|
2) |
0.183 |
0.326 |
0.281 |
0.475 |
0.3770 |
0.0980 |
0.1430 |
0.1940 |
0.1430 |
0.1940 |
|
3) |
0.326 |
0.469 |
0.47 |
0.677 |
0.5330 |
0.1440 |
0.1430 |
0.2070 |
0.1430 |
0.2070 |
|
4) |
0.469 |
0.64 |
0.628 |
0.895 |
0.7360 |
0.1590 |
0.1710 |
0.2670 |
0.1710 |
0.2670 |
|
5) |
0.64 |
0.84 |
0.82 |
1.158 |
0.9780 |
0.1800 |
0.2000 |
0.3380 |
0.2000 |
0.3380 |
Термины конечное натяжение, удлинение и жесткость приняты условно как характеристики основной пряжи во второй фазе изменения ее структуры от многократных деформаций растяжения, то есть когда структура пряжи в первом приближении уже стабилизировалась (в нашем случае для хлопчатобумажной пряжи примерно после 30-50 циклов). Затем полученные коэффициенты сопоставлялись между собой, что позволило построить их графики (рис. 9).
|
|
|
|
а) |
б) |
Рис. 9. Исследование основных показателей мягкой (![]() ) и ошлихтованной (
) и ошлихтованной (![]() ) ТН
) ТН
от предварительного удлинения при переменной нагрузки: а) остаточной деформации ТН;
б) изменения жесткости ТН (![]() - сплошная,
- сплошная, ![]() - пунктирная)
- пунктирная)
Проведенные экспериментальные исследования по исследованию влияния динамического нагружения на изменения МСТН позволяет сделать следующие выводы:
1) При динамическом нагружении стационарной ТН наблюдается изменение натяжения и развитие остаточных деформаций в ТН.
2) На процесс измерения жесткости влияет величина и время нагружения. Жесткость ТН при циклическом нагружении увеличивается и со временем принимает установившееся значение. С увеличением нагружения ТН жесткость ТН увеличивается.
3) Ошлихтованная основа в отличии от мягкой при постоянной деформации характеризуется большими значениями натяжения (начальными, конечными значениями их приращениями), начальной и конечной жесткости, но меньшими значениями разброса жесткости и остаточного удлинения.
Выводы. На основании всех проведенных экспериментальных исследований можно сделать следующие выводы:
1. Кривая растяжения ТН, как основная ее механическая характеристика, в рабочем диапазоне значений упругой составляющих деформаций с высокой достоверностью аппроксимируется линейной зависимостью, главным показателем которой является жесткость ТН. Жесткость ТН достаточно точно определяет МСТН, долевое соотношение составляющих деформации ТН, длительность и величину нагружения и отдыха, но также и влияние технологии шлихтования (влажности, приклея и т.д.). Поэтому изменение жесткости ТН в ходе шлихтования может характеризовать процесс его проведения.
2. Исследования мягкой и ошлихтованной пряжи на экспериментальном стенде в статических и динамических режимах, основы подтверждают, что процесс шлихтования увеличивает жесткость пряжи на растяжение и снижает обрывность в ткачестве. При этом выявлено, что при определенной жесткости эта обрывность будет минимальной.
3. Значения коэффициентов жесткости закрепленной ТН, найденные в результате экспериментальных исследований с постоянной малой величиной амплитуды и временем воздействия на ТН по методам 1-4, дают схожие результаты. Это особенно заметно для методов: аппроксимации и приращения, как способов позволяющих оценивать жесткость ТН по упругой составляющей деформации. Значения результатов исследований являются того же порядка и полностью отражают динамику их измерения, что указывает на достоверность и адекватность вычислений. Разброс этих значений связан, прежде всего, с точностью измерений, нестабильностью свойств ТН и влиянием технологии шлихтования. Значения жесткости были получены в относительных единицах. Для перехода к абсолютным их значениям необходимо учитывать поправочные коэффициенты пересчета.
4. Текущее значение жесткости ТН при протяжке можно достоверно оценивать с необходимой точностью, удовлетворяющей требованиям автоматической системы управления шлихтовальной машины, по методу приращений на интервале малых упругих деформаций в области низких частот нагружений (до 20 Гц), что позволяет использовать этот метод в средствах оперативного контроля ВЖТН в процессе шлихтования.
5. Установлены зависимости между изменениями ВЖТН от предварительной нагрузки и влиянием технологии шлихтования. Хотя в общем виде эти зависимости нелинейны, но при малых отклонениях параметров в области упругих деформаций они могут быть линеаризованы. Ошлихтованная основа в отличие от мягкой характеризуется более стабильными механическими характеристиками и значениями ВЖТН.
6. Полученные результаты экспериментальных исследований показали, что каждый из основных технологических параметров шлихтования (натяжения, влажности, величины приклея) влияет на жесткость ошлихтованной основы (ШО) и на процесс ее измерения. Одним из способов получения после шлихтования адекватных статических механических характеристик ТН, а, следовательно, и поддержания жесткости ТН на постоянном уровне является удерживание основных технологических параметров в заданных пределах, устанавливаемые технологией шлихтования. Такой процесс управления как раз и реализуется в существующем ТПШ. Все это указывает о возможности стабилизации заданных значений ВЖШО с помощью основных технологических параметров шлихтования и необходимости организации управления ТПШ, обеспечивающего стабилизацию значений ВЖТН после шлихтования.
7. Существенное влияние возмущений со стороны структуры, механических характеристик ТН, технологии обработки (влажность, величина приклея и т.д.) на результаты измерения требует более тщательных исследований влияния этих внешних факторов на ВЖТН, уточняющих полученные зависимости их влияния.
Experimental researches are conducted on the experimental setting at a static and dynamic loading on the study of sizing technology influence (tension, humidity, paste value) on the change of rigidity value of fixed textile threads. The results of researches to confirm possibility to correct the value of warp rigidity to desirable value by the sizing technological parameters, to shown authenticity and adequacy of methods of rigidity measuring, possibility to measure rigidity, with necessary accuracy, satisfying the requirements of automatic control system of sizing machines, possibility to use them in controls of warp rigidity value in sizing.
1. Боярчук В.П. Исследование автоматизации технологического процесса шлихтования по изменению физико-механических свойств текстильных нитей // Міжнародна конф. “Автоматика-2007”. Збірник тез доповідей. – Ч. 1. – Севастополь: СНУЯЄтаП, –2007. С. 119–121.
2. Боярчук В.П. Математическая модель изменения физико-механических свойств текстильных нитей на участках обработки шлихтования основ// Вестник ХНТУ. –2007. –№ 3 (29). –С.116–123.
3. Боярчук В.П. Расчет и распределение оптимальных значений технологических параметров шлихтования с целью повышения качества ошлихтованной основы и снижения материальных затрат // Вестник ХНТУ. –2007. –№ 3 (29). –С.108–115.
4. Боярчук В.П. Анализ и синтез автоматической системы измерения динамических и механических свойств текстильных нитей по основным критериям качества // Вестник ХНТУ. −2006. −№1(24). −С. 124-131.
5. Кукин Г.Н. и др. Текстильное материаловедение (волокна и нити). – М.: Легпромбытиздат, 1989. – 352 с.
6. Хофманн Д. Техника измерений и обеспечение качества: Справочная книга. – М.: Энергоатомиздат, 1983. – 472 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.