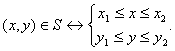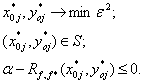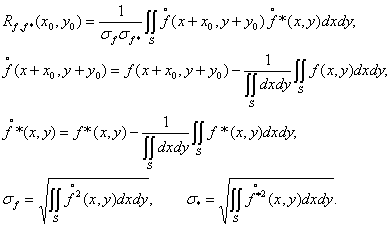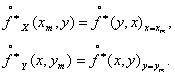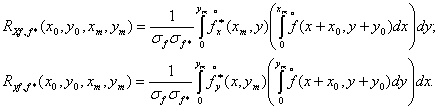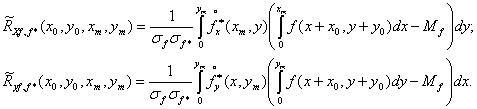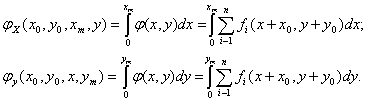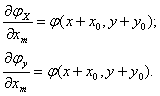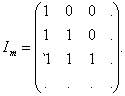Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК  534.442:534.78

ИСПОЛЬЗОВАНИЕ  ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ АВТОМАТИЗАЦИИ ОБНАРУЖЕНИЯ ОБЪЕКТОВ

Бражник Д.А.

Введение. Использование интеллектуальных систем управления, как в технологических процессах, так и в других областях деятельности на сегодняшний день является доминирующей тенденцией. При решении задач  управления на основе анализа информации от телевизионных датчиков, в условиях неопределенности, возникает задача автоматического обнаружения объектов. Одной из сторон данной задачи является анализ сцены, основанный на выделении объектов по изображению. Успешность решения данной задачи во многом определяет эффективность всего алгоритма управления системой.

Современный уровень.  Среди множества методов фрагментации изображения, прежде всего, следует выделить методы, основанные на предварительном преобразовании изображения. Среди данных методов Фурье преобразования, преобразование Адамара, Хаара, преобразование Карунена-Лоэва [1], обеспечивающие возможность выделения признаков объектов в сложном изображении, однако данные преобразования требуют значительных ресурсов и также как корреляционные методы [2] чувствительны к свойствам объектов сцены. Существенно более простыми являются проективные преобразования [3], обеспечивающие простоту алгоритма, но склонные к потере информации об объектах сцены. Существенное место среди методов анализа сцены занимают методы, основанные на выделении границ объектов [4] данный подход основан на анализе верхней части спектра и естественно требует дополнительно фильтрации изображения [5].  Таким образом, можно утверждать, что как ретроспектива, так и современные подходы не обеспечивают простоты и универсальности, что обосновывает необходимость дальнейшего анализа данного вопроса.

Цель исследования. Целью данной работы является исследование методов использования проективных преобразований для получения простой процедуры формирования опорной матрицы при дефрагментации изображения сцены.

Теоретическая часть.

                Рассмотрим сложное плоское изображение образованное сценой Ω при отсутствии пересечений изображений. В этом случае можно считать, что порожденное изображением, параметрическое поле φ=φ(x,y) определяется суммой функций, определяющих распределение параметра изображений отдельных объектов f_i(x, y).

Естественно поле изображения ограничено и, как правило, для современных технических средств это прямоугольная область S. В этом случае допустимыми являются точки

Рассмотрим задачу обнаружения заданного эталоном f* изображения. Решение данной задачи сводится к определению координат x₀, y₀ связанных либо с центром области, либо с координатами характерной точки изображения. Предположим существование процедуры ξ обеспечивающей решение данной задачи. Таким образом, для изображения  f_i(x, y) и его эталона  f *(x, y) предполагаем неопределенность координат изображения x₀, y_0, следовательно,  изображение отдельного объекта описывается с точностью до его положения в поле кадра   f_i= f_i(x+ x₀ , y+ y₀ ).   Ищем процедуру определения координат объекта заданного эталоном

Естественно меру отклонения определить как квадратичную, тогда получаем функцию цели процедуры в виде ε²= x₀²+ y₀².  С другой стороны следует учитывать, что для сложного изображения существует ограничение правильного выбора функции изображения соответствующей заданному эталону       

Данное ограничение требует введения меры близости выбранной и эталонной функций. Наиболее просто использовать корреляционную меру, для чего введем нормированную корреляционную функцию R_f,f*( x₀ , y₀), что позволит записать ограничение для заданного уровня корреляции в виде R_f,f*( x₀ , y₀)≥α .

                В таком случае на каждом шаге процедуры ξ решается задача

                Таким образом, каждый шаг процедуры является решением задачи Лагранжа и при заданном риске второе ограничение переходит в равенство. Ограничение принадлежности точки к области проверяется, как правило, аппаратурно и может не рассматриваться.  Следовательно, каждый шаг процедуры порождает функцию Лагранжа

                Причем существенным моментом является структура множителя Лагранжа λ в данной задаче. Действительно λ определяет чувствительность функции цели к ограничениям и при наличии в сцене искомого объекта λ≠0 

при этом выбранная процедура  должна базироваться на преобразовании A{φ, f*} обеспечивающем чувствительность для любых точек в S

                Для определения искомого преобразования А{φ, f*}  рассмотрим входящую в ограничения взаимнокорреляционную функцию R_f,f*.  Учитывая ограниченность области S, имеем оценку

Рассмотрим сечения эталона, что всегда можно выполнить поскольку координаты эталона известны точно

Предположим, что область интегрирования опирается на начало координат x₁=y₁=0, x₂=x_m, y₂=y_m  и подставив (10) в (9) представим корреляции с сечениями эталона R_{x f,f*}  и R_{x f,f*} в виде

Собственно в (10) внутренние интегралы определяют проективное преобразование функций изображения  на направления осей координат, а полученные оценки корреляций связаны с операцией поиска функции в аддитивной смеси. Огрубив оценку среднего функций изображения постоянным значением M_f, что естественно при усреднении по кадру получаем

Рассмотрим особенности проективных преобразований определяемых внутренним интегралом в (12) для сложного изображения j(x, y).  В этом случае  проекции изображения на направления осей X,Y определяются соотношениями

Преобразование (13) обратимо и обратным преобразованием для него является операция дифференцирования по верхнему пределу

Существенно, что поскольку эталон не зависит от сдвигов изображения данное преобразование  обеспечивает ненулевую чувствительность выбранной функции цели к положению искомого изображения в кадре для любых точек в квадрате x_m,y_m содержащем данную функцию. Таким образом, искомое преобразование А{φ, f*} определяется корреляциями между сечениями эталона и проективным преобразованием (13), а собственно искомая процедура ξ сводится к корреляционному анализу  сечений эталона и проекций изображения.

                Учитывая, что в большинстве случаев, исходное изображение описывается матрицей получение матрицы проекций F легко выполняется при помощи пары преобразований умножения на проектирующую матрицу I_m имеющую следующую легко программно генерируемую структуру. Пусть матрица изображения С квадратная, тогда проекции на вертикаль выполняются умножением на нижнюю треугольную матрицу I_m  соответствующей размерности

                        Тогда  используя единичный вектор i_m матрица проекций может быть получена очень просто F_Y=CI_m – i_m^TCi_m/m²   и   F_x=(C^T I_m)^T – i_m^TCi_m/m²   .

Исходя из удобства определения управления при движении в кадре к искомому объекту, квадратную матрицу изображения на четыре подматрицы – левую полуматрицу С₁₁,  верхнюю полуматрицу С₁₂, правую полуматрицу С₂₁ и нижнюю полуматрицу  С₂₂ размером m ^X  m/2 и соответственно сформируем треугольные подматрицы проекций F_y11, F_x12, F_y21,  F_x22  таким образом, чтобы полная матрица проекций F_xy  формировалась как сумма подматриц  проекций  F_xy= F_y11+ F_x12+ F_y21+ F_x22 .

Таким образом, использование проективной процедуры обеспечивает простой алгоритм преобразования и позволяет надеяться на  легкость анализа структуры кадра изображения сцены  после формирования матрицы проекций.

Экспериментальная часть.

                Для  проверки теоретических предположений выполнено моделирование в среде MATLAB формирования матрицы проекций и процедуры выделения объекта в сцене.

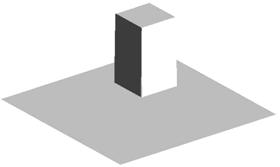
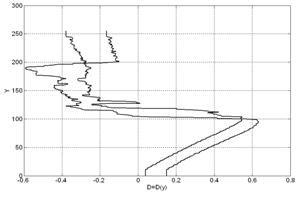
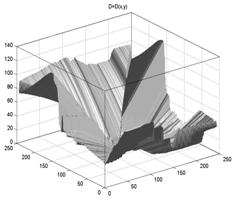
                На рисунке 1а приведено параметрическое поле простейшего изображения  и на рисунке 1б приведена его матрица двусторонних проекций.

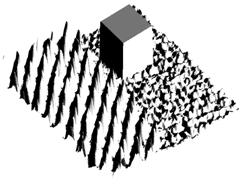
                Естественно в простейшем случае определение позиции объекта в поле кадра не представляет сложности. Однако естественно для сложных изображений поле проекций усложняется. Так на рисунке 2а приведено изображение на фоне периодической структуры с близкими амплитудами. Однако благодаря сохранению проекции вес сигнала объекта сохраняется на границах кадра, рисунок 2б.

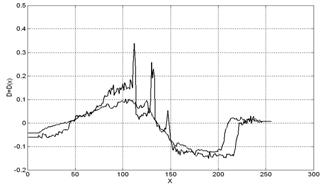
Естественно реальные сцены обладают более сложной структурой, тем не менее, информативность матрицы проекций сохраняется и в этом случае. Так для сцены приведенной на рисунке 3в по матрице проекций, рисунок 3г, легко выделить область объекта, рисунок 3д. Так для выделения наиболее крупного объекта в сцене достаточно простой процедуры анализа границ проекций рисунки 3а, 3б выделяя область максимальной корреляции с отрицательным сигналом.  На рисунке 3 приведена иллюстрация процесса выделения фрагментов сцены по анализу периферии матрицы проекций.

                Собственно приведен пример простой фрагментации на области. Процедура основана на выделении фрагментов относительно среднего значения крайних строк матрицы проекций по строкам и столбцам.

Реализация процедуры не требует длинных операций, что обеспечивает высокую скорость ее выполнения. 

Однако существует неявное, но важное обстоятельство – как видно из рисунка 3 движение от любого локального экстремума на функциях сечения матрицы проекций к центру изображения вдоль направления проекции приводит к объекту, вызывающему этот экстремум и чем существеннее экстремум, тем существеннее объект.  Таким образом, можно сделать следующие выводы.

Выводы:

1.                   Использование проективного преобразования сохраняет информацию о исходном изображении.

2.                   Построение матрицы проекций однократная процедура не требующая длинных операций.

3.                   Для изображений сложных сцен анализ матрицы проекций позволяет выделить предметные области без использования длинных операций.

4.                   Рассмотренный метод фрагментации изображения сцены  работоспособен для сложных изображений.

5.                   При решении задачи позиционирования изображения  нет необходимости пересчета матрицы проекций.

6.                   Рассмотренная методика позволяет при анализе сцены оперировать не со всей матрицей изображения, а только с четырьмя строками и столбцами матрицы.

7.                   Движение от экстремума сечения приводит к объекту, что особенно важно при необходимости быстрого фрагментирования сцены.

1.                   Прэтт У. Цифровая обработка изображений: Пер. с англ. – М.: Мир, 1982. – Кн.1 –312с., ил.

2.                   Дж.Ту, Р.Гонсалис. Принципы распознавания образов. Пер. с англ. Б.Гуревича, под ред. Ю.И.Журавлева – М., :Мир,1978,с. 407.

3.                   Хорн Б.К.П. Зрение роботов: Пер. с англ. –М.: Мир. 1989.-487с.,-ил.

4.                   Некорректные задачи в предварительной обработке визуальной информации. М. Бертеро; Т.А. Поджо. ТИИЭР: т. 76, N^о 8, 1988, стр 17-39.

5.                   Контурна сегментація зображеь з використанням вейвлет-аналізу. М.В. Полякова, В.В. Любченко / Сьома всеукраиньска міжнародна коференція «Обробка сигналів і зображень та ропізнавання образів” . Київ 2004р. Ст. 193-198.