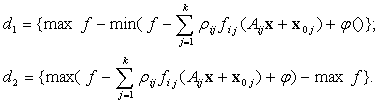УДК 534.442:534.78

Введение. Задача оптимального совмещения изображений возникает при решении задач управления летательными аппаратами [1], транспортными средствами [2], робототехническими комплексами [3] и в других задачах, где заранее известны эталонные изображения объектов, которые могут встретиться в сцене. На сегодняшний день общепринято считать наилучшим критерием качества совмещения изображений объекта и эталона взаимную корреляцию между эталоном и объектом. В практических приложениях, где существенно быстродействие, обычно используется более простая оценка – свертка [4]. Такой подход прост, но весьма требователен к вычислительным ресурсам, что исключает возможность использования простых и недорогих вычислительных систем.

Корреляционный критерий дает хорошее качество оценки, однако он также обладает рядом недостатков – главный из которых – высокие требования к эталонному изображению, т.е. требования равенства масштаба и отсутствия сдвига эталонного изображения и необходимость предварительной нормализации исходного изображения [6].

Однако для нечеткой модели, при использовании корреляции, нет возможности определить качество совмещения, так как невозможно определить причину возникновения ошибки – нарушение условий предъявления или неточность эталонного изображения.

Задача исследования – изучение возможности построения простого критерия совмещения модели и объекта, позволяющего оценить локальные отклонения модели от объекта с невысокими вычислительными затратами.

В рамках метода компенсации информационных потоков [5] для двойственной задачи предполагается использование именно корреляционной меры близости,

где w - множество точек изображения, w*(u) – множество точек эталона, u – управление.

Однако возможно и использование любой другой оценки близости, если ее сходимость обеспечивает сходимость корреляции.

Математический аппарат. Так как компенсация предусматривает генерацию эталонного изображения, рассмотрим генерируемую модель изображения w*_i  описываемую функцией f_i. Причем реально приемник за счет внешних возмущений получает смещенное и деформированное изображение

Здесь r - весовой коэффициент, А – матрица преобразования и х – вектор координат, х₀ – смещение.

В общем случае сложная модель представляется суммой элементов изображения

Для реальных условий естественно предположить, что модель не полная – то есть существует некая функция ошибки j, такая, что

Естественно, ошибка возникает или из-за возмущений объекта, или из-за грубости модели.

Корреляционный критерий, при всей своей универсальности, достаточно громоздок в вычислительном плане и не дает возможности определить природу ошибки, особенно если ошибка модели не коррелированна с объектом.

Поэтому в работе использован более простой, но более удобный и функциональный критерий

Здесь, во-первых, сохраняются координаты функции ошибки и, во-вторых, критерий разбивается на два

При этом d₁ – ошибка, связанная с неполной компенсацией, а d₂ – ошибка, связанная с неточностью модели. Понятно, что возможность использования данного критерия зависит от характера целевой функции. Естественно, что генерируемая в процессе минимизации невязки последовательность управлений тем короче, чем точнее модель соответствует объекту.

Результаты моделирования. Не останавливаясь на алгоритме фрагментации, описание которого можно найти в [5], рассмотрим три фрагмента одной сцены, приведенной на рисунке 1а. Рассматривая модель фрагментов 1 и 2 как нечеткие множества, используем функцию принадлежности, приведенную на рисунке 1б.

Так как фрагментация уже выполнена, то неопределенность, связанная с координатами объектов сцены уже снята. Однако, даже для плоского изображения, остаются неопределенными еще четыре элемента матрицы А, весовой коэффициент и собственно вид эталона – выбор гипотезы. Таким образом, необходимо минимизировать критерий по шести переменным.

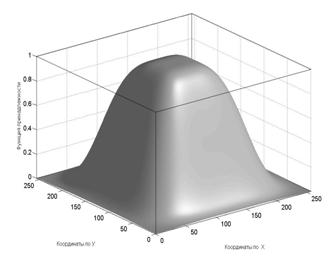
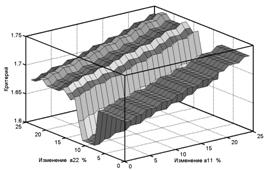
Рассмотрим изображение функции цели для первого фрагмента (рис. 2):

Изрезанность поверхности функции цели вызвана малым разрешением и дискретностью исходного изображения. Как видно из рисунка 2, поверхность функции цели имеет достаточно простую структуру и оптимизация совмещения может поддерживаться простыми процедурами.

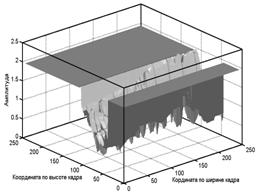
Для большего по размерам фрагмента 2 (рис. 1а) поля освещенности до компенсации и после компенсации, при требовании нулевой ошибки модели, приведены на рисунке 3а, б.

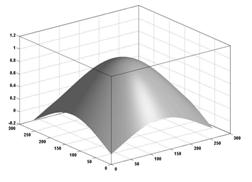
Полученная в данном случае функция цели, (рисунок 4), значительно меньше подвержена колебательности и также имеет простую структуру.

Гораздо более сложным является случай компенсации для третьего фрагмента.

В качестве модели в данном случае используем скелетный граф модели объекта со связанной с элементами графа функцией принадлежности (рис. 5а, б). Как видно из рисунка, эталонное изображение представляет собой скелетный граф, на ветви которого «натянута» функция принадлежности, представляющая собой пятно со спадающей к краям яркостью, что приводит к весьма размытому изображению.

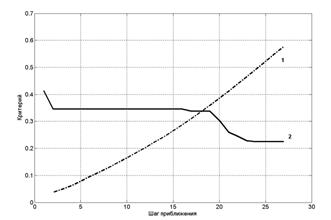
Процедура совмещения эталона и объекта на изображении в данном случае выполнялась от минимального размера модели на поле фрагмента до возникновения существенной ошибки модели. Как показали эксперименты, корреляционный критерий (график 1 на рис. 6) показывает на очень хорошее совпадение модели и объекта, а критерий максимальных отклонений (график 2 на рис. 6) дает гораздо более осторожную оценку. Т.е., можно сказать, что корреляционный критерий является гораздо более «оптимистичным».

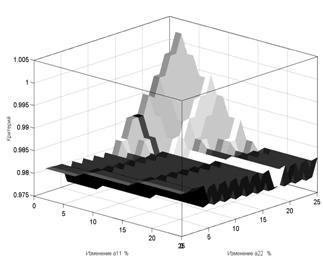
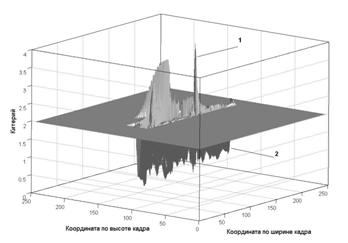
Собственно, ответ на вопрос о различном поведении критериев можно получить, анализируя полученную после компенсации поверхность, рисунок 7.

Здесь 1 – ошибка модели и 2 – остаточная некомпенсация.

Но, несмотря на малую чувствительность, результат компенсации поля изображения объекта и моделью, создаваемой генератором эталонов, вполне удовлетворительный, см. рисунок 8.

Таким образом, после выполнения операций совмещения, система формирует модель всей сцены, рисунки 9а – модель и 9б – исходная сцена.

В таблице 1 приведены значения изменения корреляции и изменения критерия максимального отклонения для двух фрагментов сцены. При этом значения критериев для различных фрагментов сцены

Таблица 1.

Значения критериев для различных фрагментов сцены.

Следовательно, в данной задаче возможно использовать критерий, по своим экстремальным свойствам эквивалентный корреляции. Однако корреляционный критерий не позволяет определить тип ошибки – т.е. мы можем выделить область с расхождениями модели и объекта, но определить природу этих расхождений мы не можем. Поэтому, с целью определения типа ошибки, мы рассматриваем критерий максимального отклонения (6), более критичный к ошибке – на рисунке 7 сразу видны точки некомпенсированные полностью, точки с частичной компенсацией (2) и перекомпенсированные (т.е. модель имеет в этой точке простой максимум) точки (1).

Выводы:

1.                   Для задачи совмещения изображений объекта в сцене и эталонного изображения может быть использован критерий максимального отклонения, дающий хорошие результаты при достаточно высокой скорости сходимости алгоритма.

2.                   Критерий максимального отклонения по своим свойствам близок к корреляции, однако требует меньших вычислительных затрат, что позволяет удешевить систему распознавания в целом.

3.                   Показано, что критерий максимального отклонения не только позволяет выделить область с ошибкой, но и позволяет определить природу расхождения – связана ли ошибка с объектом или с эталонным изображением.

1.               Рапаков Г.В. Использование средств системы MATLAB в исследованиях по безопасности полетов. Труды Всероссийской научной конференции «Проектирование инженерных и научных приложений в среде MATLAB». М.: ИПУ РАН. 2002. 842 с.: ил.

2.               Geometric modeling and computer vision/P.J. Besl. Proc. Of the IEEE, 1988, vol. N8, p. 934-958.

3.               St. Gh. Pentiuc, Radu Vatavu. Image Processing and Recognition System for a Robot Arm Control. Праці восьмої всеукраїнської міжнародної конференції „Оброблення сигналів і зображень та розпізнавання образів” 28 – 31 серпня 2006р., Київ, Україна. с.167.

4.               Хорн К.Б.П. Зрение роботов: Пер. с англ. – М.: Мир, 1989. – 487 с., ил.

5.               Бражник Д.А., Фанина Л.А. Использование проективного преобразования при фрагментации изображений сцены. Матеріали науково-практичної конференції „Інтелектуальні системи прийняття рішень та прикладні аспекти інформаційних технологій ISDMIT-2006” 15-18 травня 2006р., м. Євпаторія, Україна: Євпаторія, 2006. Том 1, - с.49