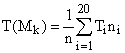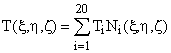УДК 515.2
АЛЬТЕРНАТИВНІ МОДЕЛІ
СТАЦІОНАРНОЇ ТЕМПЕРАТУРИ В КУБІ
Цибуленко О.В., Манойленко О.С.
Метод Монте-Карло знайшов вдале застосування до широкого кола задач [1,2]. Так як головною ідеєю методу скінчених елементів є розбиття суцільного середовища на підобласті (СЕ) і вважається, що уся головна інформація сконцентрована у вузлах СЕ, то дослідження СЕ можна виділити в окрему задачу. Зокрема, увагу авторів привертає гранична задача відновлення функції всередині СЕ, наприклад, побудова стаціонарного температурного поля на скінченому елементі. Розв’язок відшукується усередненням граничних значень, а коефіцієнти такого усереднення за допомогою методу Монте-Карло. Класична схема цього методу вимагає постановки відповідного числа експериментів (випадкових іспитів), що реалізуються за допомогою організації випадкових блукань по СЕ. В [3, 4] розглянута та обґрунтована можливість замість багатокрокових зигзагоподібних блукань з апостеріорними перехідними ймовірностями використовувати однокрокові блукання з апріорними перехідними ймовірностями і прямолінійними маршрутами.
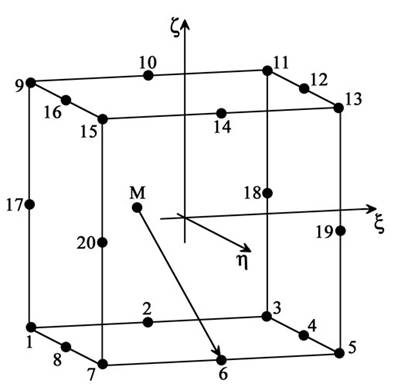 |
Рис.1 Тривимірний скінчений елемент із випадковим маршрутом
Сформулюємо задачу. Побудувати температурне поле всередині куба з 20-ма вузлами, якщо в цих вузлах температура відома (рис.1).
Метою даної роботи є порівняння альтернативних моделей побудови температурного поля всередині куба.
Статистичний експеримент полягає у спостереженні за блукаючою частинкою і фіксації факту її прибуття у вузол і (![]() ). Для маршрутизації блукань частинки зручно скористатися решіткою з комірками у формі кубів. За результатами n випробувань обчислюються відносні частоти поглинань частинок вузлом і.
). Для маршрутизації блукань частинки зручно скористатися решіткою з комірками у формі кубів. За результатами n випробувань обчислюються відносні частоти поглинань частинок вузлом і.
Температура у внутрішньому вузлі М кубу знаходиться за формулою:
|
|
(1) |
де n - загальна кількість частинок, випущених з внутрішнього вузла Мk;
Ті – температура у граничному вузлі і;
nі – кількість частинок, що фінішували у вузлі і.
Спрощена схема випадкових блукань припускає заміну апостеріорних перехідних ймовірностей апріорними. Правила випадкових блукань тепер формулюються так: блукаюча частинка стартує із довільної точки М і з ймовірністю Ni переходить у вузол і (![]() ), де Ni – базисні функції скінченого елементу. Один з 20-ти маршрутів показаний на рис. 1.
), де Ni – базисні функції скінченого елементу. Один з 20-ти маршрутів показаний на рис. 1.
Тепер температура у будь-якій точці всередині скінченого елементу визначається як математичне сподівання вузлових значень температур у граничних вузлах:
|
|
(2) |
де Ті – температура у вузлі і;
Ni – базисні функції.
Базисні функції для кубу з 20-ма вузлами мають наступний вигляд [5]:
|
|
|
|
Якщо в останній формулі переставити ![]() і
і ![]() , отримаємо
, отримаємо ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Якщо переставити
. Якщо переставити ![]() і
і ![]() , отримаємо
, отримаємо ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Розглянемо задачу на прикладі кубу з центром ваги в початку координат, де ![]() . Задамо температуру у граничних вузлах:
. Задамо температуру у граничних вузлах:
|
|
|
|
|
|
Таблиця 1.
Перехідні ймовірності для точки (0;0;0)
|
№ вузла |
Апостеріорні перехідні імовірності |
Апріорні перехідні імовірності |
№ вузла |
Апостеріорні перехідні імовірності |
Апріорні перехідні імовірності |
|
1 |
0,0426 |
-0,25 |
11 |
0,0422 |
-0,25 |
|
2 |
0,0556 |
0,25 |
12 |
0,0547 |
0,25 |
|
3 |
0,0421 |
-0,25 |
13 |
0,0422 |
-0,25 |
|
4 |
0,0550 |
0,25 |
14 |
0,0539 |
0,25 |
|
5 |
0,0427 |
-0,25 |
15 |
0,0432 |
-0,25 |
|
6 |
0,0548 |
0,25 |
16 |
0,0537 |
0,25 |
|
7 |
0,0436 |
-0,25 |
17 |
0,0549 |
0,25 |
|
8 |
0,0557 |
0,25 |
18 |
0,0547 |
0,25 |
|
9 |
0,0417 |
-0,25 |
19 |
0,0565 |
0,25 |
|
10 |
0,0552 |
0,25 |
20 |
0,0551 |
0,25 |
Таблиця 2.
Значення температури ![]() в контрольних точках кубу
в контрольних точках кубу
|
Координати точки |
За методом сіток |
За формулою (1) |
За формулою (2) |
|
(-0,5;-0,5;-0,5) |
16,35 |
16,29 |
16,24 |
|
(0;0;0) |
25,39 |
25,04 |
25,00 |
|
(0,5;0;0) |
25,44 |
25,03 |
25,00 |
Перевірити істинність отриманих перехідних ймовірностей можна за допомогою стержневої аналогії. Для цього розглянемо 20-вузловий куб як конструкцію з 12 прямолінійних стержнів, на кожний з яких припадає по три вузла. Розподіл маси в такому трьох вузловому найпростішому дискретному елементі підпорядковується правилу Сімпсона, тобто в центральний вузол треба помістити маси в 4 рази більше ніж в кожний з периферійних. Але периферійні вузли лежать на стику трьох ребер куба. Таким чином у вершині куба маса в 3/4 рази відрізняється від маси зосередженої на середині ребер.
Отже апостеріорні перехідні ймовірності відповідають фізичному змісту. Що неможливо сказати про апріорні перехідні ймовірності, які мають від’ємні значення. Отже закон великих чисел у формі Я. Бернуллі ![]() , на якому ґрунтувалась заміна апостеріорних перехідних ймовірностей базисними функціями, і який давав добру збіжність для елементів низьких порядків [3,4], не підтверджується для кубу з 20-ма вузлами. Такі аномалії (від’ємні перехідні ймовірності) зустрічаються в елементах вищих порядків [5,6].
, на якому ґрунтувалась заміна апостеріорних перехідних ймовірностей базисними функціями, і який давав добру збіжність для елементів низьких порядків [3,4], не підтверджується для кубу з 20-ма вузлами. Такі аномалії (від’ємні перехідні ймовірності) зустрічаються в елементах вищих порядків [5,6].
Але з таблиці 1 ми бачимо, що зберігається ваговий баланс: 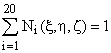 . Нефізичні флуктуації апріорних перехідних ймовірностей в сумі (2) „гасять” одна одну, тому розв’язок задачі практично співпадає з іншими підходами. Таблиця 2 показує, що вище зазначена заміна статистичних перехідних ймовірностей базисними функціями СЕ є виправданою.
. Нефізичні флуктуації апріорних перехідних ймовірностей в сумі (2) „гасять” одна одну, тому розв’язок задачі практично співпадає з іншими підходами. Таблиця 2 показує, що вище зазначена заміна статистичних перехідних ймовірностей базисними функціями СЕ є виправданою.
Для переконливості, результати, отримані за формулами (1) и (2), порівнюються з розв’язком кінцево-різницевим методом задачі Діріхлє для рівняння Лапласа (яким, як відомо, описується стаціонарна температура). Для цього була нанесена сітка з 27 внутрішніми вузлами і розв’язувалась система лінійних алгебраїчних рівнянь методом послідовного виключення невідомих (методом Гаусcа). Для отримання вектору правих частин значення температури на гранях були задані за допомогою усереднення заданих граничних умов.
Висновок. Всі три альтернативні моделі побудови температурного поля на скінченому елементі володіють властивістю стійкості, при цьому поліноміальна апроксимація розв’язку задачі значно скорочує і спрощує обчислення, без значної втрати точності, і виключає необхідність покриття СЕ сіткою.
3 alternative models of stationary temperature field in a cube are presented. They are statistical, analytical and grid. A statistical model is constructed with Monte Carlo averaging of temperature. An analytical model is constructed with polynomial interpolation. A grid model is constructed with finite – difference analogue of differential equation of Laplace.
1. Ермаков С.М., Михайлов Г.А. Курс статистического моделирования. –М.: «Наука», 1976. – 320 с.
2. Соболь И.М. Численные методы Монте-Карло. – М.: «Наука», 1973. – 312 с.
3. Манойленко О.С., Колесникова Н.В., Хомченко А.Н. Деякі узагальнення схеми випадкових блукань у мультиплексах // Труды Института прикладной математики и механики НАН Украины. - Т.6. - Донецк: ИПММ, 2001. - С. 75-79.
4. Манойленко О.С., Колесникова Н.В. Математична модель випадкових блукань у мультиплексі // Автоматика. Автоматизация. Электротехнические комплексы и системы. - №2(9), 2001. - С. 21-27.
5. Зенкевич О. Метод конечных элементов в технике./ Пер. с англ. под ред. Б.Е. Победри. – М.: Мир, 1975.- 544 с.
6. Манойленко О.С., Колеснікова Н.В. Блукання броунівської частинки у дискретному елементі зі штрафними маршрутами // Вестник ХГТУ. - №3(19), 2003. – С. 258-262.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.