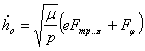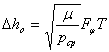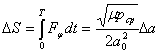Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 629.78

К ОПРЕДЕЛЕНИЮ ТРЕБОВАНИЙ К СИСТЕМАМ УВОДА КОСМИЧЕСКИХ ОБЪЕКТОВ

Дорошкевич В. К., Пироженко А. В., Хитько А. В., Хорольский П. Г.

Активное использование околоземного космического пространства обуславливает актуальность решение проблемы обеспечения увода космических объектов после завершения их эксплуатации с наиболее используемых орбит. Требования к ограничению засорения космического пространства определяют принятые Правила космической деятельности в Украине [1].

Задача увода КО во многом является новой задачей и ее решение связано с созданием специальных систем. Анализ возможных решений задачи увода и определение перспективных вариантов систем увода предполагают выработку требований к таким системам. Целью исследований, результаты которых изложены в данной статье, являлось определение предварительных требований к системам увода КО. Основанием для определения этих требований является анализ масс запускаемых космических аппаратов (КА), орбит их функционирования, требований к орбитам захоронения и срокам маневра увода КА [1], анализ энергетических затрат для выполнения маневров захоронения.

1. Анализ запусков КА по массам и орбитам

Анализ использования околоземного космического пространства искусственными объектами определяется для двух основных областей околоземных орбит: низких (НОО) с высотами до 2000 км и геостационарной (ГСО) высотой 36 тыс. км. Отдельно рассматривались средневысокие круговые (СКО) с высотами около 20 тыс. км и высокоэллиптические (ВЭО) с высотами апогея около 36 тыс. км, перигея – до 1000 км орбиты.

Анализ проводится на основе среднегодового количества выведенных и предполагаемых к запуску КА различных масс на различные типы орбит в период 2006 – 2011 гг.

Всего в период с 2006 по 2008 годы (по состоянию на 30.09.2008 г.) было выведено около 232 космических аппарата. Наибольшее количество КА было выведено на НОО и ГСО (124  и 72 космических аппарата, соответственно). А также было выведено на: СКО - 19 КА; ВЭО – 12 КА; межпланетные траектории – 5 КА.

Данные для статистики запусков космических аппаратов взяты из базы данных НКАУ "Технические характеристики и пуски существующих носителей мирового парка".

В таблицах 1 – 4 приведены среднестатистические данные по КА, выведенным в период 2006 – 2008 гг. На рисунке 1 показано количество выведенных КА на НОО и ГСО в период 2006-2008 гг. При этом, в таблице 1 приведено распределение количества КА по высотам орбит и годам, в таблице 2 и на рисунке 2 – распределение по массам и годам на НОО в период 2006-2008 гг., в таблице 3 — распределение количества КА по годам на ГСО, ВЭО, СКО в период 2006-2008 гг., в таблице 4 приведено распределение количества КА по массам и годам на ГСО.

Всего с 2006 по 2008 годы на НОО было выведено 124 КА (53 % от общего количества КА). В среднем в год ‑ 41,3 КА. Наибольшее количество КА было выведено на орбиту высотой до 800 км – 105 КА (85 % от количества выведенных КА на НОО).

Отметим, что из 124 КА, выведенных на НОО, 53 КА (43%) имеют массу до 100 кг.

Всего в 2006–2008 гг. на геостационарную орбиту было выведено 72 КА (31 % от общего количества КА). Из них всего 8 КА имеют массу до 2000 кг. Наибольшее количество КА имеют массу более 3500 кг (58 % от количества выведенных КА на ГСО).

Таблица 1

Распределение количества КА по высотам орбит и годам на НОО

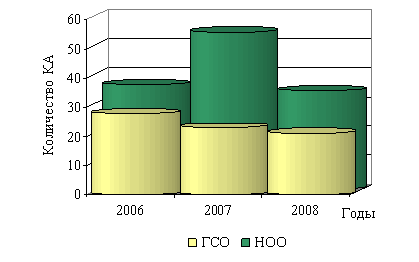
Рис. 1 Количество выведенных КА на НОО и ГСО в период 2006-2008 гг.

Таблица 2

Распределение количества КА по массам и годам на НОО

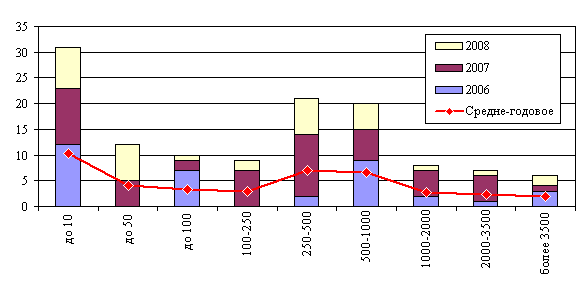
Рис. 2 Распределение количества КА по массам и годам на НОО

Таблица 3

Распределение количества КА по годам на ГСО, ВЭО, СКО

Таблица 4

Распределение количества КА по массам и годам на ГСО

Анализ прогноза запусков космических аппаратов в период 2009–2011 гг. показал, что в сравнении с периодом 2006–2008 гг. ситуация с запусками КА существенно не изменится.

2. Анализ требований к системам увода.

Поскольку задача увода КО является "сервисной" задачей, то естественным требованием к системам увода следует считать требование минимизации суммарных затрат на выполнение задачи. Эти затраты включают в себя затраты вывода на орбиту дополнительного груза, поддержание работоспособности системы увода весь срок целевого использования КО и сокращение времени целевого использования КО на время увода (для активных систем).

Интегрирование систем увода в качестве рабочих систем КО позволяет существенно повысить экономичность использования систем увода. Например, двигатели, используемые для увода КО, могут использоваться для управления ориентацией или орбитальным движением. Поэтому, определение требований к массе системы увода на предварительном этапе затруднено. Это связано также с тем, что для функционирования систем увода может потребоваться дополнительное оборудование КО, используемое при его целевом функционировании. Так, для работы электродвигателей требуются значительные ресурсы электроэнергии, обычно поступающей с солнечных батарей. Возможность использования «плановых» энергоресурсов, или необходимость увеличения площади батарей определяется во многом задачами функционирования КО.

Минимизация времени увода, также как и минимизация массы системы увода, не могут сами по себе определять требования к системам увода. Действительно, и то и другое являются лишь составляющими интегрального параметра – стоимости системы увода. Вместе с тем, представляется вполне оправданным, в качестве предварительных требований принять условие, чтобы время выполнения маневра увода не превосходило 10 % от времени планируемого целевого использования КО.

Рассмотрим требования к маневрам увода КО. Согласно Правилам космической деятельности в [1] ограничения на срок существования космической техники в регионах околоземного пространства после завершения ее эксплуатации распространяются только на район геостационарной орбиты и район низких орбит. Это, так называемые защищаемые регионы. Для КО, программа полета которых завершается в областях околоземного пространства, не входящих в состав защищаемых регионов, рекомендуется предусматривать выполнение маневров для сокращения их пребывания на орбите до сроков, сопоставимых с ограниченными сроками существования на НОО, или перемещение на орбиту захоронения, если они создают помехи в районах активно используемых орбит.

Защищаемый регион ГСО определяется как область околоземного пространства в виде кольцевого сегмента шара с параметрами:

– нижняя граница — высота геостационарной орбиты минус 200 км;

– верхняя граница — высота геостационарной орбиты плюс 200 км;

– границы по ширине — ± 15° от экваториальной плоскости;

– высота геостационарной орбиты — 35786 км.

Согласно [1] КА, прекратившие выполнение целевого назначения в защищаемом регионе ГСО, должны не позже, чем через один год после завершения эксплуатации, осуществить маневр перехода на орбиту захоронения.

Орбита захоронения должна располагаться выше защищаемого региона ГСО.

Значение высоты перигея орбиты захоронения должно удовлетворять неравенству

где        — разность между высотой перигея орбиты захоронения и высотой верхней границы защищаемого региона ГСО, км;

 — коэффициент давления солнечного излучения (типичные значения в диапазоне от 1 до 2);

 — облучаемая площадь КА, м²;

 — масса КА после завершения маневра перехода на орбиту захоронения и пассивации, кг;

1000 — удельный коэффициент, определяющий амплитуду колебаний высоты КА под действием силы давления солнечного излучения в окрестности верхней границы защищаемого региона ГСО, км×кг/м²;

35 — максимальное периодическое снижение уведенного на орбиту захоронения КА вследствие лунно-солнечных и геопотенциальных возмущений, км.

Требования к орбитальному переходу на орбиту захоронения ступеней РН и РБ, остающихся после выполнения целевого назначения в защищаемом регионе ГСО, те же, что и для КА.

На основании оценки формулы (1) можно считать, что требуемая высота перигея орбиты захоронения может не превосходить 300 км от высоты верхней границы защищаемого региона ГСО. Действительно, даже при сотнях метрах квадратных площади КА первое слагаемое в (1) не должно превосходить 200 км, так как масса такого КА ≥ 1000 кг. Конечно, существуют особые случаи конструкций КА, например пленочных отражателей, которые требуют дополнительных уточнений.

Таким образом, можно считать, что достаточным маневром увода КА с геостационарной орбиты является увеличение высоты перигея орбиты на 500 км за время не более года. Здесь предполагается, что время активного функционирования КА на ГСО равно приблизительно 10 лет.

Защищаемый регион низких околоземных орбит определяется как область околоземного космического пространства, расположенная ниже высоты 2000 км.

Согласно [1], при планировании и выполнении космических полетов должно обеспечиваться ограничение срока пребывания в защищаемом регионе НОО объектов космической техники, завершившие выполнение целевого назначения.

Рекомендованная предельная длительность пребывания в космическом пространстве КА и средств их выведения, которые остаются в защищаемом регионе НОО или периодически пересекают его границу после выполнения полетных заданий, равна 25 годам.

Для объектов космической техники, обладающих возможностью совершения орбитального маневра, основными вариантами уменьшения срока пребывания в защищаемом регионе НОО, являются:

– орбитальный переход, приводящий к входу в плотные слои атмосферы;

– переход с рабочей орбиты на орбиту с меньшим значением высоты перигея, на которой обеспечивается выполнения требования срока предельной длительности пребывания на НОО;

– переход на орбиту захоронения с перигеем, расположенным выше защищаемого региона НОО (в учетом последующей эволюции КО под действием возмущающих факторов).

Анализ интенсивности использования околоземного комического пространства искусственными объектами с учетом вышеизложенных требований, позволяет сделать следующие выводы. Для большего количества КО на НОО, высоты орбит которых лежат ниже 1000 км, маневр, заключающийся в изменении высоты перигея на 500 км в течение полугода, является достаточным для выполнения увода КО. Здесь предполагается, что КО на орбитах с перигеем ниже 550 км не будет существовать дольше 24 лет. Также предполагается, что время активного функционирования КО на НОО составляет приблизительно 6 лет. Увеличение высоты перигея орбиты на 500 км для КО на орбитах выше 1600 км представляются также достаточными для перевода КО на орбиты захоронения. Вместе с тем, для значительного количества КО, орбиты которых имеют высоту выше 1000 км и менее 1600 км потребуется более значительные изменения высот.

Оценим необходимый импульс управляющий силы для выполнения требуемых маневров. Для этого используем уравнение изменения энергии орбитального движения КО [2,3]

где        — приведенная к массе КО энергия его орбитального кеплерова движения;

 — гравитационная постоянная Земли;

, ,  — соответственно фокальный параметр, эксцентриситет и истинная аномалия орбиты КО;

,  — соответственно радиальное и трансверсальное ускорения, обусловленные действием сил, отличных от ньютоновской притягивающей силы.

Пренебрегая другими возмущающими ускорениями, будем считать, что  и  обусловлены действием двигательной установки. Из уравнения (2) видно, что изменение во времени интенсивности ускорений  и  позволяет, вообще говоря, повысить скорость изменения . При этом, изменения интенсивности должны быть в резонансе с изменением , и достигаемое повышение скорости изменения  пропорционально .

Отметим, что уравнение (2) можно записать в виде

где  — проекция управляющего ускорения на трансверсаль в перигее орбиты.

Для начальной круговой орбиты связь между изменением энергии  и импульсом постоянной управляющей силы, с точностью до , можно оценить по формуле

где        — некоторое среднее значение  за время маневра увода;

 — время маневра.

Оценка (4) в случае импульсного управления траекторией КА очевидна. Возможность использования (4) при постоянных малых управляющих ускорениях  и  следует из проведения операции усреднения уравнения (2) по угловой переменной .

Учитывая, что [2,3]

найдем, что требуемое

или с учетом того, что , т.е. пренебрегая  в степени выше первой,

Тогда оценка для удельного (отнесенного к массе КО) импульса силы имеет вид

На основании (4) получим оценки необходимых удельных импульсов управляющей силы для выполнения маневров увода, заключающегося в изменении  на 500 км. Для увода с НОО требуется удельный импульс около 270 м/с за время не более полугода. Для увода с ГСО требуется удельный импульс около 18 м/с за время не более года.

Приведенные оценки не содержат оценок изменения эксцентриситета. Вместе с тем, увод с НОО во многих случаях представляется целесообразным осуществлять путем снижения перигея орбиты до высот, обеспечивающих значительное аэродинамическое торможение КО. Для построения оценок изменения перигея орбиты рассмотрим простейший случай импульсного управления.

Для первоначально круговых орбит можно считать, что во время маневра <<1. Тогда, с точностью до , . Учитывая, что , где  – соответственно расстояние от центра Земли до перигея и апогея орбиты, и что  конечной орбиты равен радиусу исходной круговой, получим, что с точностью до

Таким образом, при импульсном управлении уменьшение высоты перигея приблизительно вдвое превосходит уменьшение , или, что тоже в рассматриваемом случае, величины фокального параметры орбиты. Т.е. при импульсном управлении снижение перигея орбиты потребует почти в 2 раза меньший импульс силы, чем аналогичное по величине снижение фокального параметра.

Выводы. Проведенные исследования позволили определить требования к энергетическим характеристикам систем увода КА с орбиты. Они показали, что для увода с низкой околоземной орбиты требуется удельный импульс силы около 270 м/с за время не более полугода. Для увода с геостационарной орбиты требуется удельный импульс силы около 18 м/с за время не более года. Эти результаты могут быть положены в основу баллистического проектирования КА с системами увода их с орбиты существования.

Перспективы дальнейших исследований состоят в уточнении рассмотренных требований применительно к конкретным КА и предполагаемым к применению двигательным установкам.

ЛИТЕРАТУРА

1.                  УРКТ-11.03. Правила космічної діяльності в Україні. Обмеження засмічення навколоземного космічного простору при експлуатації космічної техніки. – Київ: НКАУ, 2004. – 21 с.

2.                  Справочное руководство по небесной механике и астродинамике / Под ред. Г.Н. Дубошина. – М.: Наука, 1976. – 864 с.

3.                  Ротационное движение комических тросовых систем / А. П. Алпатов и др. – Днепропетровск : Институт технической механики НАН Украины и НКА Украины, 2001. — 404 с.