Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 62-50

АЛГОРИТМ АДАПТИВНОГО ОПРЕДЕЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ С ПОМОЩЬЮ ГАРМОНИЧЕСКОГО АНАЛИЗА

Гасанов А.С.

Введение

Математическое моделирование начинается с формализованного описания факторов и связей между ними, которые отражают течение технологического процесса. Построение различных математических моделей объектов производится на основе опытной информации о состоянии объекта (измерений) [1]. Среди них следует особенно выделить математические модели, которые строятся на основании гармонического анализа [2], поскольку, с увеличением количества членов разложения гармонического ряда может быть достигнуто сколь угодно малое различие между вычислениями модели и опытными данными (сколь угодно малые значения невязки). Однако, следует отметить, что на практике любые опытные данные измеряются с погрешностью. Кроме того, существуют стохастические колебания значений функции, которые не должны предсказываться в модели. Поэтому на практике нецелесообразно стремиться к сколь угодно малым значениям невязки.

С другой стороны, модель всегда лишь частично соответствует действительности, поэтому, когда поступает новая опытная информация, модель может быть откорректирована. Для этой цели может служить алгоритм Винера - Калмана [1]. Задачам построения адаптивных систем идентификации и управления посвящены также работы [3–5].

Целью настоящей работы является разработка алгоритма построения математической модели на основе гармонического анализа с применением адаптивных алгоритмов для уточнения параметров модели.

Постановка задачи

Рассмотрим метод построения математической модели объекта на основе гармонического анализа. Пусть требуется решить задачу прогнозирования значения функции  на отрезке . Введем отображение:

,                                                                       (1)

и введем функцию

,                                                  (2)

с областью определения . Тогда, как известно, такая функция может быть разложена в сходящийся бесконечный ряд вида [2]

            (3)

где коэффициенты , называемые коэффициентами Фурье, определяются формулами:

.

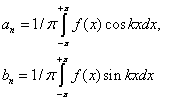Задача практического применения ряда Фурье сводится к представлению функции с помощью небольшого числа гармонических составляющих [6]. С помощью ряда Фурье можно аппроксимировать заданную функцию  на конечном интервале «равномерно хорошо» [2]. Это означает, что учитываются приближения функции во всех точках интервала.

Решение задачи

Рассмотрим процедуру определения коэффициентов ряда Фурье в выражении (3) с помощью метода наименьших квадратов (МНК). В точках измерений  значения модели:

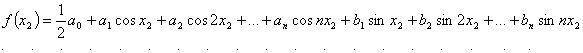
, (4)

где ое значение аргументов соответственно.

Введем обозначения  как разность между измеренным значением функции  и приближенным значением  при , т.е.

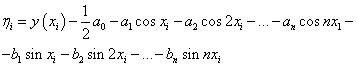                   (5)

Значения  и  находятся из условия минимума суммы квадратов отклонений

,

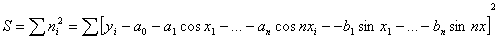где количество значений  и . Функция , как положительно определенная квадратичная форма, достигает минимума при

.

Выполнив дифференцирование в (4) получим систему алгебраических уравнений с равным количеством неизвестных  уравнений

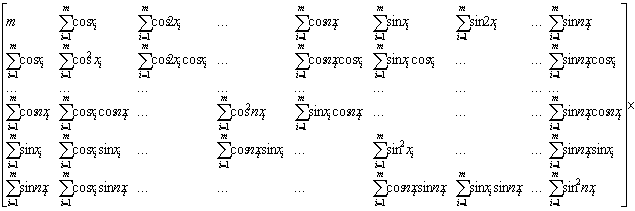
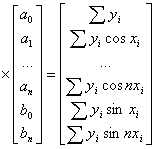                                                       (6)

Решив систему (6), найдем значения неизвестных параметров модели  и .

Рассмотрим теперь рекуррентные соотношения (фильтр Винера-Калмана [1,3]) для определения неизвестных параметров модели. Систему (4) представим в матричном виде:

или

,                                                               (7)

где . Произведя ое измерение из (7) получим , где

 ,

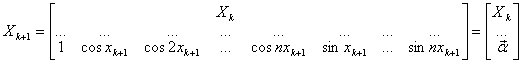
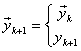Применяя рекуррентные формулы из [1] имеем:

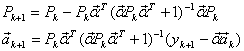,                                            (8)

Алгоритм построения математической модели с помощью гармонического анализа

Представим общий алгоритм построения и адаптации параметров математической модели объекта. Для построения математической модели объекта обычно используется опытная информация о состоянии объекта, которую можно использовать для априорного определения параметров модели [3]. Для этой цели в случае построения модели с помощью гармонического анализа можно использовать МНК (соотношения (6)). На рис. 1 представлен алгоритм построения математической модели объекта по априорным данным.

Алгоритм, представленный на рис. 1, состоит из следующих основных этапов.

1. Ввод исходных данных  и преобразование по формулам (1) и (2).

2. Вычисление нулевого члена разложения функции  (модели) в ряд Фурье. В качестве начального приближения можно взять среднее значение: .

3. Для следующего члена разложения в ряд Фурье проводится вычисление параметров по МНК.

4. Вычисляется невязка значений модели и исходной функции в точках измерений по формуле

,                                                             (9)

5. Если невязка удовлетворяет заданному критерию

,                                                                        (10)

то модель можно считать построенной. Если нет, – то добавляется еще один член ряда Фурье и заново проводится этап 3 вычисление невязки по формуле (9) и проверки условия (10).

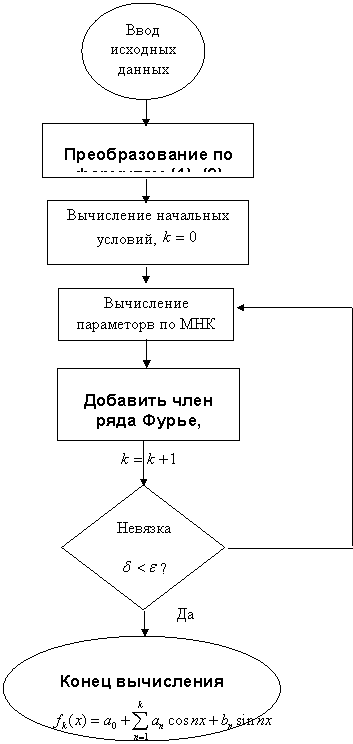Рис. 1. Алгоритм построения математической модели по априорным данным

Отметим, что на практике в связи со стохастическим характером функции и ошибками измерений не следует задавать слишком малым значение  в формуле (10). Значение  должно быть порядка величины среднеквадратической ошибки измерений.

Представим далее алгоритм уточнения математической модели в процессе прогнозирования и поступления новых данных (см. рис. 2).

В начале производится прогноз с помощью модели, построенной по априорным данным. Затем, при поступлении новых данных, производится адаптация параметров модели по Винеру-Калману (10) и производится новый прогноз. В дальнейшем, при поступлении новых данных цикл адаптации и прогнозирования повторяется.

Результаты расчетов

Проверим сходимость и устойчивость предложенного метода по определению неизвестных параметров  определяющих аппроксимацию временной зависимости , представленной в таблице 1, на интервале , где –интервал прогнозирования.

Таблица 1

Временная зависимость

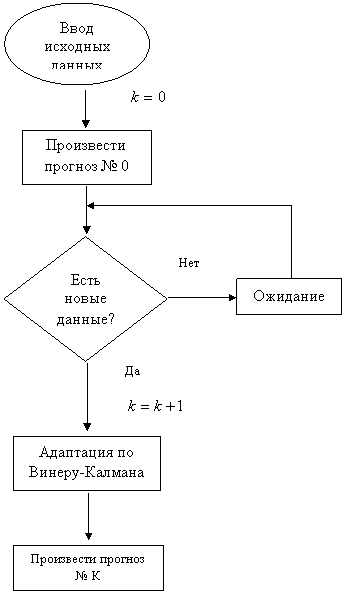Рис. 2 Адаптация параметров модели в процессе прогнозирования.

В данном случае будем считать, что априорные данные о представленной зависимости отсутствуют, и начальные значения параметров модели берутся произвольными.

Далее проведем вычисления параметров модели  по рекуррентным формулам (8), и проверим сходимость к апостериорным оценкам тех же параметров, полученных с помощью МНК по формулам (6) .

Вычисления проведем для случаев максимального количества членов разложения , то есть на примерах моделей, когда ряды Фурье имеют вид

;

;

.

На рис. 3, 4 показаны отклонения значений неизвестных параметров, вычисленных детерминированным МНК и адаптивным методом (по рекуррентным формулам (8)) при ,  в зависимости от количества измерений.

На этих рисунках по оси ординат отложена невязка (), а по оси абсцисс количество итераций.

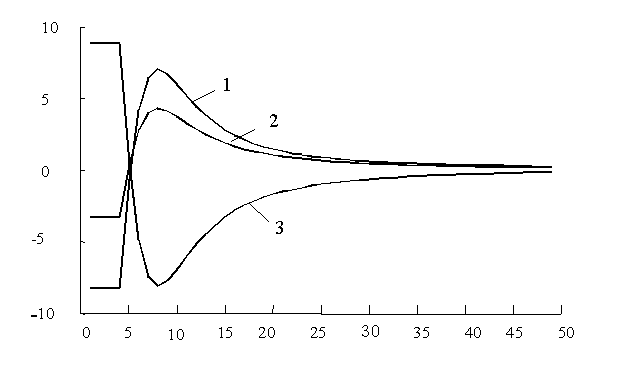
Рис. 3 Текущие отклонения параметров a₀ (кривая 1), a₁ (кривая 2), b₁ (кривая 3)

при  от рассчитанных по МНК

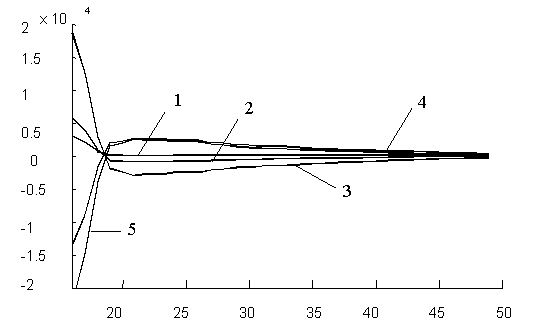
Рис. 4 Текущие отклонения параметров a₀ (кривая 1), a₁ (кривая 2), b₁ (кривая 3),

a₂ (кривая 4), b₂ (кривая 5) при  от рассчитанных по МНК

Анализ графиков свидетельствует о сходимости значений параметров, вычисленных при помощи адаптивных формул (8) к значениям, вычисленным a posteriori по МНК уже при количестве итераций, равной 50.

Заключение

Сформулирован алгоритм построения математической модели объекта с помощью гармонического анализа и адаптивного уточнения параметров. Используется алгоритм Винера-Калмана для адаптивного уточнения численных параметров математических моделей. Алгоритм применялся для построения математической модели зависимости, заданной таблицей 1. Бралось ограниченное количество членов ряда Фурье . Показана сходимость и устойчивость рекуррентных соотношений (8) к соотношениям, определяемым по МНК.

Таким образом, полученная математическая модель объекта, может быть использована в системе управления, в котором модель корректируется на каждом шаге измерения по формуле (8). При этом для корректировки модели на каждом шаге используется только последняя точка измерений.

1. Р. Ли. Оптимальные оценки, определение характеристик и управление.–М.: Наука, 1966.-176 с.

2. К. Ланцош. Практическое методы прикладного анализа. Справочное руководство / Под ред. А.М. Лопшица.–М.: Госфизматлит, 1961.–521 с.

3. Згуровский М.З., Подладчиков В.Н. Аналитические методы Калмановской фильтрации для систем с априорной неопределенностью.–К.: Наукова думка, 1995.–283 с.

4. Гасанов А.С. Адаптивные методы построения математических моделей объектов / Кибернетика и вычислительная техника.–2004.–№ 142.–С. 57-68.

5. Бидюк П.И., Гасанов А.С., Подладчиков В.Н. Прогнозирование значений параметров динамических систем с помощью адаптивного фильтра Калмана / Кибернетика и системный анализ.–2001.–№ 4.–С. 21–33.

6. Гасанов А.С. Адаптивные методы построения математических моделей объектов с помощью гармонического анализа / Международная научная конференция “Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий” (IDMIT'2005).–Евпатория: Херсонский морской институт, 2005.–Том 1.–С. 56–60.