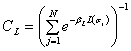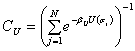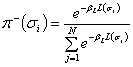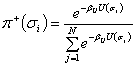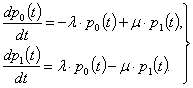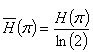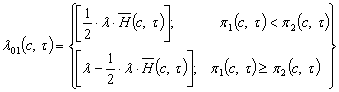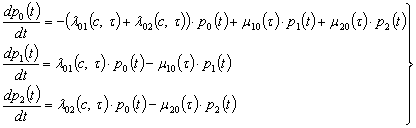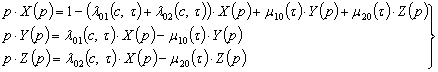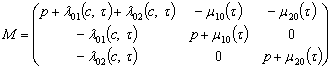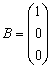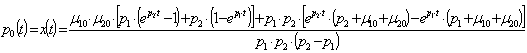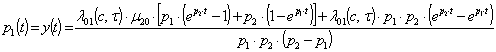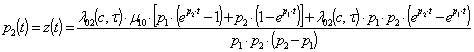УДК 62-843.6
МОДЕЛЮВАННЯ ВПЛИВУ ЕНТРОПІЇ СУБ’ЄКТИВНИХ ПЕРЕВАГ НА ПРИЙНЯТТЯ РІШЕНЬ СТОСОВНО РЕМОНТУ СУДНОВОЇ ЕНЕРГЕТИЧНОЇ УСТАНОВКИ
Гончаренко А.В.
Вступ та постановка проблеми. Ефективне керування складною транспортною системою, яку являє собою судноплавна компанія, потребує всебічного та адекватного аналізу інформаційних потоків, що надходять до неї. Функціонуючи в умовах постіндустріального, глобалізованого світу, насиченого сучасними, бурхливо розвинутими інформаційними технологіями, керівництво транспортної компанії, як правило, розглядає множину альтернатив можливого розвитку своєї діяльності. Таким чином, найчастіше, виникає ситуація невизначеності на фоні усвідомлення отриманої інформації.
Метою експлуатації транспортного судна, а також функціонування усієї системи є отримання прибутку при дотриманні вимог безпеки. Основні показники та критерії надійності та ефективності, а також правила їхнього вибору вказані у роботі [1].
Надійність техніки залежить, серед іншого, від своєчасності та якості технічного обслуговування та ремонту. Опрацювання науково обґрунтованого рішення, що приймається стосовно постановки судна в ремонт у ту чи іншу базу, у цілому, або суднової енергетичної установки (СЕУ), зокрема, відтак є актуальною задачею. При цьому мають бути враховані фактори інформаційного плану, невизначеності, а також наявних ресурсних можливостей та потреб експлуатації.
Аналіз останніх досліджень. Невизначеність при прийнятті управлінських рішень характеризується поняттям суб’єктивної ентропії, аналіз впливу якої на перебіг процесів, що відбуваються в активних техногенних системах розглядається в роботах [2-4].
У роботі [5] йдеться про доцільність прийняття управлінських економіко-організаційних рішень, надано їхні моделі, формалізовано критерії ефективності використання виробничого потенціалу.
Мета статті. Метою даної роботи є розробка математичної моделі, яка враховувала б у явному вигляді зв'язок між показниками надійності СЕУ та невизначеності при обранні бази для ремонту енергетичної установки судна.
Основний матеріал. Розглядається надійність та ефективність транспортного судна, пропонується математична модель, що описує, яким чином ентропія суб’єктивних переваг, як міра невизначеності, впливає на прийняття рішень стосовно ремонту СЕУ у відповідній базі. Однією з форм інформаційних технологій судноремонтного підприємства є подача відомостей про свою виробничу діяльність.
Постановка задачі. За умови, коли інформаційний потік досить ефективно й адекватно обробляється [6], керівництво судноплавної компанії має змогу, враховуючи наявні ресурси, необхідні для проведення поточного ремонту, обирати ту чи іншу базу. При цьому, виходячи з теоретичних міркувань [2, 4], суб’єкт формує власні переваги на множині досяжних для його цілей альтернатив із застосуванням функціоналу взятого у достатньо загальному вигляді [2, с. 119, (3.38)]:
|
|
(1) |
де Нπ – суб’єктивна ентропія; ε = ε(π, U, …) – функція суб’єктивної ефективності; N – нормуюча умова; α, β, γ – структурні параметри, котрі можуть розглядатися у різних ситуаціях як коефіцієнти Лагранжа, вагові коефіцієнти або ендогенні параметри, що відображають певні властивості психіки.
Обираючи функціонал (1) у вигляді [2, с. 124, (3.55)]:
|
|
(2) |
де ![]() – функція негативних переваг суб’єкта, стосовно досяжних для нього альтернатив
– функція негативних переваг суб’єкта, стосовно досяжних для нього альтернатив ![]() ;
; ![]() – функція втрат («шкідливості»); або [2, с. 125, (3.57)] у вигляді:
– функція втрат («шкідливості»); або [2, с. 125, (3.57)] у вигляді:
|
|
(3) |
де ![]() – функція суб’єктивних позитивних переваг;
– функція суб’єктивних позитивних переваг; ![]() – функція корисності, що має позитивний сенс; з необхідної умови екстремуму для випадків (2, 3):
– функція корисності, що має позитивний сенс; з необхідної умови екстремуму для випадків (2, 3):
|
|
|
отримуємо вирази:
|
|
(4) |
в яких коефіцієнти β й γ увійдуть відповідно як βL, γL – для функціоналу (2), коли до розгляду приймаються негативні якості обраної альтернативи ![]() ; та βU, γU – якщо ж суб’єктивну увагу, сформовану у вигляді функціоналу (3), привернуто до, можливо тих самих альтернатив, але врахуванню підлягають їхні позитивні якості.
; та βU, γU – якщо ж суб’єктивну увагу, сформовану у вигляді функціоналу (3), привернуто до, можливо тих самих альтернатив, але врахуванню підлягають їхні позитивні якості.
Звідси, з (4), буде:
|
|
(5) |
або, спрощуючи запис математичних виразів (5), для зручності трактовки математичної моделі, після введення відповідних констант:
|
|
(6) |
Використовуючи умови нормування, знайдемо константи ![]() ,
, ![]() , котрі входять до формул (6):
, котрі входять до формул (6):
|
|
(7) |
Тоді, підставляючи отримані константи в вирази для функцій суб’єктивних переваг, тобто формули (7) в (6), остаточно маємо:
|
|
(8) |
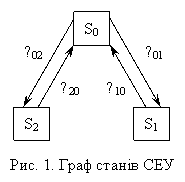
Тепер розглянемо найпростішу модель процесу виходу СЕУ на ремонт, в одну з двох можливих баз, у вигляді розміченого графу на три стани, показаного на рисунку 1. Тут Стан S0 відповідає стану СЕУ в експлуатації, S1, S2 – у ремонті в першій або другій судноремонтній базі відповідно. Інтенсивності переходів зі стану в стан позначені λ та μ. У даному випадку їх вважаємо величинами сталими у часі. Тобто ми маємо справу із випадковим процесом експлуатації СЕУ з дискретними станами та безперервним часом. Припускається, що перехід системи зі стану в стан відбувається миттєво, стрибкоподібним чином. Так само припущенням є й те, що такий перехід зі стану в стан буде можливим у будь-який довільний момент часу. Серед причин, які викликають зміну стану системи є фактори об’єктивні та суб’єктивні. Характеристики потоків подій приймаються відповідними до найпростішого, або стаціонарного пуасонівського.

Вибір судновласником підприємства 1 або 2, з метою проведення ремонтних операцій, здійснюється за умов певної невизначеності, яка моделюється у даній постановці задачі ентропією суб’єктивних переваг Нπ. Зміна ентропії вказує на обсяги інформації сприйнятої суб’єктом із загального потоку, що надходить до нього. Для грубої оцінки приймемо інформаційний потік безперервним, таким, що миттєво й адекватно сприймається. Залежно від ентропії суб’єктивних переваг ![]() , формується відносна величина невизначеності
, формується відносна величина невизначеності ![]() – відносна ентропія [2, с. 107, (3.19-3.22), с. 196, 197].
– відносна ентропія [2, с. 107, (3.19-3.22), с. 196, 197].
Причому, відношення ![]() береться до максимальної ентропії, що дорівнює логарифму від кількості можливих станів за умови віддання їм однакових переваг. Також враховується ставлення до ресурсів, задіяних у процесі ремонту, та отримуваних внаслідок останнього. Таким чином, невизначеність при прийнятті рішення враховує й складову сподівань суб’єкта на майбутній виграш від експлуатації більш надійної та досконалої техніки.
береться до максимальної ентропії, що дорівнює логарифму від кількості можливих станів за умови віддання їм однакових переваг. Також враховується ставлення до ресурсів, задіяних у процесі ремонту, та отримуваних внаслідок останнього. Таким чином, невизначеність при прийнятті рішення враховує й складову сподівань суб’єкта на майбутній виграш від експлуатації більш надійної та досконалої техніки.
При такій постановці, маємо алгоритм при прийнятті рішень щодо вибору потрібного судноремонтного заводу, у вигляді ланцюга, який включає в себе ланки відповідні до: ресурсів ![]() , через них до переваг
, через них до переваг ![]() , звідти до ентропійного блоку моделі
, звідти до ентропійного блоку моделі ![]() ,
, ![]() , який приймає участь у формуванні інтенсивностей відходу на ремонт λ01 та λ02 до відповідної бази. Характерним тут є те, що загальний потік λ, який переводить систему зі стану експлуатації у стан ремонту, розкладається на дві складові. Визначальну роль у розподілі λ на λ01 та λ02, у даній постановці задачі, відіграє порівняння функцій суб’єктивних переваг двох альтернативних судноремонтних підприємств та пропорційність відносній ентропії. Хоча можливими є й інші сценарії та мотиви техніко-економічної поведінки. На приклад, в постановці задачі в роботі [3, с. 53] складові, величини, що підлягає визначенню, формуються пропорційно відношенню функцій суб’єктивних переваг.
, який приймає участь у формуванні інтенсивностей відходу на ремонт λ01 та λ02 до відповідної бази. Характерним тут є те, що загальний потік λ, який переводить систему зі стану експлуатації у стан ремонту, розкладається на дві складові. Визначальну роль у розподілі λ на λ01 та λ02, у даній постановці задачі, відіграє порівняння функцій суб’єктивних переваг двох альтернативних судноремонтних підприємств та пропорційність відносній ентропії. Хоча можливими є й інші сценарії та мотиви техніко-економічної поведінки. На приклад, в постановці задачі в роботі [3, с. 53] складові, величини, що підлягає визначенню, формуються пропорційно відношенню функцій суб’єктивних переваг.
Тоді, отримуємо ймовірності знаходження системи СЕУ у відповідному стані. ![]() – ймовірність перебування в експлуатації: стан S0;
– ймовірність перебування в експлуатації: стан S0; ![]() – в ремонті на першому судноремонтному заводі: стан S1;
– в ремонті на першому судноремонтному заводі: стан S1; ![]() – в ремонті у другій базі: стан S2; як розв’язки системи диференційних рівнянь складених відповідно до графа, рис. 1, при заданих початкових умовах:
– в ремонті у другій базі: стан S2; як розв’язки системи диференційних рівнянь складених відповідно до графа, рис. 1, при заданих початкових умовах: ![]() ,
, ![]() ,
, ![]() (у початковий момент судно знаходиться в експлуатації), або
(у початковий момент судно знаходиться в експлуатації), або ![]() ,
, ![]() ,
, ![]() (у початковий момент судно на ремонті в першій базі), або інших, але з умовою нормування: сума ймовірностей:
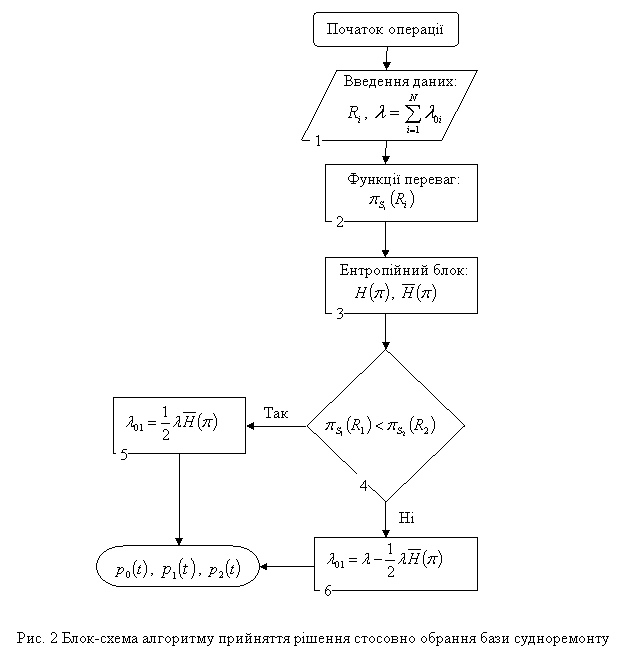
(у початковий момент судно на ремонті в першій базі), або інших, але з умовою нормування: сума ймовірностей: ![]() – для кожного моменту часу. Згаданий алгоритм прийняття рішення, заданий у вигляді фрагменту блок-схеми, показано на рисунку 2.
– для кожного моменту часу. Згаданий алгоритм прийняття рішення, заданий у вигляді фрагменту блок-схеми, показано на рисунку 2.

Розв’язання задачі. Якщо розглядати принципово можливі два стани СЕУ: 1) в експлуатації – S0, 2) в ремонті – S1, то граф зображений на рис. 1 набуває найпростішого вигляду з двома інтенсивностями потоків подій λ та μ. Система диференційних рівнянь має вигляд:
|
|
(9) |
Узявши похідну за часом від першого рівняння, і отримавши, таким чином, диференційне рівняння другого порядку до якого входить друге рівняння системи (9), будемо мати нову систему диференційних рівнянь з похідними лише від ![]() . Тобто систему з першим рівнянням системи (9) та новим отриманим рівнянням другого порядку.
. Тобто систему з першим рівнянням системи (9) та новим отриманим рівнянням другого порядку.
Від нової системи перейдемо до звичайного диференціального рівняння другого порядку лише з однією шуканою функцією, для якого, за допомогою складення й розв’язування характеристичного рівняння, отримаємо загальний розв’язок для першої невідомої функції. З нього, застосувавши математичні перетворення у зворотному напрямку, отримаємо загальний розв’язок для другої шуканої функції. Скориставшись початковими умовами знайдемо постійні інтегрування. При ![]() ,
, ![]() розв’язки будуть:
розв’язки будуть:
|
|
(10) |
Оскільки λ та μ, що входять до показників надійності (10) є сталими величинами у часі, то для графіків ймовірностей існують горизонтальні асимптоти, процес з часом стабілізується. Для ![]() асимптотою буде
асимптотою буде ![]() , для
, для ![]() –
– ![]() .
.
При можливості обрання однієї з двох баз для ремонту, граф буде таким як показано на рис.1. У випадку, коли суб’єктом оцінюються необхідні ресурси, потрібні для проведення чергового ремонту, і вони залежать від ціни та тривалості ремонту, то моделлю для ресурсів слугуватимуть вирази відповідно для першого та другого ремонтного підприємства:
|
|
(11) |
де с – ціна ремонту віднесена до часу, τ – тривалість ремонту, s1, s2 – ціна постановки СЕУ в ремонт відповідно в першу та другу базу, n1, n2 – коефіцієнти, які враховують ефективність проведення ремонту відповідно в першій та другій базі.
Алгоритм (рис.2, поз. 1) передбачає, також, врахування загальної інтенсивності потоку подій, що переводить систему СЕУ зі стану експлуатації у стан ремонту, як ![]() .
.
Функції суб’єктивних переваг сформовані за процедурою (1-8) з урахуванням ресурсів (11), відповідно до блок-схеми алгоритму рис. 2, поз. 2:
|
|
(12) |
Ентропія суб’єктивних переваг (рис. 2, поз 3)
|
|
(13) |
Відносна ентропія
|
|
(14) |
Розподіл загальної інтенсивності потоку подій переходу в ремонт λ, на відповідні λ01 та λ02, відбуватиметься з урахуванням функцій суб’єктивних переваг (12) і сформується пропорційно ступеню невизначеності у відносній формі (14). Тоді (рис. 2, поз. 4-6)
|
|
(15) |
Оскільки від тривалості ремонту залежатиме періодичність виходу суден з нього, то в даній постановці враховується, що інтенсивності потоків подій, які переводять систему СЕУ зі стану ремонту в стан експлуатації, є функціями тривалості ремонту. А саме ![]() ,
, ![]() .
.
Для варіанту з двома базами ремонту, рис. 1, отримуємо систему диференційних рівнянь (рівняння Ерланга):
|
|
(16) |
Для розв’язання системи (16) за початкових умов, у випадку коли інтенсивності потоків λ та μ є постійними величинами у часі, застосування інтегральних перетворень Лапласа видається більш привабливим з огляду на порівняну громіздкість попереднього методу для розв’язання (9) і отримання (10). При початкових умовах ![]() ,
, ![]() ,
, ![]() , перетворення Лапласа приводить до системи лінійних алгебраїчних рівнянь:
, перетворення Лапласа приводить до системи лінійних алгебраїчних рівнянь:
|
|
(17) |
де р – комплексний параметр; X(p), Y(p) та Z(p) – зображення (трансформанти) оригіналів (ймовірностей) ![]() ,
, ![]() та
та ![]() відповідно. Звідки з системи (16) маємо матрицю коефіцієнтів М та вектор-стовбець вільних членів В:
відповідно. Звідки з системи (16) маємо матрицю коефіцієнтів М та вектор-стовбець вільних членів В:
|
|
(18) |
Для трансформант, з (17, 18) отримуємо вирази:
|
|
(19) |
|
|
(20) |
|
|
(21) |
де ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Оригінали, відповідні до зображень (19-21):
|
|
(22) |
|
|
(23) |
|
|
(24) |
У формулах (22-24) для скорочення запису ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Практичне застосування розв’язку задачі. При розгляді трьох прикладів простежимо алгоритм прийняття рішення (рис. 2) та залежності (11-15, 22-24).
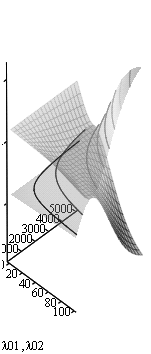
Приклад 1. Маємо дві незалежні змінні: 1) c – ціна ремонту віднесена до часу, та 2) τ – тривалість ремонту. Ресурси – функція від ціни та тривалості ремонту за моделлю (11), блок-схема алгоритму прийняття рішення рис. 2, поз. 1. Також від тривалості ремонту залежить частота виходу з нього. Припустимо, що інтенсивності виходу з ремонту для двох баз однакові. Інтенсивність виходу в ремонт у відповідну базу моделюється впливом ентропії суб’єктивних переваг (12-15), відповідно на рис. 2 поз. 2, 3. Розрахунки проведемо для наступних значень параметрів: c = 1∙102, 1,1∙102 … 5∙103, τ = 0,1 … 1∙102, s1 = 0,5∙104, s2 = 1∙104, n1 = 1,2∙10-1, n2 = 0,8∙10-1, β = 3∙10-4, λ = 2/300, μ10(τ) = μ20(τ) = 1/τ. Отримуємо усі проміжні залежності, як функції від двох незалежних змінних. У систему диференційних рівнянь (16) підставляємо інтенсивності λ01(с, τ), λ02(с, τ), отримані з (15), залежно від порівняння функцій переваг та відносної ентропії (рис.2, поз. 4-6), та μ10(τ), μ20(τ), але при певних значеннях незалежних змінних. Таким чином, після виконання (17-21) отримуємо ймовірності (22-24), як величини змінні у часі. Розрахунки проілюстровано тримірними графіками на рисунку 3 а), б). На рис 3 а) – відносну ентропію позначено Н1, вісь ентропії вертикальна, вісь τ спрямована у бік читача. На рис 3 б) координатні вісі незалежних змінних зорієнтовані подібним чином.
Приклад 2. Коли ціна та тривалість ремонту є функціями однієї незалежної змінної, часу t, то отримуємо за формулами (11-15) залежності від часу. У цьому прикладі моделі зміни цін на ремонт у часі у судноремонтних підприємствах c1(t), c2(t) різняться між собою. Зокрема, для першої бази судноремонту: ![]() , тут c10 – початковий рівень цін, k1 – коефіцієнт зростання ціни у часі. Для другої бази:
, тут c10 – початковий рівень цін, k1 – коефіцієнт зростання ціни у часі. Для другої бази: ![]() , сенс величин, що входять у цю формулу за змістом аналогічні до таких з попередньої формули. Моделі для інтенсивностей потоків подій виходу з ремонту μ10(t), μ20(t), передбачають обмеження підвищення зростання у межах досяжного рівня за даного розвитку техніки та технологій. Також враховується наявність різниці між підприємствами й за цим параметром. Відповідно для першого та другого судноремонтного підприємства:
, сенс величин, що входять у цю формулу за змістом аналогічні до таких з попередньої формули. Моделі для інтенсивностей потоків подій виходу з ремонту μ10(t), μ20(t), передбачають обмеження підвищення зростання у межах досяжного рівня за даного розвитку техніки та технологій. Також враховується наявність різниці між підприємствами й за цим параметром. Відповідно для першого та другого судноремонтного підприємства: ![]() ,
, ![]() , де Δ1 Δ2 – діапазони можливого підвищення інтенсивностей, m1, m2 – коефіцієнти, що спричиняють підвищення. Тривалості ремонтів відповідно:
, де Δ1 Δ2 – діапазони можливого підвищення інтенсивностей, m1, m2 – коефіцієнти, що спричиняють підвищення. Тривалості ремонтів відповідно: ![]() ,
, ![]() . Розрахунки за формулами (11-24) проведено для числових значень: t = 0 … 6∙102, s1 = 0,85∙104, s2 = 1∙104, n1 = 1,2∙10-1, n2 = 0,8∙10-1, β = 1,8∙10-2, c10 = 0,8∙103, k1 = 3,5, c20 = 1∙103, k2 = 1, Δ1 = 7∙10-2 m1 = 1∙10-2,37, Δ2 = 9∙10-2, m2 = 1,1∙10-2,9.
. Розрахунки за формулами (11-24) проведено для числових значень: t = 0 … 6∙102, s1 = 0,85∙104, s2 = 1∙104, n1 = 1,2∙10-1, n2 = 0,8∙10-1, β = 1,8∙10-2, c10 = 0,8∙103, k1 = 3,5, c20 = 1∙103, k2 = 1, Δ1 = 7∙10-2 m1 = 1∙10-2,37, Δ2 = 9∙10-2, m2 = 1,1∙10-2,9.
Приклад 3. Найбільш загальна постановка – коли ціни на ремонт та тривалості пов’язані між собою. Моделлю такого зв’язку слугують залежності: ![]() ,
, ![]() .
.
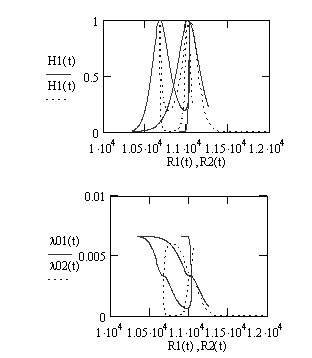
Дані для розрахунку використано з попереднього прикладу, окрім таких, що відрізняються від нього. А саме, у даному прикладі, відмінними є: c10 = 0,5∙103, Δ1 = 1,5∙10-1 m1 = 1∙10-5,85, Δ2 = 11∙10-2, m2 = 1,5∙10-5,12. Розрахунки проілюстровано фазовими портретами на рисунку 3 в), г).
У такій постановці передбачається, що існують суто об’єктивні обмеження для підвищення інтенсивностей виходу СЕУ з ремонту. Подальше, довготривале нарощування виробничих потужностей судноремонтних підприємств за рахунок інтенсифікації виробництва через збільшення затрачуваних на ремонт коштів є неможливим. Тому, так само, як і в попередньому прикладі, прийнята модель зростання частоти виходу з ремонту у відповідному діапазоні Δ1, Δ2. Відтак і тривалості ремонтів τ1(t), τ2(t) не є нескінченно малими величинами з плином часу.
У прикладах 2, 3 зроблено припущення про лінійних характер залежності цін на ремонт від часу, що є допустимим для початкової, наближеної постановки задачі. Суттєвим спрощенням у цілому, було також прийняття у постановці задачі стаціонарного пуасонівського потоку. Можливим варіантом розподілу загальної інтенсивності потоку λ є випадок, коли його складові формуються пропорційно відношенню функцій переваг.
На рис. 3 а) зображено залежності ентропії суб’єктивних переваг ![]() (нижчі значення), від ціни на ремонт с віднесеної до часу та тривалості ремонту τ; а також відносної ентропії
(нижчі значення), від ціни на ремонт с віднесеної до часу та тривалості ремонту τ; а також відносної ентропії ![]() ; б) – залежності інтенсивностей виходу з експлуатації в ремонт у відповідну базу
; б) – залежності інтенсивностей виходу з експлуатації в ремонт у відповідну базу ![]() ,
, ![]() , як функції від тих самих незалежних змінних; в) – фазові траєкторії відносної ентропії
, як функції від тих самих незалежних змінних; в) – фазові траєкторії відносної ентропії ![]() по ресурсах
по ресурсах ![]() та
та ![]() ; г) – фазові траєкторії у фазовому просторі фазових змінних
; г) – фазові траєкторії у фазовому просторі фазових змінних ![]() по
по ![]() , та
, та ![]() по
по ![]() .
.
На графіках фазових портретів, рис. 3 в), г) помітно, що коли відносна ентропія ![]() перебігає свої максимальні значення, розподіл інтенсивностей відбувається порівну
перебігає свої максимальні значення, розподіл інтенсивностей відбувається порівну ![]() . Наближення фазових траєкторій до замкнутих кривих говорить про тенденцію періодичності фазових змінних у часі.
. Наближення фазових траєкторій до замкнутих кривих говорить про тенденцію періодичності фазових змінних у часі.
в)

а) б) г)
Рис. 3 Залежності ентропії та інтенсивностей виходу СЕУ на ремонт
Висновки. У роботі розглянуто інформаційні аспекти проблеми управління постановкою СЕУ на ремонт в одну з двох можливих баз, а саме зв’язку невизначеності суб’єктивних переваг у вигляді відносної ентропії та інтенсивностей виходу СЕУ на ремонт. Розроблено математичну модель, яка на основі проблемно-ресурсного підходу показує можливість врахування впливу суб’єктивних переваг при прийнятті рішень керування через порівняння функцій переваг. Відповідно до отримуваної інформації суб’єкт схиляється до прийняття рішення про вибір ремонтної бази. Простежено причинно-наслідковий ланцюг ресурси, переваги, ентропія, інтенсивність виходу в ремонт до обраної бази. На основі положень суб’єктивного аналізу формується виваженість ефективної та надійної стратегії техніко-економічної поведінки відповідно до проблемно-ресурсні ситуації з урахуванням сприйнятої інформації.
The aspects of decision making concerning ship’s power plant repair depending on the uncertainty grade, modeled with the help of the subjective preferences entropy, are considered in the given article.
1. Надежность и эффективность в технике: Справочник: В 10 т. / Ред. совет: В.С. Авдуевский (пред.) и др. – М.: Машиностроение, 1988. – (В пер.). Т. 3. Эффективность технических систем / Под общ. ред. В.Ф. Уткина, Ю.В. Крючкова. – 328 с.
2. Касьянов В.А. Субъективный анализ: Монография. – К.: НАУ, 2007. – 512 с.
3. Касьянов В.А., Гончаренко А.В. Субъективный анализ и безопасность активных систем // Кибернетика и вычислительная техника. – 2004. – Вып. 142. – С. 41-56.
4. Касьянов В.А. Элементы субъективного анализа: Монография. – К.: НАУ, 2003. – 224 с.
5. Ареф’єва О.В., Михайленко В.М., Горяча О.Л. Моделі прийняття управлінських економіко-організаційних рішень підвищення ефективності використанні виробничого потенціалу та критерії доцільності їх застосування // Проблеми інформаційних технологій. – 2007. - №1. – С. 14-22.
6. Ходаков В.Е., Бардачев Ю.Н., Мартынов А.Н. Автоматизация и компьютеризация информационных процессов учреждений: учебное пособие. – Киев, Херсон, 1997. – 264 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Информационно-управляющие комплексы и системы
Теленик С.Ф., Ролік О.І., Букасов М.М., Андросов С.А. Генетичні алгоритми вирішення задач управління ресурсами і навантаженням центрів оброблення данихБогушевский В.С., Сухенко В.Ю., Сергеева Е.А., Жук С.В. Реализация модели управления конвертерной плавкой в системе принятия решений
Бень А.П., Терещенкова О.В. Применение комбинированных сетевых методов планирования в судоремонтной отрасли
Цмоць І. Г., Демида Б.А., Подольський М.Р. Методи проектування спеціалізованих комп’ютерних систем управління та обробки сигналів у реально-му час
Теленик С.Ф., РолікО.І., Букасов М.М., РимарР.В., Ролік К.О. Управління навантаженням і ресурсами центрів оброблення даних при виділених серверах
Селякова С. М. Структура інтелектуальної системи управління збиральною кампанією
Еременко А.П., Передерий В.И. Принятие решений в автоматизированных системах с учетом психофункциональных характеристик оператора на основе генетических алгоритмов
Львов М.С. Алгоритм перевірки правильності границь змінення змінних у послідовних програмах
Ляшенко Е.Н. Анализ пожарной опасности сосновых насаждений в зоне Нижне-днепровских песков – самой большой пустыни в Европе
Кучеров Д.П., Копылова З.Н. Принципы построения интеллектуального автору-левого
Касаткина Н.В., Танянский С.С., Филатов В.А. Методы хранения и обработки нечетких данных в среде реляционных систем
Ходаков В.Е., Жарикова М.В., Ляшенко Е.Н. Применение когнитивного подхода для решения задачи поддержки принятия управленческих решений при ликвидации лесных пожаров
Фарионова Н.А. Системный подход построения алгоритмов и моделей систем поддержки принятия решений при возникновении нештатных ситуаций
Биленко М.С., Серов А.В., Рожков С.А., Буглов О.А. Многоканальная система контроля качества текстильных материалов
Мотылев K.И., Михайлов M.В., Паслен В.В. Обработка избыточной траекторной информации в измерительно-вычислительных системах
Гончаренко А.В. Вплив суб’єктивних переваг на показники роботи суднової енергетичної установки
Гульовата Х.Г., Цмоць І.Г., Пелешко Д.Д. Архітектура автоматизованої системи моніторингу і дослідження характеристик мінеральних вод
Соломаха А.В. Разработка метода упреждающей компенсации искажений статорного напряжения ад, вносимых выходными силовыми фильтрами
ПотапенкоЕ.М., Казурова А.Е. Высокоточное управление упругой электромеханической системой с нелинейным трением.
Кузьменко А.С., Коломіц Г.В., Сушенцев О.О. Результати розробки методу еквівалентування функціональних особливостей fuzzy-контролерів
Кравчук А. Ф., Ладанюк А.П., Прокопенко Ю.В. Алгоритм ситуационного управления процессом кристаллизации сахара в вакуум-аппарате периодического действия с механическим циркулятором
Абрамов Г.С., Иванов П.И., Купавский И.С., Павленко И.Г. Разработка навигационного комплекса для автоматического наведения на цель системы груз-управляемый парашют
Литвиненко В.И., Четырин С.П. Компенсация ошибок оператора в контуре управления следящей системы на основе синтезируемых вейвелет-сетей
Бардачев Ю.Н., Дидык А.А. Использование положений теории опасности в искусственных иммунных системах
Рожков С.О., Кузьміна Т.О., Валько П.М. Інформаційна база як основа для створення асортименту лляних виробів.
Ускач А.Ф., Становский А.Л., Носов П.С. Разработка модели автоматизированной системы управления учебным процессом
Мазурок Т.Л., Тодорцев Ю.К. Актуальные направления интеллектуализации системы управления процессом обучения.
Ускач А.Ф., Гогунский В.Д., Яковенко А.Е. Модели задачи распределения в теории расписания.
Сідлецький В.М., Ельперін І.В., Ладанюк А.П. Розробка алгоритмів підсистеми підтримки прийняття рішень для контролю якості роботи дифузійного відділення.
Пономаренко Л.А., Меликов А.З., Нагиев Ф.Н. Анализ системы обслуживания с различными уровнями пространственных и временных приоритетов.
Коршевнюк Л.О. Застосування комітетами експертів системи нечіткого логічного виводу із зваженою істинністю.. – С. 73 – 79.
Кирюшатова Т.Г., Григорова А.А Влияние направленности отдельных операторов и направленности всей группы на конечный результат выполнения поставленной задачи.
Петрушенко А.М., Хохлов В.А., Петрушенко І.А. Про підключення до мови САА/Д деяких засобів паралельного програмування пакету МРІСН.
Ходаков В.Е., Граб М.В., Ляшенко Е.Н. Структура и принципы функционирования системы поддержки принятия решений при ликвидации лесных пожаров на базе новых геоинформационных технологий.
Сидорук М.В., Сидорук В.В. Информационные системы управления корпорацией в решении задач разработки бюджета.
Нагорный Ю.И. Решение задачи автоматизированного расчета надежности иасуп с использованием модифицированного метода вероятностной логики
Козак Ю.А. Колчин Р.В. Модель информационного обмена в автоматизированной системе управления запасами материальных ресурсов в двухуровневой логистической системе
Гожий А.П., Коваленко И.И. Системные технологии генерации и анализа сценариев
Вайсман В.А., Гогунский В.Д., Руденко С.В. Формирование структур организационного управления проектами
Бараненко Р.В., Шаганян С.М., Дячук М.В. Аналіз алгоритмів взаємних виключень критичних інтервалів процесів у розподілених системах
Бабенко Н.И., Бабичев С.А. Яблуновская Ю.А. Автоматизированная информационная система управления учебным заведением
Яковенко А.Е. Проектирование автоматизированных систем принятия решений в условиях адаптивного обучения с учетом требований болонского процесса
Бараненко Р.В Лінеаризація шкали і збільшення діапазону вимірювання ємностей резонансних вимірювачів
Головащенко Н.В. Математичні характеристики шумоподібно кодованих сиг-налів.
Шерстюк В.Г. Формальная модель гибридной сценарно-прецедентной СППР.
Шекета В.І. Застосування процедури Append при аналізі абстрактних типів даних модифікаційних запитів.
Цмоць І.Г. Алгоритми та матричні НВІС-структури пристроїв ділення для комп'-ютерних систем реального часу.
Кухаренко С.В., Балтовский А.А. Решение задачи календарного планирования с использованием эвристических алгоритмов.
Бараненко Р.В., Козел В.Н., Дроздова Е.А., Плотников А.О. Оптимизация рабо-ты корпоративных компьютерных сетей.
Нестеренко С.А., Бадр Яароб, Шапорин Р.О. Метод расчета сетевых транзакций абонентов локальных компьютерных сетей.
Григорова А.А., Чёрный С. Г. Формирование современной информационно-аналитической системы для поддержки принятия решений.
Шаганян С.Н., Бараненко Р.В. Реализация взаимных исключений критических интервалов как одного из видов синхронизации доступа процессов к ресурсам в ЭВМ
Орлов В.В. Оценка мощности случайного сигнала на основе корреляционной пространственной обработки
Коджа Т.И., Гогунский В.Д. Эффективность применения методов нечеткой логики в тестировании.
Головащенко Н.В., Боярчук В.П. Аппаратурный состав для улучшения свойств трактов приёма – передачи информации в системах промышленной автоматики.