УДК 519.63:539.3
МОДЕЛИРОВАНИЕ ТРАНСЛЯЦИОННЫХ ФУНКЦИЙ
ФОРМЫ НА ГЕКСАГОНЕ
Хомченко А.Н. , Моисеенко С.В. , Цыбуленко О.В.
Постановка проблемы, анализ предшествующих публикаций
Дискретный элемент в форме правильного шестиугольника (гексагона) с узлами интерполяции в вершинах широко применяется в расчетах ядерных реакторов и других конструкций с фрагментами сотовой геометрии [1,2]. Попытка построить средствами матричной алгебры стандартный шестипараметрический полином, решающий задачу лагранжевой интерполяции на гексагоне, оказалась неудачной [1], так как привела к вырождению СЛАУ. Эта особенность гексагона стимулировала развитие геометрических подходов к построению гексагональных функций формы. Именно благодаря геометрическому моделированию появился дробно-рациональный базис гексагона [1,3], а вскоре и полиномиальный [4]. В работе [5] впервые показана возможность распространения геометрического моделирования на полиномиальные базисы гексагонов высших порядков.
Геометрическое конструирование на гексагоне полиномиальной функции формы, как правило, приводит к появлению “лишних” членов высших порядков, что вызывает аномальное поведение базисной функции внутри гексагона и/или на его границе. В некоторых случаях такие аномалии не имеют нежелательных последствий благодаря полному или частичному сглаживанию при ансамблировании функций формы [2]. В других случаях [3] могут потребоваться специальные приемы нормализации “базиса” для создания необходимых интерполяционных качеств и вычислительных свойств модели.
Цель работы – проиллюстрировать возможность геометрического конструирования системы полиномиальных функций формы, решающих задачу лагранжевой интерполяции на гексагоне по известным значениям искомой функции в вершинах элемента. Гексагон рассматривается как самостоятельный вычислительный шаблон, оснащенный унитарным набором функций формы для восстановления финитной полевой функции. Поэтому традиционные для МКЭ вопросы ансамблирования элементов и межэлементной непрерывности здесь не рассматриваются.
Основная часть. В плоскости 0ху рассмотрим правильный шестиугольник, вписанный в окружность единичного радиуса с центром в начале координат (рис.1).
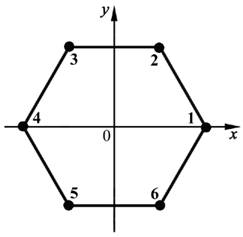
Рис.1 Гексагональный элемент с 6-ю узлами
Главная задача заключается в построении набора из шести полиномов pi(x,y), удовлетворяющих интерполяционной гипотезе Лагранжа:
![]()
![]() (1)
(1)
где ![]() - символ Кронекера.
- символ Кронекера.
Мы начнем построение с функции р1(х,у),
которая ассоциируется с узлом 1(1;0). Из условий (1) следует, что эта функция
равна единице в “своём” узле и нулю в остальных узлах. Геометрически р1(х,у)
– это поверхность, “нависающая” над гексагоном и образованная перемещением
(трансляцией) выпуклой параболы ![]() по вогнутой
параболе
по вогнутой
параболе ![]() Такие поверхности в теории
конструкционных оболочек называют трансляционными. Таким образом, мы получаем
первую функцию в виде:
Такие поверхности в теории
конструкционных оболочек называют трансляционными. Таким образом, мы получаем
первую функцию в виде:
![]() .
(2)
.
(2)
Остальные функции получаются из (2) вращением системы координат на угол, кратный 600. На рис.2 показана функция р1(х,у).
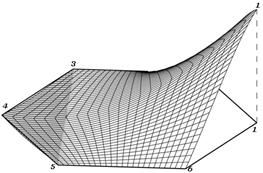
Рис.2 График функции р1(х,у)
Заметим, что поверхности р1(х,у) и р4(х,у)симметричны относительно координатной плоскости у=0. Вообще, поверхность рі(х,у) симметрична относительно вертикальной диагональной плоскости, проходящей через узел і и центр гексагона. Все функции рі(х,у) одинаковы, что является следствием симметрии гексагона. При безусловном соблюдении интерполяционной гипотезы всё же имеет место нарушение весового баланса в системе трансляционных функций формы. Подобный недостаток был обнаружен в несовершенной системе полиномов Ишигуро [1,3]. Однако, в отличие от сильно избыточной модели Ишигуро, здесь дисбаланс гораздо слабее
![]() (3)
(3)
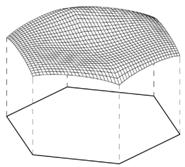
Рис.3. Сумма функций формы гексагона
Рис.3 дает наглядное представление об отклонениях суммы (3) от стандарта. Как видим, трансляционный базис практически не отличается от синтетического [6], что позволяет рассчитывать на практическую пригодность построенной системы функций. Ясно, что в большинстве задач интерполяции потенциального поля трансляционный базис будет давать вполне приемлемые результаты. В условиях повышенных требований к точности вычислений можно нормализовать трансляционный базис с целью полного устранения дисбаланса, как это было сделано с полиномами Ишигуро [1,3]. Правда, в этом случае нормирующий множитель должен обеспечить немонотонное сжатие поверхности (рис.3) к плоскости 0ху. Ясно, что это приведет к новому дробно-рациональному базису.
Выводы. Идея разделения переменных в интерполяционном коэффициенте Лагранжа р1(х,у) дает простой и наглядный способ конструирования трансляционных функций формы на гексагоне. Слабое нарушение весового баланса не влияет существенно на вычислительные качества модели и при необходимости может быть устранено с помощью функционального нормирующего множителя. Возникающий при этом новый дробно-рациональный базис будет описан в последующих публикациях.
The possibility of geometrical model operation of translating basis functions such as the Lagrange for restitution of a potential field on hexagon is explored. The appearance feeble weight dizbalance in a system of functions of the shape is analyzed.
1. Ishiguro M. Construction of hexagonal basis functions applied in the Galerkin-type finite element method // J. Inf. Process. 1984. V. 7, №2. – P.89-95.
2.
Хомченко А.Н. К расчету
температурных полей в сотовых структурах методом конечных элементов //
Инж.-физ. журнал. – 1987. – Т.52, №2. –
С.301-305.
3. Хомченко А.Н. О дробно-рациональной интерполяции на шестиугольном конечном элементе//Вісник Запорізького Державного університету (Серія: фізико-математичні науки).-2002.-№3.-С.84-84.
4. Хомченко А.Н. Об одном проекционно-сеточном алгоритме вычислительной механики // VI Всесоюз. съезд по теор. и прикл. механике: Аннот. докл .- Ташкент, 1986.-С.628-629.
5. Гучек П.И., Литвиненко Е.И., Хомченко А.Н. Геометрическое моделирование полиномиальных базисов гексагональных конечных элементов // Матем. моделирование. - К.: Институт математики НАМ Украины, 1996.-С.84-87.
6. Хомченко А.Н. Синтетична модель гексагонального скінченного елемента // Прикладна геометрія та інженерна графіка. Праці / Тавр. держ. агротехн. академія. – Вип.4, т.20. – Мелітополь: ТДАТА, 2003.- С.9-13.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.