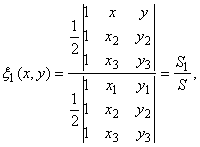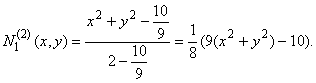УДК 519.2: 519.3
ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ ЭЛЕМЕНТОВ С КРИВОЛИНЕЙНЫМИ ГРАНИЦАМИ
Хомченко А.Н., Козуб Н.А.
Постановка проблемы. В большинстве сеточных методов (например, в МКР, МКЭ) используются в основном ячейки с прямыми сторонами. Между тем, в реальных задачах границы области и линии раздела материалов часто изогнуты. Поэтому важной проблемой МКЭ является построение базисных функций для сеток, составленных из элементов с криволинейными сторонами. Если некоторая часть границы или линии раздела изогнута, весьма удобны прямоугольные треугольники с двумя прямыми и одной криволинейной сторонами. Именно такие треугольники (с изогнутой гипотенузой) играют определяющую роль при геометрическом моделировании базисных функций плохо поддающихся какой-либо формализации серендиповых элементов высших порядков.
Анализ предшествующих публикаций, постановка задачи. Впервые криволинейный элемент появился в расчетах инженерных сооружений у авторов [1]. Комментарий по этому вопросу есть у Зенкевича [2], а некоторые конкретные результаты у авторов [3]. Установление в 1982 г. вероятностного смысла базисных функций МКЭ [4] способствовало проникновению геометрического моделирования в теорию интерполирования функций двух и трех аргументов на конечных носителях [5,6]. Накопленный опыт моделирования базисов КЭ показывает, что криволинейные границы не создают специфических трудностей, если пользоваться концепцией геометрической вероятности. При этом для полиномиальных базисов достаточно ограничиться фрагментами кривых второго порядка (окружность, эллипс, парабола, гипербола). Мы рассмотрим прямоугольный треугольник с криволинейной гипотенузой. Наша цель – на основе кривых второго порядка построить в явном виде набор базисных функций для узла в вершине прямого угла. С помощью такого набора легко генерировать классические и новые базисы серендиповых элементов высших порядков.
Основная часть. Вначале стоит обратить внимание на свойства базисных функций КЭ. Для этого достаточно рассмотреть самые простые двумерные элементы: треугольник с 3-мя узлами (рис.1а), реализующий линейную интерполяцию, и квадрат с 4-мя узлами (рис. 1б), реализующий билинейную интерполяцию функции двух аргументов.
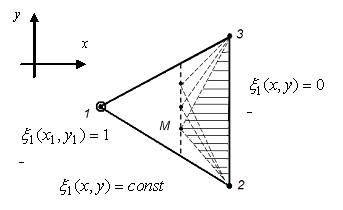
а) б)
Рис.1 Конечные элементы линейной а) и билинейной б) интерполяции
Для определенности на каждом КЭ рассматривается узел 1. Известно [3], что базис линейной интерполяции состоит из барицентрических координат симплекса. Первая координата определяется формулой
|
|
(1) |
где S – площадь основного треугольника 1-2-3; S1- площадь треугольника М-2-3; М(x,y) – текущая точка. Как видим, ![]() - это вероятность попадания случайной точки в треугольник М-2-3 (заштрихован) при вбрасывании этой точки в основной треугольник 1-2-3. Вершины множества треугольников М-2-3 одинаковой площади S1 лежат на линии уровня
- это вероятность попадания случайной точки в треугольник М-2-3 (заштрихован) при вбрасывании этой точки в основной треугольник 1-2-3. Вершины множества треугольников М-2-3 одинаковой площади S1 лежат на линии уровня ![]() . Это «текущая» линия уровня. Понятно, что все линии уровня
. Это «текущая» линия уровня. Понятно, что все линии уровня ![]() параллельны прямой 2-3, т.е. прямой
параллельны прямой 2-3, т.е. прямой ![]() . Перемещение линии уровня к «собственному» узлу 1 сопровождается равномерным возрастанием аппликаты от 0 до 1, т.е.
. Перемещение линии уровня к «собственному» узлу 1 сопровождается равномерным возрастанием аппликаты от 0 до 1, т.е. ![]() . Таким образом, достаточно составить уравнение границы «входа» в область КЭ со стороны, противолежащей узлу 1. Это уравнение линии нулевого уровня. Для получения соответствующей базисной функции уравнение линии нулевого уровня необходимо пронормировать так, чтобы
. Таким образом, достаточно составить уравнение границы «входа» в область КЭ со стороны, противолежащей узлу 1. Это уравнение линии нулевого уровня. Для получения соответствующей базисной функции уравнение линии нулевого уровня необходимо пронормировать так, чтобы ![]() .
.
Аналогичная ситуация отражена на рис.1б. Теперь вероятность попадания случайной точки в прямоугольник с противоположными вершинами М-3 равна
|
|
(2) |
Билинейный полином «чуть старше» линейного за счет дополнительного слагаемого xy. Это слагаемое вносит некоторые особенности в поведение функции ![]() . Теперь при стремлении текущей точки М(x,y) к узлу 1 равномерное возрастание
. Теперь при стремлении текущей точки М(x,y) к узлу 1 равномерное возрастание ![]() отмечается только в координатных направлениях. В произвольном направлении возрастание неравномерное, так как
отмечается только в координатных направлениях. В произвольном направлении возрастание неравномерное, так как ![]() представляет собой фрагмент поверхности второго порядка – гиперболического параболоида (гипара).
представляет собой фрагмент поверхности второго порядка – гиперболического параболоида (гипара).
Основной вывод таков: независимо от геометрии поверхности базисная функция в текущей точке М(x,y) определяет относительный подъем текущего уровня.
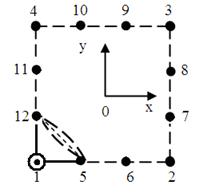
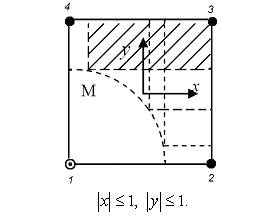
Теперь можно генерировать альтернативные базисы на серендиповых КЭ высших порядков за счет вариации профиля искривленной гипотенузы в прямоугольном треугольнике. В качестве примера мы рассмотрим серендипов элемент с бикубической интерполяцией (рис.2). Предполагается, что 12 узлов распределены равномерно на границе КЭ.
|
|
Рис.2 Серендипов КЭ с бикубической интерполяцией
Построить модель бикубической интерполяции означает сконструировать 12 полиномов с двумя аргументами, удовлетворяющих интерполяционной гипотезе типа Лагранжа:
|
|
(3) |
где ![]() – номер полинома;
– номер полинома; ![]() – номер узла (
– номер узла (![]() );
); ![]() - символ Кронекера. Кроме того, должны соблюдаться условия межэлементной непрерывности. Это означает, что полином
- символ Кронекера. Кроме того, должны соблюдаться условия межэлементной непрерывности. Это означает, что полином ![]() на границе, содержащий узел i, должен изменяться по закону кубической параболы (4 узла). На остальных границах КЭ
на границе, содержащий узел i, должен изменяться по закону кубической параболы (4 узла). На остальных границах КЭ ![]() обращается в нуль. При регулярном расположении узлов достаточно построить только два полинома, например,
обращается в нуль. При регулярном расположении узлов достаточно построить только два полинома, например, ![]() и
и ![]() . Мы остановим свой выбор на более содержательном полиноме -
. Мы остановим свой выбор на более содержательном полиноме - ![]() . Не потому, что узел 1 объединяет вдвое больше соседних элементов, нежели узел 5. А прежде всего потому, что в этом случае востребованы прямоугольные треугольники с искривленной гипотенузой. Мы исходим из того, что искомый полином
. Не потому, что узел 1 объединяет вдвое больше соседних элементов, нежели узел 5. А прежде всего потому, что в этом случае востребованы прямоугольные треугольники с искривленной гипотенузой. Мы исходим из того, что искомый полином ![]() можно представить в виде произведения нескольких полиномов первого и второго порядков. Из этого следует, что сложный серендипов элемент высокого порядка можно представить в виде композиции из простых элементов с общим узлом 1. На простом элементе нетрудно построить подходящий полином первого или второго порядка. При этом линиями пулевого уровня являются прямолинейные отрезки или фрагменты стандартных кривых второго порядка (рис.2). Возможности геометрического моделирования мы иллюстрируем на треугольнике 1-5-12. Заметим, что существуют модели бикубических серендиповых элементов, использующие другие треугольники, например, 1-6-11, 1-6-12, 1-5-11.
можно представить в виде произведения нескольких полиномов первого и второго порядков. Из этого следует, что сложный серендипов элемент высокого порядка можно представить в виде композиции из простых элементов с общим узлом 1. На простом элементе нетрудно построить подходящий полином первого или второго порядка. При этом линиями пулевого уровня являются прямолинейные отрезки или фрагменты стандартных кривых второго порядка (рис.2). Возможности геометрического моделирования мы иллюстрируем на треугольнике 1-5-12. Заметим, что существуют модели бикубических серендиповых элементов, использующие другие треугольники, например, 1-6-11, 1-6-12, 1-5-11.
В многочисленных публикациях по МКЭ упоминается лишь один бикубический базис, изобретательно подобранный Эргатудисом, Айронсом и Зенкевичем [2]. Мы покажем, как устроен этот классический базис и приведем примеры альтернативных (неклассических) базисов бикубической интерполяции. Для построения классического полинома ![]() мы представляем КЭ-12 (рис.2) в виде композиции из основного квадрата 1-2-3-4 и встроенного треугольника 1-5-12 с общим (это важно) узлом в вершине 1. Основной квадрат входит в состав всех без исключения серендиповых моделей, а модификации можно получить изменяя форму гипотенузы встроенного треугольника. В данном случае в качестве гипотенузы 5-12 мы используем дугу окружности с центром в (0;0).
мы представляем КЭ-12 (рис.2) в виде композиции из основного квадрата 1-2-3-4 и встроенного треугольника 1-5-12 с общим (это важно) узлом в вершине 1. Основной квадрат входит в состав всех без исключения серендиповых моделей, а модификации можно получить изменяя форму гипотенузы встроенного треугольника. В данном случае в качестве гипотенузы 5-12 мы используем дугу окружности с центром в (0;0).
Итак, на квадрате в соответствии с формулой (2) относительное приращение текущего уровня равно
|
|
На треугольнике относительное приращение текущего уровня равно
|
|
Заметим, что ![]() - квадрат радиуса текущей окружности;
- квадрат радиуса текущей окружности; ![]() - квадрат радиуса окружности нулевого уровня, проходящей через узлы 5 и 12; 2=R2- квадрат радиуса окружности максимального уровня, проходящей через узел 1. Если числитель и знаменатель последней формулы умножить на
- квадрат радиуса окружности нулевого уровня, проходящей через узлы 5 и 12; 2=R2- квадрат радиуса окружности максимального уровня, проходящей через узел 1. Если числитель и знаменатель последней формулы умножить на ![]() , легко усмотреть отношение «текущей» площади кольца к максимальной площади кольца. Неудивительно, что мы снова пришли к геометрической вероятности. Окончательно, мы получаем [2]
, легко усмотреть отношение «текущей» площади кольца к максимальной площади кольца. Неудивительно, что мы снова пришли к геометрической вероятности. Окончательно, мы получаем [2]
|
|
Окружность нулевого уровня, как легко заметить, проходит через все промежуточные узлы, хотя необходимость в этом имеется только в узлах 6 и 11. В узлах 7,8,9,10 возникают нежелательные кратные нули, которые усиливают жесткость модели. Другой недостаток этой модели – «негативизм» спектра узловых нагрузок от равномерной массовой силы. Существует ошибочное мнение, что на КЭ высших порядков «негативизм» неустраним. Следующая модель опровергает это мнение.
Эта модель состоит из основного квадрата и двух вложенных треугольников с прямолинейными гипотенузами: 1-5-12 и 1-6-11. Относительное приращение текущего уровня на треугольнике 1-5-12 равно
|
|
Эта функция определяет вероятность попадания в треугольник М-5-12 случайной точки, вброшенной в треугольник 1-5-12.
Относительное приращение текущего уровня на треугольнике 1-6-11 равно
|
|
Окончательно, мы получаем «угловую» функцию альтернативного базиса в виде:
|
|
При таком базисе поузловое распределение равномерной массовой силы не содержит отрицательных нагрузок. Заметим, что уже этих двух базисов достаточно, чтобы с помощью взвешенного усреднения управлять спектром узловых нагрузок.
В заключение мы рассмотрим еще одну из возможных композиций, в которой используется основной квадрат и два треугольника. В треугольнике 1-5-12 гипотенуза изогнута по гиперболе. Относительное приращение текущего уровня при этом определяется так:
|
|
Треугольник 1-6-11 имеет прямолинейную гипотенузу. Такой треугольник использован в предыдущей модели. Теперь «угловая» функция имеет вид:
|
|
Такая модель имеет вполне естественный спектр узловых нагрузок. К тому же кратных нулей здесь вдвое меньше по сравнению с моделью Эргатудиса-Айронса-Зенкевича.
Выводы. Геометрический анализ серендиповых поверхностей дает простой и наглядный способ конструирования базисных функций на элементах высших порядков. Этот подход легко обобщается на трехмерные модели.
New geometrical models of final elements with curvilinear boundaries are constructed.
1. Ergatoudis I., Irons B.M., Zienkiewicz O.C. Curved isoparametric, “quadrilateral” elements for finite element analysis// Int. J. Solids Struct.- Vol.4, 1968. – P.31-42.
2. Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975. – 541с.
3. Митчелл Э., Уэйт Р. Метод конечных элементов для уравнений с частными производными. – М.: Мир, 1981. – 216с.
4. Хомченко А.Н. Некоторые вероятностные аспекты МКЭ/ Ив.-Франк. ин-т нефти и газа. Ивано-Франковск, 1982. – 9с. Деп. в ВИНИТИ 18.03.82, №1213.
5. Хомченко А.Н., Камаева Л.И. О моделировании конечных элементов серендипова семейства// Прикл. проблемы прочности и пластичности: Всесоюзн. межвуз. сб. – Горький: ГГУ, 1985. – С.14-17.
6. Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции// ААЭКС. - №1(19). – Херсон: ХНТУ, 2007. – С.25-30.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.