УДК 519.3:515.2
НОВЫЕ РЕШЕНИЯ ОБОБЩЕННОЙ ЗАДАЧИ БЮФФОНА
Хомченко А.Н.
Посвящается 300-летию со дня рождения Жоржа Бюффона – французского естествоиспытателя
Введение
Знаменитая задача “об игле” (G. Buffon,
1777 г.) представляет исключительный интерес не только для специалистов,
развивающих и применяющих современные технологии рандомизированных вычислений.
Идеи Бюффона стимулировали возникновение и развитие геометрической вероятности,
заложили основы интегральной геометрии, создали теоретический фундамент метода
Монте-Карло. Кроме того, геометрический подход оказался плодотворным для
построения базисных функций конечно-элементной интерполяции. Появились новые
задачи прикладной геометрии и новые приемы геометрического моделирования. Известный
парадокс Бертрана [1], ослабивший на какое-то время доверие к геометрической
вероятности, после убедительных разъяснений Бореля и Пуанкаре стал источником
многочисленных обобщений. Надо отметить, что первое обобщение задачи “об игле”
принадлежит самому Бюффону. К сожалению, Бюффон не нашел правильного решения
обобщенной задачи. Это не удивительно. В математике нет другого такого раздела,
в котором столь же легко допустить ошибку, как в теории вероятностей.
Правильное решение удалось получить Лапласу [2]. Представляет интерес анализ
причин возникновения “ошибочных” решений. “Ошибочными” мы называем решения, не
совпадающие точно с решением Лапласа. “Ошибки” являются результатом некоторой
предвзятости авторов, которая нередко допускается в математическом (в
особенности, стохастическом) моделировании. Понятно, что качество решения
нетрудно установить по экспериментальным оценкам знаменитой константы ![]() .
.
Анализ предшествующих публикаций, постановка задачи
Задача “об игле” Бюффона была сформулирована в 1733 г., а опубликована вместе с решением только в 1777 г. [1, 2]. Появление геометрических вероятностей стало выдающимся событием в науке. Оно способствовало формированию нового языка, стиля и облика теории вероятностей [3]. Благодаря геометрическим вероятностям возникла и бурно развивается интегральная геометрия [4]. Классические результаты Бюффона лежат в основе современного и весьма универсального метода статистического моделирования [5]. В последние годы геометрические вероятности успешно применяются в конечно-элементном анализе [6, 7].
Цель статьи – проиллюстрировать простой и наглядный способ решения классической и обобщенной задачи Бюффона. Особенность предложенного подхода в том, что он обнаруживает одну из причин возникновения “ошибочных” решений обобщенной задачи Бюффона.
Основная часть.
Классическую задачу Бюффона с подробным решением можно найти практически в каждом учебнике или задачнике по теории вероятностей. Обобщенная задача встречается гораздо реже. Например, в [2] можно найти формулировку и ответ Лапласа, а в [8] – формулировку, решение и ответ, не совпадающий с ответом Лапласа. Именно с этими двумя результатами мы будем сопоставлять другие возможные модели.
Сформулируем классическую задачу Бюффона, используя
обозначения [2]. Пусть плоскость разграфлена параллельными прямыми на
расстоянии а друг от друга. На плоскость наугад бросается игла (отрезок)
длины ![]() . Найти вероятность того, что игла
пересечет какую-нибудь из прямых.
. Найти вероятность того, что игла
пересечет какую-нибудь из прямых.
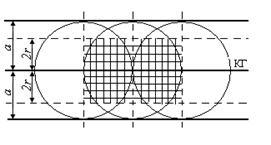
Выберем на рис.1 одну из множества горизонтальных прямых – контрольную горизонталь (КГ).
|
|
|
|
|
Рис.1 К выбору модели |
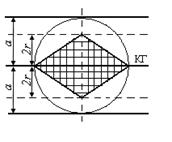
Рис. 2 К вычислению р(А) |
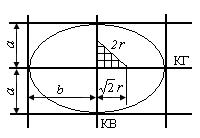
Рис. 3 К вычислению |
Игла бросается на плоскость наугад. Это понимается так, что все пары точек, расстояние между которыми 2r, одинаково возможны. Мы можем (не теряя общности) ограничить пространство Ω элементарных событий кругом радиуса а с центром на КГ. Это естественно, так как по условиям симметрии опыта область Ω должна быть инвариантна относительно параллельного переноса и поворота системы параллельных прямых. Эти круги образуют бесконечную полосу шириной 2а (рис.1). Нас интересует событие А={игла пересекает КГ}. Область “благоприятствования” – полоса шириной 4r (рис. 1). Если исключить наложение соседних кругов, получим модель для геометрического определения искомой вероятности (рис.2) по формуле
|
|
(1) |
где ![]() площадь ромба
(заштрихована);
площадь ромба
(заштрихована); ![]() площадь круга. Заметим, что в
стандартном решении площадь
площадь круга. Заметим, что в
стандартном решении площадь ![]() , как правило,
вычисляется с помощью интегрирования [8]. Предложенная здесь модель в этом
смысле проще. Как и следовало ожидать, она дает тот же результат:
, как правило,
вычисляется с помощью интегрирования [8]. Предложенная здесь модель в этом
смысле проще. Как и следовало ожидать, она дает тот же результат:
|
|
(2) |
Замечание. Условия симметрии опыта позволяют ограничиться лишь одной четвертью области. Именно такую конфигурацию мы используем в обобщенной задаче.
Обобщенную задачу сформулировал
Бюффон, а правильное решение нашел Лаплас (1812 г.). В этом случае плоскость разграфлена двумя системами параллельных прямых: горизонталями с
интервалом а и вертикалями с интервалом b. На плоскость наугад бросается
игла длины ![]() . Найти вероятность того, что игла
пересечет хотя бы одну из прямых.
. Найти вероятность того, что игла
пересечет хотя бы одну из прямых.
Теперь плоскость покрыта ортогональной сеткой с
прямоугольными ячейками. Понятно, что неравномерная дискретизация (![]() ) деформирует круг Ω в эллипс.
Обычно с помощью такой сетки моделируют физическую ортотропию среды, а
эллиптическое диффузионное пятно можно наблюдать в лабораторных экспериментах.
В центре эллипса пересекаются контрольная горизонталь (КГ) и контрольная
вертикаль (КВ). Кроме события А в рассмотрение вводится случайное
событие В={игла пересекает КВ}. Поскольку А и В
совместны, вычислительная формула имеет вид:
) деформирует круг Ω в эллипс.
Обычно с помощью такой сетки моделируют физическую ортотропию среды, а
эллиптическое диффузионное пятно можно наблюдать в лабораторных экспериментах.
В центре эллипса пересекаются контрольная горизонталь (КГ) и контрольная
вертикаль (КВ). Кроме события А в рассмотрение вводится случайное
событие В={игла пересекает КВ}. Поскольку А и В
совместны, вычислительная формула имеет вид:
|
|
(3) |
При вычислении р(А) используется прямоугольный треугольник с катетами 2r и b. При вычислении р(В) используется треугольник с катетами 2r и а. А вот при вычислении p(AB) применяются различные, иногда недостаточно обоснованные, гипотезы [3]. Главный вопрос: являются ли события А и В независимыми? Опубликованные решения свидетельствуют о том, что здесь единого мнения нет. По нашему мнению, лучше пользоваться геометрической вероятностью, подбирая подходящие размеры и форму области АВ. Например, на рис. 3 показана область “благоприятствования” событию АВ. Именно при таком выборе мы получаем известное решение Лапласа [2]:
|
|
(4) |
Стоит обратить внимание на то, что в модели Лапласа ![]() , что означает зависимость случайных
событий А и В. При решении этой же задачи авторы [8] опираются
на независимость А и В. Возможно, поэтому их ответ
, что означает зависимость случайных
событий А и В. При решении этой же задачи авторы [8] опираются
на независимость А и В. Возможно, поэтому их ответ
|
|
(5) |
не совпадает с ответом Лапласа. Кстати, в формуле (5) нелегко усмотреть геометрическое содержание.
Если аппроксимировать область АВ астроидой с
вершинами на контрольных прямых в точках ![]() ,
то можно получить новое решение обобщенной задачи Бюффона:
,
то можно получить новое решение обобщенной задачи Бюффона:
|
|
(6) |
Тестирование нелапласовых решений показывает, что
формула (6) “ближе” к решению Лапласа. Решение с астроидой можно существенно
улучшить, если вершины астроиды выбрать в точках ![]() .
Незначительное сжатие астроиды дает более реалистичную область АВ.
.
Незначительное сжатие астроиды дает более реалистичную область АВ.
Фактически в решении Лапласа использована идея детерминизации математической модели путем замены случайной величины её математическим ожиданием. Это излюбленный прием статистической физики. Случайной величиной является ширина полосы, образованной иглами, пересекающими контрольную прямую. Легко заметить, что средняя ширина полосы (математическое ожидание) равна 2r. Поэтому область “благоприятствования” для АВ – квадрат со стороной 2r.
Выводы
Обобщенная задача Бюффона – весьма интересный объект
для компьютерных экспериментов. Эмпирические оценки числа ![]() дают представления о качестве той или
иной аппроксимации.
дают представления о качестве той или
иной аппроксимации.
Three different solutions of generalized Buffon problems are analyzed.
- Секей Г. Парадоксы в теории вероятностей и математической статистике. – М.: Мир, 1990. – 240 с.
2. Математическая энциклопедия. – М.: Советская энциклопедия. Т.1. А-Г. 1977. – С.571-572.
- Кендалл М., Моран П. Геометрические вероятности. – М.: Наука, 1972. – 192 с.
4. Сантало Л. Интегральная геометрия и геометрические вероятности. – М.: Наука, 1983. – 360 с.
- Ермаков С.М., Михайлов Г.А. Статистическое моделирование. – М.: Наука, 1982. – 296 с.
6. Хомченко А.Н. Метод конечных элементов: стохастический подход / Ив.-Франк. ин-т нефти и газа. – Ивано-Франковск, 1982. – 7 с. Деп. В ВИНИТИ 15.10.82, №5167.
- Хомченко А.Н. Вероятностные схемы в дискретном анализе температурных полей // Инж.-физич. журнал. – 1988. Т.55, №2. – С.323-324.
8. Вентцель Е.С., Овчаров Л.А. Прикладные задачи теории вероятностей. – М.: Радио и связь, 1983. – 416 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.