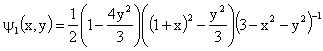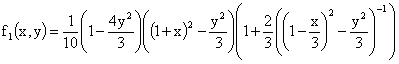УДК 517.2
БАРИЦЕНТРИЧЕСКИЕ ОЦЕНКИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В КРУГЕ
Хомченко А.Н., Цыбуленко О.В., Дембровская М.В.
Постановка проблемы
Основная проблема теории эллиптических задач заключается в разработке простых, удобных и достаточно точных методов быстрой оценки стационарного поля, сформированного граничными потенциалами. Рассматриваемые здесь методы исследования электростатических полей без каких-либо усложнений распространяются на гидромеханику безвихревых течений идеальной жидкости, стационарные температурные поля, некоторые задачи плоской теории упругости и другие задачи, опирающиеся на модель „мыльной пленки” [1]. Повышенное внимание исследователей к круглой области мотивируется следующими причинами. Во-первых, круговая область имеет самостоятельное значение, и для нее получены точные решения многих важных задач. Во-вторых, экспериментаторы часто используют круг в своих опытах. Это позволяет оценивать возможности новых методов с помощью тестов на круге. Наконец, еще одна, не менее важная причина заключается в том, что многие области произвольного очертания допускают конформное отображение в круг. Очень важно, что при конформном отображении уравнение Лапласа ![]() , моделирующее потенциал электростатического поля в координатной плоскости
, моделирующее потенциал электростатического поля в координатной плоскости ![]() , переходит снова в уравнение Лапласа
, переходит снова в уравнение Лапласа ![]() в координатной плоскости
в координатной плоскости ![]() . Далеко не все уравнения в частных производных обладают этим важным свойством инвариантности. Для исследования электростатического потенциала в плоской области мы применяем методы барицентрического усреднения (МБУ), опирающиеся на полезные свойства центра масс (барицентра) материальных точек (расчетных узлов на границе области).
. Далеко не все уравнения в частных производных обладают этим важным свойством инвариантности. Для исследования электростатического потенциала в плоской области мы применяем методы барицентрического усреднения (МБУ), опирающиеся на полезные свойства центра масс (барицентра) материальных точек (расчетных узлов на границе области).
Анализ предшествующих публикаций
МБУ появились как результат настойчивых попыток одного из авторов настоящей статьи разработать упрощенный несеточный метод типа Монте-Карло для решения уравнения Лапласа с граничными условиями Дирихле [2-4].
Наибольшее распространение получил вариант МБУ с треугольным вычислительным шаблоном (симплексом) и барицентрическими координатами исследуемой точки в качестве весов монте-карловской оценки. В предшествующих работах показано, что на таком шаблоне реализуется схема случайных блужданий частицы в симплексе с поглощающими узлами в вершинах. Именно такая схема отвечает граничным условиям Дирихле. Симплекс-шаблон легко адаптируется к границам произвольной конфигурации, поэтому в таком варианте МБУ можно обойтись без конформного отображения области в круг. Любое фиксированное положение симплекса („стоп-кадр”) ассоциируется с выборкой из трех граничных значений потенциала. Совокупность „стоп-кадров” дает выборку граничных значений потенциала, „расслоенную” по три значения в группе. Некоторые граничные значения могут входить в разные группы. На каждом „стоп-кадре” трехточечная граничная задача решается точно. Это означает, что потенциал, построенный на симплекс-шаблоне, точно удовлетворяет уравнению Лапласа, а также граничным условиям Дирихле. Заключительный этап сводится к вычислению арифметического или взвешенного среднего на совокупности „стоп-кадров”. Если же область круговая, то в качестве вычислительного шаблона можно использовать правильный шестиугольник, вписанный в окружность. Теперь моделируется шестимаршрутная схема блужданий, и этого часто бывает достаточно для получения приемлемой точности вычислений. В отличие от МБУ с треугольным шаблоном в этом варианте можно ограничиться всего одним „стоп-кадром”. В качестве весов в монте-карловских оценках используются гексагональные базисы: ПБ (полиномиальный) [5, 6] или ДРБ (дробно-рациональный) [7, 8]. Представляет интерес сравнение альтернативных базисов с точки зрения точности вычислений электростатического потенциала в круге. С этой целью ниже сформулирована задача Дирихле для уравнения Лапласа в круге, допускающая построение точного решения.
Постановка задачи
Сечение бесконечной металлической трубы – круг единичного радиуса. На границе сечения задан потенциал: ![]() , где
, где ![]() и
и ![]() ‑ экстремальные значения потенциала. Найти распределение электростатического потенциала внутри трубы. Математическая формулировка задачи такова: внутри круга
‑ экстремальные значения потенциала. Найти распределение электростатического потенциала внутри трубы. Математическая формулировка задачи такова: внутри круга ![]() найти решение уравнения Лапласа:
найти решение уравнения Лапласа:
|
|
(1) |
удовлетворяющее граничному условию
|
|
(2) |
где ![]() – полярные координаты текущей точки.
– полярные координаты текущей точки.
Основная часть
В математической физике уравнение (1) часто называют уравнением потенциала. Это связано с тем, что этому же уравнению удовлетворяет потенциал магнитного поля в магнитостатике, а также потенциал гравитационного поля в теории гравитации Ньютона. Уравнение (1) является математической моделью и для множества других физических явление [1]. Легко убедиться, что решением задачи (1)-(2) является функция [9]:
|
|
(3) |
В прямоугольных декартовых координатах решение имеет вид:
|
|
(4) |
а граничное условие:
|
|
(5) |
В численных экспериментах экстремальные значения потенциала будут конкретизированы.
Как видим, заданное граничное условие сформировало достаточно сложное электростатическое поле в виде седлообразной поверхности гиперболического параболоида (гипара). Гауссова кривизна гипара отрицательна. Во многих задачах с этим свойством связаны дополнительные трудности.
Предварительный (докомпьютерный) анализ решения показывает, что арифметическое среднее экстремальных граничных значений потенциала установилось не только в центре круга (что вполне естественно), но и на взаимно перпендикулярных диаметрах, совпадающих с биссектрисами координатных углов. Это линии среднеарифметического уровня, которые отделяют выпуклые участки поверхности ![]() от вогнутых. Четко выраженная симметрия точного решения есть результат „суперпозиции” симметрии граничного условия и симметрии исследуемой области. Это позволяет при детальном исследовании поля ограничиться лишь четвертью круга. Вполне понятно, что такую выпукло-вогнутую поверхность сложно аппроксимировать линейными полиномами на треугольных носителях – симплексах. Для получения приемлемой точности потребуются не только предварительные знания о поведении граничной функции, но и опыт компьютерных экспериментов с МБУ. Основные трудности связаны с неудачным выбором расчетных узлов и неправильной оценкой необходимого количества „стоп-кадров”. Таким образом, выборки граничных значений могут быть (по терминологии математической статистики) нерепрезентативными, что приводит к искажениям выборочного среднего (барицентрической оценки). На рис. 1 изображены линии уровня электростатического поля в круге единичного радиуса при
от вогнутых. Четко выраженная симметрия точного решения есть результат „суперпозиции” симметрии граничного условия и симметрии исследуемой области. Это позволяет при детальном исследовании поля ограничиться лишь четвертью круга. Вполне понятно, что такую выпукло-вогнутую поверхность сложно аппроксимировать линейными полиномами на треугольных носителях – симплексах. Для получения приемлемой точности потребуются не только предварительные знания о поведении граничной функции, но и опыт компьютерных экспериментов с МБУ. Основные трудности связаны с неудачным выбором расчетных узлов и неправильной оценкой необходимого количества „стоп-кадров”. Таким образом, выборки граничных значений могут быть (по терминологии математической статистики) нерепрезентативными, что приводит к искажениям выборочного среднего (барицентрической оценки). На рис. 1 изображены линии уровня электростатического поля в круге единичного радиуса при ![]() .
.
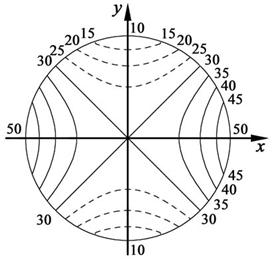
Рис. 1 Линии уровня электростатического поля в круге.
На выпуклых участках сплошные линии, на вогнутых – пунктирные.
Линии уровня поля представляют собой гиперболы с асимптотами, параллельными биссектрисам координатных углов. Фрагмент поверхности гиперболического параболоида, вырезанный по асимптотам (с прямоугольным планом), широко применяется в строительстве. Специалисты называют такую оболочку асимгиполоидом.
Адекватное моделирование нелинейных эффектов распределения потенциала достигается применением более совершенных вычислительных шаблонов МБУ (например, гексагональных). Ясно, что веса монте-карловских оценок и в этом варианте МБУ определяются так, чтобы исследуемая точка внутри области служила центром масс (барицентром) расчетных узлов на границе области. Первые вычисления на гексагональных дискретных элементах были связаны с исследованиями нейтронной диффузии и теплопроводности в ядерных реакторах. Существенных результатов в этом направлении достиг Ишигуро, который в начале 80-х годов прошлого века на основе идей Уачспресса сконструировал ДРБ [7]. К этому же времени удалось построить и ПБ на правильном шестиугольнике [5, 6]. Здесь мы используем эти базисы в качестве весовых коэффициентов монте-карловских оценок электростатических потенциалов в круге. Вычислительная технология заключается в следующем. Первую вершину (расчетный узел) вписанного в круг гексагона совмещаем с точкой (1;0). Остальные расчетные узлы располагаются на контуре круга регулярно через 600. Для первого угла запишем выражения функции формы:
|
ДРБ 1: |
|
(6) |
|
ДРБ 2: |
|
(7) |
|
ПБ: |
|
(8) |
Остальные функции базисов получаются соответственно из (6)-(8) последовательным поворотом системы координат на 600. Нетрудно убедиться, что все базисы удовлетворяют интерполяционной гипотезе Лагранжа. Это означает, что базисная функция, отвечающая узлу k равна единице в этом узле и нулю – в остальных узлах гексагона. Оценка электростатического потенциала в произвольной внутренней точке ![]() круга имеет вид математического ожидания. Например, для ПБ:
круга имеет вид математического ожидания. Например, для ПБ:
|
|
(9) |
где ![]() ‑ значение граничного потенциала в узле k.
‑ значение граничного потенциала в узле k.
В таблице сопоставлены точные значения, линейная (на треугольнике), билинейная (на квадрате) и гексагональная аппроксимации (ПБ и ДРБ) потенциалов в круге.
Таблица 1
Точные значения и барицентрическая аппроксимация потенциалов.
|
точка |
точный потенциал |
линейная аппрокс. |
билинейн. аппрокс. |
гексагон ДРБ-1 |
гексагон ДРБ-2 |
гексагон ПБ |
|
|
30 |
30
|
30
|
30
|
30
|
30
|
|
|
35 |
34,35
|
35
|
33,33
|
34,33
|
35
|
|
|
23,75 |
23,71
|
23,75
|
23,64
|
24,16
|
23,75
|
Примечание: Буквой ![]() обозначена относительная погрешность.
обозначена относительная погрешность.
Выводы и перспективы
Рассмотренная задача – убедительная иллюстрация к известному утверждению о том, что граничное условие „сильнее” дифференциального уравнения. В самом деле, отчетливо выраженное немонотонное поведение поля обусловлено граничной функцией (2). Не всякий вычислительный шаблон способен с достаточной точностью восстановить такое поле, в особенности, если величина размаха экстремальных значений граничных потенциалов на порядок (и более) превосходит диаметр исследуемой области. Линейная и билинейная аппроксимации имеют повышенную чувствительность к изменению положения вычислительного шаблона, что требует увеличения количества „стоп-кадров”. Можно получить безошибочные результаты на единственном „стоп-кадре” билинейной аппроксимации, если вершины квадрата совместить с точками экстремальных граничных потенциалов. Именно эти результаты помещены в таблицу. Среди гексагональных шаблонов выгодно отличается модель с ПБ, которая обеспечивает безошибочные вычисления независимо от ориентации „стоп-кадров”. В перспективе планируется пополнение барицентрического „инструментария” вычислительным шаблоном с ортогональными маршрутами. Такой шаблон, как и симплекс, хорошо адаптируется к границам произвольной конфигурации. Кроме того, интересно учесть влияние заземлений на отдельных участках границы исследуемой области.
|
The noncomplicated algorithms of barycentrical averaging method for estimation of electrostatic field in the circle are proposed. The obtained approximations are compared with the exact solution. |
1. Фарлоу С. Уравнения с частными производными для научных работников и инженеров: Пер. с англ. – М.: Мир, 1985.– 384 с.
2. Хомченко А.Н., Иванов В.А., Камаева Л.И., Петрина В.Н. Расчет футеровки шахтных копровых шкивов // Изв. вузов. Горный журнал. – 1986. № 5. – С. 69–71.
3. Хомченко А.Н. Случайные блуждания и конечноэлементные аппроксимации температурных полей // Матем. модели, методы решения и оптимальн. проектир. гибких пластин и оболочек: Межвуз. сб. научн. тр. – Саратов: СГУ, 1988.– С. 80–82.
4. Хомченко А.Н. Вероятностные схемы в дискретном анализе температурных полей // Инж. – физич. журнал. 1988. – Т. 55, № 2. – С. 323–324.
5. Хомченко А.Н. Об одном проекционно-сеточном алгоритме вычислительной механики // VI Всесоюз. съезд по теор. и прикл. механике: Аннот. докл. – Ташкент, 1986. – С.628–629.
6. Хомченко А.Н. К расчету температурных полей в сотовых структурах методом конечных элементов // Инж. – физич. журнал. 1987. – Т. 52, № 2. – С. 301–305.
7. Ishiguro M. Construction of hexagonal basis functions applied in the Galerkin–type finite element method. // J. Inf. Process. 1984. V.7, №2. – P. 89–95.
8. Хомченко А.Н. О дробно – рациональной интерполяции на шестиугольном конечном элементе // Вісник Запорізького державного університету (Серія: фізико–математичні науки). – 2002. – № 3. – С. 84–87.
9. Будникова Т.В., Жукова-Малицкая Г.А., Кузьмин Ю.Н. Задачи по математической физике. – Ленинград: ЛПИ, 1981. –86 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.