Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 004.043:004.89

МЕТОДЫ ХРАНЕНИЯ И ОБРАБОТКИ НЕЧЕТКИХ ДАННЫХ В СРЕДЕ РЕЛЯЦИОННЫХ СИСТЕМ

Касаткина Н.В., Танянский С.С., Филатов В.А.

Введение

Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) продолжают привлекать внимание исследователей в области интеллектуальных, экспертных систем, а также систем поддержки принятия решений. Эти понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh). Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять несколько периодов. Первый период (конец 60-х – начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л.Заде, Э.Мамдани). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами. Одновременно внимание уделялось разработке экспертных систем, построенных на нечеткой логике, и нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в сфере финансов, анализа и принятия управленческих решений и многих других.

В последнее десятилетие отмечается гибридизация методов интеллектуальной обработки информации.  Мягкие вычисления объединяют такие области как нечеткая логика, искусственные нейронные сети, извлечение знаний, базы данных, вероятностные рассуждения, эволюционные алгоритмы и ряд других. Они дополняют друг друга и используются в различных комбинациях для создания гибридных интеллектуальных систем.

Не остались в стороне от интересного и современного направления исследователи в области баз данных. Разрабатывается нечеткая реляционная алгебра и специальные расширения структурированного языка (SQL) для нечетких запросов. В этой области интенсивные исследования проводят европейские ученые Д.Дюбуа и Г.Праде. Формируется перспективное направление в современных системах обработки информации – нечеткие запросы к базам данных (fuzzy queries).

В этом контексте можно рассматривать два основных вопроса, наиболее актуальных в настоящее время: (1) как проектировать, (2) где и в каких структурах хранить нечеткие данные систем такого класса.

Решение этих проблем откроет пути интеграции накопивших колоссальные объемы информации реляционных баз данных и систем на основе нечеткой логики.

Целью проводимых исследований является разработка методов хранения и обработки нечетких данных средствами реляционной модели, ориентированной на реализацию в среде современных систем управления базами данных (СУБД). Особое внимание уделено обоснованию выбора схемы реляционной модели данных для представления функций принадлежности лингвистических переменных.

Основные свойства реляционной модели

Рассмотрим классический подход к построению реляционного отношения, предложенный Э.Коддом [1], и выделим основные свойства отношений при расширении множества доменов.

Основной структурной компонентой данных в реляционной модели данных (РМД) является n-арное отношение, представляющее собой подмножество кортежей декартова произведения доменов, то есть множества значений элементов данных. Для заданных конечных множеств D₁,…, D_n (не обязательно различных по типу) декартовым произведением D₁´…´ D_n называется множество произведений вида d₁,…, d_n, где d₁ÎD₁,…, d_nÎD_n.

Отношением R, определенным на множествах D₁,…, D_n, называется подмножество произведения (декартово произведение) D₁´…´ D_n, то есть R Í D₁´D₂´…´D_n.

Множество D = {D₁,…, D_n} называется доменом. Домены – это однотипные семантически однозначные (одинаковые по смыслу) значения элементов данных. Элементы декартова произведения d₁,…, d_n называются кортежами, число n определяет степень отношения; количество кортежей определяет мощность отношения.

Пусть a = {a₁,…, a_n} – множество имен,  тогда  введем  однозначное отображение вида r : a_i ® D_i , где пару A_i = < r (a_i),  D_i > называют атрибутами отношения.

Схемой отношения R будем называть выражение S (A₁,…, A_n) в котором все атрибуты A_i различны. При этом экземпляр отношения R(S) определяется как подмножество декартова произведения доменов  r_i Í r(a_i) ´…´ r(a_n). Экземпляр отношения со схемой R_i будем обозначать как R_i (r_i). Отметим, что перестановка атрибутов в схеме не порождает нового состояния БД. Таким образом, множество атрибутов {A₁,…, A_n} задает тип отношения и определяет его свойства.

Схему БД будем обозначать как множество схем отношений U = {R₁,…, R_n}, где R_i Î R и все R_i различны. Соответственно, экземпляр БД будем обозначать множеством экземпляров отношений U (r₁,…,r_n).

Концептуально реляционная БД является информационной моделью предметной области (ПО), такой, что каждый экземпляр соответствует некоторому состоянию ПО в определенный момент времени. Каждое состояние моделируется упорядоченной совокупностью значений элементов данных, соответствующих значениям свойств объектов ПО. Объекту определенного типа соответствует кортеж отношения [2].

Структура фаззифицированного отношения

Для задач анализа данных определим дополнительный тип отношений, определяющий принадлежность существующих данных к некоторому заданному числовому отрезку, определяющему характеристику рассматриваемого информационного объекта.

Любую линию на координатной плоскости можно представить в виде бинарного отношения, где Dom R описывается значениями оси абсцисс, а Im R описывается значениями оси ординат. В задаче фаззификации диаграмма содержит три показателя, которые необходимо учитывать при формировании отношения.

Будем понимать под нечеткой переменной набор (N, X, Y), где N – это название переменной, X – область рассуждений, Y – нечеткое множество на X. Используя такое определение, зададим три домена, соответствующих элементам переменной [3].

Пусть N = {n₁,…, n_m}, Y = {0, 0.1,…, 1}, X = {x₀,…, x_k}. Значения X и Y соответствуют выбранной шкале дискретизации координатных осей и описывают область принадлежности к параметру N. Для каждого параметра N делаем выборку данных по значениям X и строим диаграмму принадлежности, имеющую вид, представленный на рис. 1.

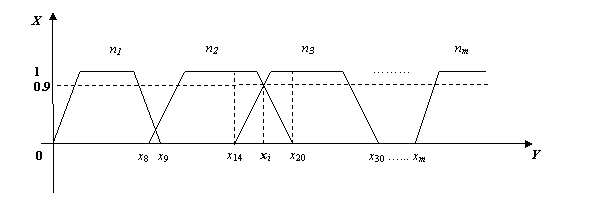
Рис. 1 Распределение количества защит диссертаций по регионам

Для рассмотренного случая определим соответствующие домены для представления нечеткой переменной.

D₁ = {n₁, n₂, n₃,…, n_m};

D₂ = {x₀,…, x₈, x₉,…, x₁₄,…, x_i,…, x₂₀,…, x₃₀,…, x_m};

D₃ = {0, 0.1,…, 1}.

Зададим множество имен доменов и построим отображение. Для множества имен A = {A₁, A₂, A₃} отображение r : (A₁ ® D₁; A₂ ® D₂; A₃ ® D₃) определит множество атрибутов A = {A₁, A₂, A₃} и соответствующую схему отношения S(A₁, A₂, A₃).

Возможные пересечения диаграмм фаззификации определяют тот факт, что все значения могут повторяться относительно друг друга. Например, рассмотрим фрагмент отношения для показателей {x₁₄, x_i, x₂₀} представленный на рис. 2.

Рис. 2 - Фрагмент данных для выбранных показателей.

Таким образом, можно говорить об отношении, включающем полный набор кортежей декартова произведения доменов D₁´D₂´D₃ (полное декартово произведение, в данном случае, определяется конечностью значений системы координат). Исходя из этого факта, можно заключить, что ключом отношения будет множество всех атрибутов K = {A₁, A₂, A₃}.

Очевидно, что информативность кортежей определяется значениями на диаграмме фаззификации. Исходя из рассматриваемой задачи, необходимо учитывать еще один показатель – множество значений выборки из БД,  для которой строится диаграмма. То есть необходимо установить связь между доменом отношения R ^f, отражающим значения оси абсцисс и доменом из БД, содержащим значения параметров фаззификации.

Таким образом, следующая задача, которую необходимо рассмотреть, связана с интеграцией отношения R ^f с БД, хранящей основные показатели.

Обработка параметров фаззификации

Рассмотрим задачу в общем виде. Пусть U (R₁,…, R_n) – БД, хранящая основные данные, R ^f(A₁, A₂, A₃) – отношение фаззификации. Задача будет иметь смысл, если в БД U существует параметр, относительно которого выполнена фаззификация.

Чтобы организовать совместную работу с базами данных U и R, формализуем процедуру интеграции, опираясь на поэтапную нормализацию. Структура БД U получена на основании функциональных зависимостей F = {M_i ® N_i} где M_i, N_i Î U. Выделим одну зависимость, которая включает атрибут с параметрами фаззификации, и обозначим ее как W ® V, причем W и V могут быть множествами. Отношение R ^f содержит одну зависимость вида F¢ = {A₁, A₂, A₃ ® A₁, A₂, A₃}. Опираясь на аксиомы вывода, можно получить эквивалентное множество F¢ = {A₁, A₂, A₃ ® A₁; A₁, A₂, A₃ ® A₂; A₁, A₂, A₃ ® A₃}.

Пусть параметр фаззификации соответствует атрибуту A₂, тогда для определения типа связи необходимо получить множество F = F È F¢ и рассмотреть два случая, влияющих на правила нормализации.

1.                  A₂ Î W – поиск неполных зависимостей: если выполняются функциональные зависимости x ® z и w ® z, причем w Í x, тогда зависимость w ® z является неполной.

2.                  A₂ Î V – поиск транзитивно зависимых элементов: если выполняются функциональные зависимости x ® w и w ® z, тогда элемент z является транзитивно зависимым.

Существование таких зависимостей позволит выполнить корректную декомпозицию и установить связь между базой данных U и R ^f.

Если A₂ = W или A₂ = V, то процесс декомпозиции приводит ко второй или третьей нормальной форме. Если равенства не выполняются, то организовать поддержку однозначности связных данных нельзя, так как ассоциация между отношениями будет соответствовать типу «многие-ко-многим».

Как правило, на практике условия равенства не выполняются и для нормализации необходимо выделить базис F и повторить процедуру декомпозиции. Учитывая тот факт, что структура БД не должна изменяться, необходимо связать отношение фаззификации R ^f и БД U без реструктуризации схемы данных. Используя диаграмму модели «сущность-связь», представим R ^f и U в виде сущностей (рис. 3).

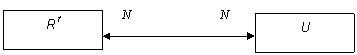Рис. 3 Диаграмма «сущность-связь» между БД U и R ^f

Для устранения связи “N:N” введем дополнительную связующую сущность, которая решит проблему целостности данных за счет определения новых типов связей. Такая сущность будет содержать один атрибут – связующий для R ^f и U, причем по объективным причинам он будет ключевым. На рис. 4 показана диаграмма интеграции БД и отношения фаззификации с поддержкой однозначности связи.

Рис. 4 Устранение связи «многие-ко-многим»

Исходя из описания концептуальной схемы ПО видно, что для корректного соединения R ^f и U необходимо построить промежуточную таблицу. Такой подход гарантирует согласованность данных для любых типов параметров фаззификации.

Покажем, что для рассматриваемой задачи вполне корректны результаты при выполнении соединения отношений с ассоциацией типа “N:N”. Возможные значения атрибута A₁ Î U могут повторяться столько раз, сколько данное значение пересекает границы диаграммы фаззификации по оси ординат (см. рис. 1). То есть каждому значению атрибута A₁ соответствует строка уникальных  данных. Если A₁ не является ключом, и значения повторяются, то, по определению множества, в строке должно быть хотя бы одно отличное значение. В терминах решаемой задачи необходимо анализировать все такие строки. В атрибуте A₁ отношения R ^f также повторяются значения, которые необходимо проанализировать, причем во всевозможных комбинациях.

Таким образом, в общем виде для анализа данных, накапливаемых в реляционных  базах данных, достаточно построить фаззифицированное отношение и установить связь с атрибутом (атрибутами), по значениям которого необходимо провести соответствующий анализ.

Пример

Для иллюстрации разработанного подхода рассмотрим пример построения интегрированной информационной системы, объединяющей в себе реляционную базу данных и подсистему на основе нечеткой логики.

В 1999 году для Высшей аттестационной комиссии Украины (ВАК Украины) была разработана информационная система обработки, хранения и анализа учетных карточек соискателей на присуждение ученых степеней кандидата или доктора наук. Схема реляционной базы данных включает ряд атрибутов, в том числе:

-                   фамилия, имя, отчество соискателя,

-                   дата рождения,

-                   область наук,

-                   специализированный совет, где проводилась защита диссертации,

-                   город, где расположен специализированный совет,

-                   дата защиты диссертации и ряд других атрибутов.

За время эксплуатации информационная система «ВАК Украины» показала свою эффективность и надежность. В настоящее время база данных насчитывает около 45000 записей. Каждый кортеж в базе данных - это сведения о соискателе, его диссертационной работе, месте и времени защиты. Таким образом, база данных содержит скрытые знания о данной предметной области. Применив технологию запросов к базе данных с использованием стандартных операций – группировки (GROUP), подсчета количества записей (COUNT), подсчета суммы (SUMM), определения максимального  (MAX) и минимального значения (MIN) можно определить некоторые закономерности предметной области, относящиеся к категории скрытых знаний [4].

Количество соискателей, претендующих на ученую степень кандидата технических наук с 1999 по 2008 год, представлено на рис. 5.

Использование технологии запросов с применением функции фильтрации позволяют пользователю получать разнообразные статистические данные, аналогичные рассмотренному выше примеру.

Исследования в области мягких вычислений и технология представления функций принадлежности лингвистических переменных средствами реляционной модели, подробно рассмотренные в данной статье, позволяют проводить анализ данных в разрезе нечетких запросов типа «БОЛЬШЕ», «МЕНЬШЕ», «СТАРЫЙ», «МОЛОДОЙ» и т.д.

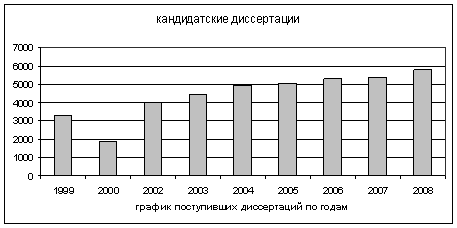
Рис. 5 Поступление  в ВАК кандидатских диссертаций по годам

Рассмотрим пример формирования и реализации средствами реляционной СУБД подсистемы нечеткого анализа в терминах «МОЛОДОЙ», «ЗРЕЛЫЙ» и «СТАРЫЙ» кандидат технических наук. Возраст будем определять на дату защиты диссертации. Этот атрибут «Возраст Защиты» может быть легко получен в результате вычитания и простого преобразования двух дат из базы данных «ВАК Украины»: «Дата рождения» и «Дата защиты».

Функции принадлежности лингвистической переменной «ВОЗРАСТ» будут иметь вид, представленный на рис. 6.

Для хранения всех данных лингвистической переменной «ВОЗРАСТ» проектируется отношение с тремя атрибутами: «Годы», «Имя Переменной», «Значение функции принадлежности». Все атрибуты будут объединены в тройной составной ключ. Атрибут «Имя Переменной» предназначен для хранения повторяющихся групп лингвистической переменной «ВОЗРАСТ» - {«МОЛОДОЙ», «ЗРЕЛЫЙ», «СТАРЫЙ»}, поэтому для хранения уникальных значений проектируется отдельное отношение – «Справочник подмножеств» (С_Подмножеств). Следующим этапом построения общей схемы базы данных необходимо создать связь между атрибутами «Возраст Защиты» отношения «Соискатели» базы данных «ВАК Украины» и атрибутом «Годы» отношения «Возраст»  Схема интегрированной базы данных приведена на рис. 7.

Модифицированная реляционная модель данных, рассмотренной информационно-аналитической системы, позволяет выполнять нечеткие запросы в терминах  «МОЛОДОЙ», «ЗРЕЛЫЙ», «СТАРЫЙ» кандидат наук в сочетании с детерминированными четкими значениями базы данных.  Например: определить при помощи запроса, с каким значением функции принадлежности по переменным «МОЛОДОЙ», «ЗРЕЛЫЙ», «СТАРЫЙ» защищаются соискатели в области научных исследований – технические науки. Результат выполнения запроса представлен на рис. 8.

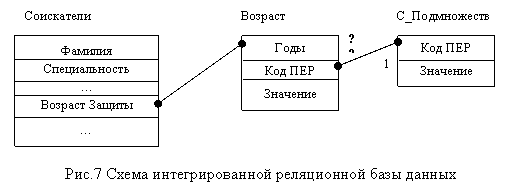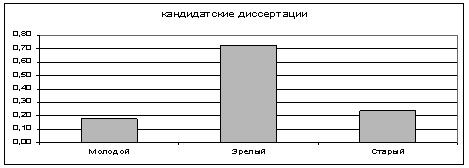
Рис.8 Распределение по категориям «МОЛОДОЙ», «ЗРЕЛЫЙ», «СТАРЫЙ»

Выводы

Статья посвящена исследованию методов и структур хранения и обработки нечетких данных средствами реляционного представления и моделирования с ориентацией на реализацию в среде современных СУБД. Особое внимание уделено обоснованию выбора схемы реляционной модели данных для представления функций принадлежности лингвистических переменных. Реляционная модель представления и реализации нечетких моделей может стать связующим звеном для интеграции с существующими реляционными базами данных. Это позволит получить новый инструмент для извлечения новых ранее недоступных данных и знаний. Приведен пример, подтверждающий эффективность разработанного подхода.

ЛИТЕРАТУРА

1.                  Мейер Д. Теория реляционных баз данных: Пер. с англ. – М.: Мир, 1987. – 608 с.

2.                  Конноли Т., Бегг К. Базы данных: проектирование, реализация и сопровождение. Теория и практика, 2-е изд.: Пер с англ. - М.: «Вильямс», 2000. - 1120 с.

3.                  Гибридные нейро-фаззи модели и мультиагентные технологии в сложных системах: монография / В.А. Филатов, Е.В. Бодянский, В.Е. Кучеренко и др. ; под общ. ред. Е.В. Бодянского. – Дніпропетровськ: Системні технології, 2008. – 403 с.

4.                  Касаткина, Н.В. Об одном подходе к интеллектуальному анализу реляционных баз данных / В.А. Филатов, Н.В. Касаткина // Вестник Херсонского национального технического университета № 1 (34) – 2009. –  С. 157-161.