УДК 681.518.52:544.023.523 002.56
Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Кириллов О.Л. , Якимчук Г.С.
Введение
После отработки технологий получения из нефти продуктов методом крекинг - перегонки столкнулся с проблемой доставки этих продуктов, складирования и распределения. Ряд неудач в вопросах перегрузки по емкостям определил проблему управления этим процессом. Исследования выявили, что характер этого физического процесса напрямую зависит от поведения генерируемого зарядами электростатического поля (ЭСП), а разрешение проблемы следует искать в изучении параметров этого поля и влиянии внешних факторов на его поведение. Результат работ в этом направлении позволил получить безопасные программы перегрузки, однако они не удовлетворяют экономическим и временным требованиям развития современных технологий.
В сложившемся противоречии скорости и безопасности транспортирования нефтепродуктов развитие вопроса оптимизации технологии систем перегрузки становиться актуальным и требует современного решения в условиях глобального кризиса. Разрешение совокупности этого вопроса и других позволит ускорить выход страны на более высокий уровень развития.
Постановка задачи
Смоделировать процесс функционирования и исследовать адаптивную систему автоматического управления перегрузкой углеводородных жидких топлив (УЖТ) в технологическую емкость (ТЕ) при условии электростатической безопасности (ЭСБ).
Решение задачи
Предлагаемая адаптивная система предназначена для управления уровнем расхода при заполнении ТЕ нефтепродуктами по интегральному параметру, потенциалу![]() . Сложность задачи перегрузки заключена в этой емкости, которая накапливает заряд при подаче СПЖ. В результате перегрузки возникают проблемы ЭСБ и гидродинамики процесса заполнения. Для решения этих и других проблем в качестве двигателя взят ассинхронный двигатель (АД), управляемый от преобразователя частоты, а при регулировании подачи используется насос, а не задвижки. Подача осуществляется снизу емкости, что позволяет осуществить плавное окончание процесса при достижении равенства давлений в нагнетаемом трубопроводе и энергии встречного уровня жидкости [1].
. Сложность задачи перегрузки заключена в этой емкости, которая накапливает заряд при подаче СПЖ. В результате перегрузки возникают проблемы ЭСБ и гидродинамики процесса заполнения. Для решения этих и других проблем в качестве двигателя взят ассинхронный двигатель (АД), управляемый от преобразователя частоты, а при регулировании подачи используется насос, а не задвижки. Подача осуществляется снизу емкости, что позволяет осуществить плавное окончание процесса при достижении равенства давлений в нагнетаемом трубопроводе и энергии встречного уровня жидкости [1].
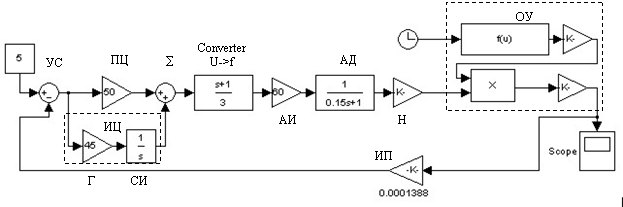
Рис.1. Структурная схема управления насосом АМ
При построении и моделировании процесса управления насосом системы перегрузки (рис.1) возникли проблемы определения конфигурации, отыскания способа замкнутости системы через регулятор, выбор регулятора, представление двигателя и насоса в общей схеме, объекта управления (ОУ) и выбора способа моделирования.
Базисом построения стала схема адаптивной системы, разработанная авторами [1]. В ее состав вошли: УС - узел сравнения напряжения задания с напряжением обратной связи ![]() ; П – пропорциональная цепочка; Г – генератор; СИ – ступенчатый интегратор (вместе – адаптивная цепочка); S - сумматор сигналов
; П – пропорциональная цепочка; Г – генератор; СИ – ступенчатый интегратор (вместе – адаптивная цепочка); S - сумматор сигналов ![]() ; converter U-> f – преобразователь напряжение – частота; АИ – автономный инвертор напряжения; АД – асинхронный двигатель; Н – насос; ОУ – объект управления; ИП – измеритель потенциала поверхности СПЖ.
; converter U-> f – преобразователь напряжение – частота; АИ – автономный инвертор напряжения; АД – асинхронный двигатель; Н – насос; ОУ – объект управления; ИП – измеритель потенциала поверхности СПЖ.
При рассмотрении выяснилось:
- необходимо чтобы регулятор своими действиями не только пропорционально управлял АД в данный промежуток времени, но и накапливал эту информацию для обеспечения изменения расхода заполнения, компенсирующего процессы релаксации накопленного заряда в объеме ![]() СПЖ. В результате достигается рост расхода с одновременным регулированием ЭСБ по потенциалу
СПЖ. В результате достигается рост расхода с одновременным регулированием ЭСБ по потенциалу![]() поверхности жидкости, для чего были введены параллельно пропорциональная (ПЦ) и интегральная (ИЦ) цепочки;
поверхности жидкости, для чего были введены параллельно пропорциональная (ПЦ) и интегральная (ИЦ) цепочки;
- звенья Converter, АИ и АД являются стандартными и описаны в литературе [2…4];
- необходимо чтобы ОУ функционировал также как при заполнении с постоянным установившемся расходом F=const. Это было достигнуто за счет анализа накопления заряда в объеме ![]() СПЖ, в результате чего была найдена функция роста потенциала φ=КФ f(F) при постоянном расходе [5], где КФ генерировало звено насоса, а функция определяла рост величины;
СПЖ, в результате чего была найдена функция роста потенциала φ=КФ f(F) при постоянном расходе [5], где КФ генерировало звено насоса, а функция определяла рост величины;
- насос, ИП, УС – пропорциональные звенья. У насоса расход зависит от угловой скорости w его вала. ИП – измерительный прибор определяет примерно линейную характеристику, а задание напряжения (5) управления - постоянная величина.
В результате входящий расход в ОУ перемножается с функцией нарастания потенциала поверхности СПЖ φ=КФ f(F), которые сбалансированы внутренними пропорциональными звеньями К. Тогда расход F генерирует потенциал поверхности УЖТ φ. Система замкнута жестко на УС.
Моделирование проведено в среде MatLab v.6.5. Исследование динамики процесса грузовой операции φ=f(t), показанное на рисункe (рис.2), проводилось при дискретизации структурной схемы управления двигателем насоса при снятии роста потенциала φ. Это позволило:
- в разомкнутой системе и использовании только пропорциональной цепочки, была получена функция нарастания потенциала, которая соответствует результату расчета сеточным методом заполнения постоянным установившемся расходом F=const (рис.2(а.1);2(б.1)) [5,6];
- в замкнутой системе и использовании только пропорциональной цепочки, ПЦ, была получена функция изменения потенциала по стандартной методике заполнения объемов СПЖ (рис.2(а.2);2(б.2)) [5,6];
- в случае замкнутой системы и наличии ИЦ, была получена функция стабилизации потенциала поверхности при max скорости заполнения (рис.2(а.3);2(б.3))[7].
Исследование системы при изменении величины задающего напряжения управления позволяет регулировать всем процессом на заданный уровень потенциала поверхности φ СПЖ, т.е. регулировать ЭСБ системы перегрузки.
Результат моделирования показывает рост расхода F и существенное снижение времени t проведения грузовой операции до 30%.
Основные результаты и выводы
Полученные результаты исследования позволяют утверждать, что автоматическая система управления перегрузкой УЖТ смоделирована и исследована.
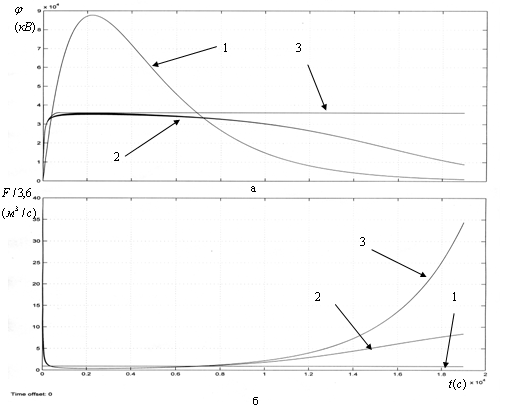
Рис.2. а,б – графики изменения потенциала и производительности
во времени при моделировании грузовой операции
Результат моделирования подтвердил теоретическое обоснование [1,5…7] и показал какая конфигурация в виде автомата может использоваться для реализации необходимого режима заполнения УЖТ в ТЕ.
ЛИтература
1. Якимчук Г.С., Кириллов О.Л., Якимчук С.Г. Адаптивная система управления частотно-регулируемым электроприводом объектов с медленно измняющимися параметрами // Материалы XVI Международной научно-технической конференции «Проблемы автоматизированного электропривода. Теория и практика». Тематический выпуск научно-технического журнала „ЭЛЕКТРОИНФОРМ” – Львів: ЕКОінформ, 2009.- 516с, - С.237-238.
2. Ключев В.И. Теория электропривода: Учебник для вузов.-М.: Энергоатомиздат, 1985г.-560с.:ил.
3. Теорія електропривода: Навч.посіб /М.Г.Попович та інш. -К.: Либідь, 1995, 494с.
4. Якимчук Г.С. Теорія автоматичного керування електромеханічними системами: Навч.посіб. К.: Вища Шк., 2009, 545с.:ил.
5. Галка В.Л. Электростатическая безопасность нефтеналивных судов и кораблей. – СПб.: Элмор. 1998. – 188с.
6. Проведение испытаний и исследований по оценке электростатической опасности при заполнении и механизированной мойке грузовых танков. Отчет по НИР (промежуточн), ЦНИИ–СЭТ, составлен на разработку ЦКБ «Изумруд» // –Херсон, –1993. –48с.
7. Кирилов О.Л., Якимчук Г.С. Оптимальное управление технологическим процессом заполнения слабопроводящими заряжающимися жидкостями (СПЗЖ) замкнутых объемов // Автоматика. Автоматизация. Электротехнические комплексы и системы. Херсон.- ХГТУ. – 2006. -№1(17).- C.120-131.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.