УДК 007.

Решение такой сложной проблемы, как моделирование коллективной операторской деятельности возможно лишь в той мере, в какой удается найти подходящие средства, т.е. язык для описания задачи, достаточно полно учитывающий ее специфику и обладающий вместе с тем необходимым уровнем абстракции, обеспечивающим приемлемую общность подхода.

В качестве первой серьезной проблемы, существенно затрудняющей разработку адекватных математических моделей операторской деятельности можно отметить отсутствие четко обоснованных и достаточно универсальных, содержательных моделей функционирования нервно-мышечного аппарата и мыслительных процессов человека, особенно на стадиях логической обработки предъявляемых сигналов и формирования решения.

Вторая группа проблем касается сознательного, творческого характера деятельности человека, существенным образом зависящей при прочих равных условиях от его личных субъективных данных, психофизиологического и эмоционального состояния, степени обученности и тренированности.

Третья группа проблем связана со способностями человека к самообучению и самоорганизации деятельности на базе предыдущего опыта. При создании математических моделей деятельности оператора в связи с этим возникают весьма трудные задачи адекватного отражения способностей человека к учету предыстории, интерполяции и экстраполяции контролируемых процессов, его адаптации к окружающей обстановке и выбору оптимальной стратегии поведения.

Четвертая группа проблем касается характеристик, присущих человеку как звену систем контроля и управления и связанных со свойственным человеку явлением запаздывания реакции по отношению к предъявляемому сигналу.

Пятая группа проблем вытекает из того факта, что и контролируемые процессы, и сама деятельность оператора, рассматриваемая как процесс, носит явно выраженный динамический характер, и потому они могут быть описаны надлежащим образом лишь в функциях, явно зависящих от времени.

К сожалению, значительная часть указанных выше проблем пока еще не получила достаточного отражения в существующих на сегодняшний день методиках моделирования операторской деятельности.

В настоящее время все, или, по крайней мере, значительная часть математических моделей деятельности человека в задачах управления, построенных на формализме теории автоматического управления, исходят из предположения о детерминированном характере этой деятельности. Необходимо отметить, что это предположение не оправдывается на практике даже в простейших ситуациях, относящихся к реакциям оператора на детерминированные сигналы, поскольку эти реакции явно случайны. Из других известных методов моделирования операторской деятельности следует отметить операционно-психофизиологический метод Г.М. Зараковского [3] и обобщенный структурный метод А.И. Губинского [1].

Первый из них основан на алгоритмическом описании трудовой деятельности оператора в форме логических схем. Алгоритм трудовой деятельности определяется как последовательность элементарных актов переработки информации и выполнения моторных действий вместе с логическими условиями перехода от одного акта к другому.

Применение обобщенного структурного метода ограничивается эргатическими системами, допускающими описание их функционирования в виде дискретных конечных алгоритмов, соответствующих схемам алгоритмов А.А. Ляпунова первого и второго рода. Представление алгоритмов осуществляется в виде совокупности специально введенных типовых функциональных единиц, для которых априори задаются необходимые числовые характеристики. Математическими моделями этого класса систем являются стохастические сети с петлями и циклами (поглощающие полумарковские цепи с произвольными законами распределения времени между переходами).

Существенными недостатками указанных выше методов является отсутствие учета динамики процесса, а также малая общность, связанная с необходимостью задания алгоритма деятельности. Если говорить о моделировании коллективной деятельности операторов, то современное состояние этой проблемы находится на еще более низком уровне. Из известных нам работ, можно отметить лишь работы [4,5] , в которых в рамках имитационного моделирования построены модели коллективного поведения.

Учитывая недостатки описанных выше методов, наиболее перспективными, с нашей точки зрения, направлением моделирования операторской деятельности является направление, основанное на принципах искусственного интеллекта [7]. При таком подходе алгоритмы переработки информации, заложенные в математической модели, могут и отличатся от алгоритмов, используемых человеком, однако математическая модель должна удовлетворять основным принципам теории эргатических систем.

В соответствии со сказанным выше, в качестве первого приближения к созданию модели на принципах искусственного интеллекта математическую модель рассматриваемой системы будем искать в классе самоорганизующихся систем управления с функциональной адаптацией.

В нашем случае имеется трехуровневая иерархическая система управления со связями между элементами системы одного уровня, подчиненных одному элементу следующего уровня по принципу «каждый с каждым», а между элементами разных уровней – по подчиненности.

Блок-схема предлагаемой модели показана на рис.1., где в целях упрощения операторы первого уровня управления показаны в виде бригад, поскольку модели каждого из них аналогичны.

Функционирование модели происходит следующим образом. Ошибка слежения поступает на блок взаимопомощи, который определяет, к какому конкретному оператору первого уровня следует ее направить. Непосредственно поступающая к оператору ошибка e попадает на блок принятия решения, вырабатывается управляющее воздействие U ¹ ,воздействующее через блок взаимопомощи на управляемый процесс.

Блок принятия решения работает в режиме функциональной адаптации, которая происходит в результате оценки показателя функционирования. В математическую модель операторов первого уровня входит также блок оценки напряженности работы операторов.

С первого уровня на второй поступает информация об информационной напряженности работы операторов С и об ошибках слежения e. На основе этой информации в блоке оценки вероятности выполнения задания вычисляется значение вероятности выполнения задания каждым оператором Р_вз . На основании информации о вероятностях выполнения задания и об информационных напряженностях работы операторов принимается решение о взаимопомощи. В случае, если возможность взаимопомощи отсутствует, оператор второго уровня принимает решение об оказании помощи, которую осуществляет он сам при помощи управляющего воздействия U ². Блок принятия решения о помощи работает в режиме функциональной адаптации.

Со второго уровня управления информация о вероятности выполнения задания поступает на третий уровень управления на блок прогнозирования, в котором осуществляется прогноз вероятности выполнения задания на заданное время. Информация о прогнозируемой вероятности выполнения задания Р_вз∆t поступает на блок принятия решения, вырабатывающий управляющие воздействия U ². Блок принятия решения третьего уровня также работает в режиме функциональной адаптации, которая осуществляется по результатам оценки показателя функционирования.

В соответствии с приведенным выше математическим описанием приведен алгоритм функционирования модели.

Здесь блоки (1-7) описывают поведение операторов первого уровня управления. Блок 3 соответствует модели отслеживаемого процесса X, который генерируется n-мерный генератором случайных чисел. В блоке 4 вычисляется ошибка слежения . В блоке (5) строится матрица взаимопомощи L. В блоках (6) вычисляется ошибка , поступающая к конкретному оператору, выбор которого определяется матрицей L, а также воздействие , которое через матрицу поступает ко входу процесса. В блоке 7 вычисляется текущее время t, прошедшее от начала процесса слежения, где интервал времени  характеризует запаздывание, свойственное человеку-оператору.

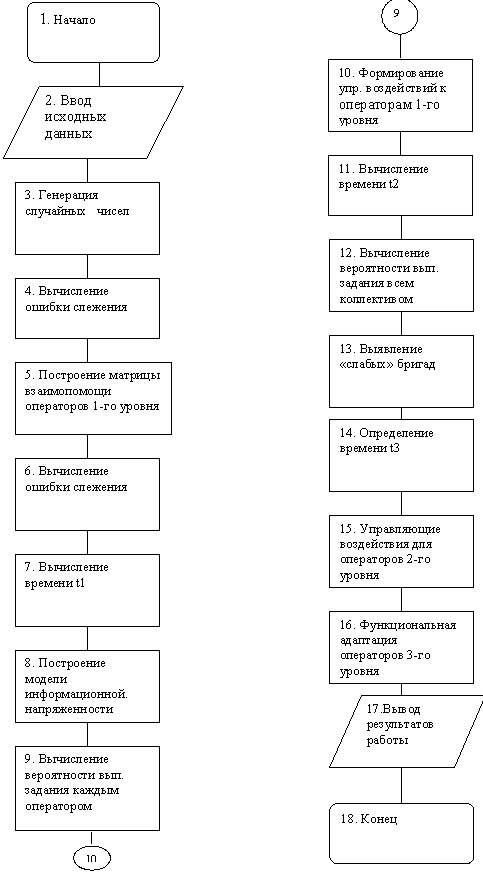
Рис. 1 Блок – схема функционирования трехуровневой иерархической системы управления

По истечении времени , равном

и после прохождения информации через блоки, соответствующие моделям информационной напряженности операторов второго и третьего уровня управления, информация поступает на блоки (8-10), которые определяют режим самонастройки операторов первого уровня. Время характеризует время, необходимое оператору для оценки качества его деятельности. После настройки коэффициентов процесс слежения продолжается, начиная с блока 3, путем выборки нового вектора Х.

Модель информационной напряженности работы операторов описывается блоком (8). Здесь по известным N значениям случайных процессов  и Х вычисляются средние значения  и , корреляционные матрицы К и , матрицы спектральных плотностей  и и наконец, вектор информационной напряженности работы операторов С.

Блоки (9-11) относятся к моделям операторов второго уровня управления. В блоке (9) вычисляется вероятность выполнения задания каждым оператором второго уровня. В блоке (10) выбираются операторы, которым необходимо показывать помощь и операторы, которые будут оказывать эту помощь, для чего строятся матрицы , а также формируется управляющее воздействие ,поступающее к операторам первого уровня.

В блоке 12 проверяется текущее время , которое равно

где

Здесь время  определяет запаздывание операторов второго уровня, а - время, необходимое оператору второго уровня для оценки качества его деятельности.

По истечении времени  и прохождения информации через блоки модели третьего уровня информация поступает на блоки, в которых осуществляется процесс функциональной адаптации операторов второго уровня управления. После настройки коэффициентов информация поступает на блоки формирования управляющего воздействия .

К модели операторов третьего уровня относятся блоки (12-15). В блоке (12) вычисляется значение вероятности выполнения задания всем коллективом, прогнозируемое на время . В случае, если прогнозируемое значение меньше допустимого значения, то выявляются «слабые» бригады по прогнозируемым значениям и вероятностей выполнения задания, что производится в блоке (13) выявляются «слабые» операторы в «слабых» бригадах по прогнозируемым значениям их вероятностей выполнения задания. В блоке 14 проверяется текущее время , которое равно

где

Здесь время  определяет запаздывание оператора третьего уровня, а  - время, необходимое оператору третьего уровня для оценки качества его деятельности.

По истечении времени информация поступает на блоки (16-18), в которых осуществляется процесс функциональной адаптации оператора третьего уровня. В блоке (16) вычисляются управляющие воздействия, вырабатываемые оператором третьего уровня.

Вышеописанная модель может быть использована при решении задач управления различными производственными коллективами.

1.                  Губинский А.И. Эргономическое проектирование судовых систем управления /А.И. Губинский, В.Г. Евграфов –Л: Судостроение, 1977. – 224 с.

2.                  Дюк В.А. Компьютерная психодиагностика. – Санкт-Петербург «Братство», 1994. – 364 с.

3.                  Зароковский Г.М. Психофизиологический анализ трудовой деятельности: Логическо-вероятностный подход при изучении труда управляющего типа.- М.:Наука, 1966. – 114 с.

4.                  Зигель А., Вольф Дж. Модели группового поведения в системе человек-машина. –М.: Мир, 1973. –261 с.

5.                  Иванов-Муромский К.А. и др. Психофизиология оператора в системах человек-машина/ К.А. Иванов-Муромский, О.Н. Лукьнова, В.А. Черноморец и др. – Киев: Наук. думка, 1980. – 344 с.

6.                  Трофимов Ю.Л. Инженерная психология. – Киев, «Либідь», 2002. – 264 с.

7.                  Уинстон П. Искусственный интелект. – М.:Наука, 1980. – 520 с.