УДК 621.316.37.
ПРИЛОЖЕНИЕ ПОЛОЖЕНИЙ ТЕОРИИ ДРОССЕЛЯ И ТРАНСФОРМАТОРА К РАСЧЕТУ И АНАЛИЗУ ЭЛЕКТРОМАГНИТОМ ПЕРЕМЕННОГО ТОКА
Китаев А.В., Сушич Е.Ф.
Вопросу исследования электромагнитов переменного тока уделено большое внимание в курсе "Электрические аппараты" [1-5]. Однако анализ их поведения построен столь своеобразно, что создается впечатление о электромагнитах, как самостоятельной группе устройств, которая с дросселями и трансформаторами не имеет явно выраженной общности. В то же время в ТОЭ [6,7], где закладываются основы теории дросселя и трансформатора, указывается, на очевидность их приложения к исследованию аналогичных устройств (электромагнитов, электрических машин и т.д.). Ниже предлагается построить изложение затронутого вопроса так, чтобы произошло единение двух научных направлений на основе принципов системности и преемственности.
Пусть исследуемый электромагнит имеет магнитную цепь, конфигурация которой приведена на рис.1.
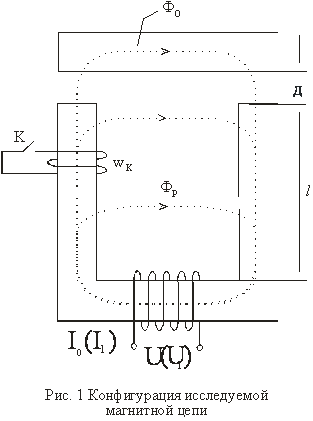
Тогда при условии разомкнутого рубильника К он представляет собой обычный дроссель, анализ которого выполняется при условии, что известны: напряжение сети питания ![]() , геометрические размеры сердечника, его материал, семейство петель гистерезиса и основная кривая магнитной индукции, проходящая через вершины этих петель. В случае электромагнита перечень исходных данных расширяется, поскольку считаются известными поток воздушного зазора
, геометрические размеры сердечника, его материал, семейство петель гистерезиса и основная кривая магнитной индукции, проходящая через вершины этих петель. В случае электромагнита перечень исходных данных расширяется, поскольку считаются известными поток воздушного зазора ![]() и габаритные размеры катушки, в соответствии с которыми устанавливается средняя длина витка
и габаритные размеры катушки, в соответствии с которыми устанавливается средняя длина витка ![]() и площадь окна обмотки
и площадь окна обмотки ![]() . Это обстоятельство существенно упрощает анализ электромагнита по сравнению с дросселем, но не меняет его целевого назначения: определение м.д.с. обмотки
. Это обстоятельство существенно упрощает анализ электромагнита по сравнению с дросселем, но не меняет его целевого назначения: определение м.д.с. обмотки ![]() и ее числа витков
и ее числа витков ![]() . Для решения задачи воспользуемся системой основных уравнений дросселя, которая согласно метода эквивалентных синусоид записывается в комплексной форме:
. Для решения задачи воспользуемся системой основных уравнений дросселя, которая согласно метода эквивалентных синусоид записывается в комплексной форме:
|
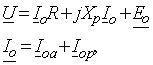
где ![]() соответственно активное и индуктивное сопротивление обмотки;
соответственно активное и индуктивное сопротивление обмотки;
![]() э.д.с. от магнитного потока
э.д.с. от магнитного потока ![]() ;
;
![]() соответственно активная и реактивная составляющие тока
соответственно активная и реактивная составляющие тока ![]() ; является основой для составления схемы замещения и построения векторной диаграммы дросселя (электромагнита) (см. рис. 1).
; является основой для составления схемы замещения и построения векторной диаграммы дросселя (электромагнита) (см. рис. 1).
Составляющая тока ![]() определяется по результатам расчета магнитной цепи согласно методике, приведенной в
определяется по результатам расчета магнитной цепи согласно методике, приведенной в ![]() . Итогом расчета является равенство:
. Итогом расчета является равенство:
![]()
где ![]() - магнитная напряженность воздушного зазора
- магнитная напряженность воздушного зазора ![]() ;
;
![]() - магнитная напряженность участка
- магнитная напряженность участка ![]() (при числе участков равном
(при числе участков равном ![]() );
);
![]() - длина участка
- длина участка ![]() .
.
Отсюда следует, что
![]() (3)
(3)
На основании данных того же расчета определяются потери в стали сердечника:
![]()
где ![]() - коэффициент, учитывающий увеличение потерь из-за наклепа при штамповке и при выполнении других технологических операций.
- коэффициент, учитывающий увеличение потерь из-за наклепа при штамповке и при выполнении других технологических операций.
![]() - потери в стали при частоте
- потери в стали при частоте ![]() Гц и магнитной индукции 1,0Tл;
Гц и магнитной индукции 1,0Tл;
![]() - амплитуда магнитной индукции на участке
- амплитуда магнитной индукции на участке ![]() ;
;
![]() - масса участка
- масса участка ![]() ;
;
![]() - показатель степени, зависящий от марки стали.
- показатель степени, зависящий от марки стали.
Значения ![]() ,
, ![]() и
и ![]() для электротехнических сталей найдены экспериментальным путем и берутся согласно данным таблицы:
для электротехнических сталей найдены экспериментальным путем и берутся согласно данным таблицы:
|
Марка стали |
|
|
|
|
2011, 2013, 2211 2312 2411 |
для всех марок
|
1,75 1,6 |
1,5 1,4 1,3 |
При известном значении ![]() составляющая тока
составляющая тока ![]() рассчитывается по формуле:
рассчитывается по формуле: ![]() и тогда модуль тока
и тогда модуль тока ![]() .
.
Если сопоставить между собой формулу (3), а также соотношения для ![]() и
и ![]() :
:
![]()
где ![]() - сечение провода;
- сечение провода; ![]() - удельная проводимость для потока рассеяния;
- удельная проводимость для потока рассеяния; ![]() - высота стержня; то окажется, что все они зависят от
- высота стержня; то окажется, что все они зависят от ![]() , которое подлежит определению. Отсюда возникает возможность поиска
, которое подлежит определению. Отсюда возникает возможность поиска ![]() на основе таблично-графического метода. С этой целью определяется предварительное (расчетное) и явно завышенное число витков
на основе таблично-графического метода. С этой целью определяется предварительное (расчетное) и явно завышенное число витков ![]() при условии, что составляющие
при условии, что составляющие ![]() и
и ![]() уравнения (1) пренебрежимо малы:
уравнения (1) пренебрежимо малы:
![]()
Тогда ![]() и
и ![]() приобретают конкретные числовые значения, которые заносятся в таблицу, и на их основе выполняется проверка равенства, составленного на основании теоремы косинусов для модулей векторов, уравнения (1):
приобретают конкретные числовые значения, которые заносятся в таблицу, и на их основе выполняется проверка равенства, составленного на основании теоремы косинусов для модулей векторов, уравнения (1):
![]()
где ![]() - аргумент комплексного сопротивления обмотки;
- аргумент комплексного сопротивления обмотки;
![]() - модуль комплексного сопротивления обмотки;
- модуль комплексного сопротивления обмотки;
![]() - Угол сдвига между векторами
- Угол сдвига между векторами ![]() и
и ![]() ;
;
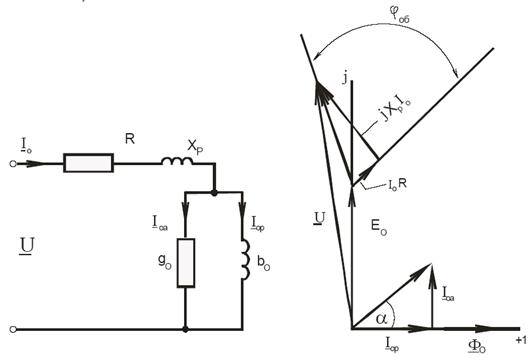
а) б)
Рис. 2 Схема замещения и векторная диаграмма магнита (дросселя)
Разумеется, что при ![]() равенства между правой и левой частью принципиально не может быть. Поэтому расчет следует продолжить при
равенства между правой и левой частью принципиально не может быть. Поэтому расчет следует продолжить при ![]() и т.д. По результатам расчета строится зависимость правой части
и т.д. По результатам расчета строится зависимость правой части ![]() функции число витков
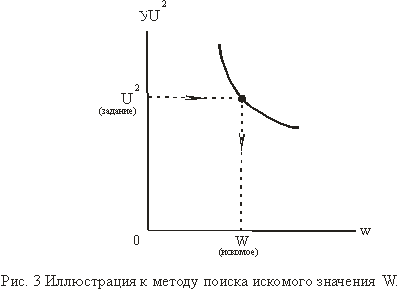
функции число витков ![]() (см. рис.3). Затем на оси ординат откладывается значение
(см. рис.3). Затем на оси ординат откладывается значение ![]() и проводится линия, параллельная оси абсцисс. Перпендикуляр, опущенный из точки пересечения этой линии с расчетной кривой на ось абсцисс, и даст искомое значение
и проводится линия, параллельная оси абсцисс. Перпендикуляр, опущенный из точки пересечения этой линии с расчетной кривой на ось абсцисс, и даст искомое значение ![]() , а соответственно с ним определится и величина м.д.с.
, а соответственно с ним определится и величина м.д.с. ![]() .
.
При известном ![]() можно дать ответ на вопрос о сечении провода
можно дать ответ на вопрос о сечении провода ![]() под обмотку и его диаметре
под обмотку и его диаметре ![]() , используя соотношения:
, используя соотношения:
![]()
где ![]() - коэффициент заполнения обмотки.
- коэффициент заполнения обмотки.
Затем вся обмотка проверяется на критерий обеспечение допустимой температуры нагрева ![]() по рекомендациям, изложенным в
по рекомендациям, изложенным в ![]()
Перейдем к анализу работы того же электромагнита при замкнутомположении ключа К, т.е. при наличии короткозамкнутой обмотки. В таком случае устройство представляет собой обычный трансформатор в режиме к.з., поведение которого описывается следующей системой уравнений:
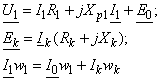
где ![]() - напряжение и ток обмотки, подключенной к зажимам источника (назовем ее первичной);
- напряжение и ток обмотки, подключенной к зажимам источника (назовем ее первичной);
![]() - активное и индуктивное сопротивление рассеяния той же первичной обмотки;
- активное и индуктивное сопротивление рассеяния той же первичной обмотки;
![]() - активное и индуктивное сопротивление рассеяния короткозамкнутой (вторичной) обмотки;
- активное и индуктивное сопротивление рассеяния короткозамкнутой (вторичной) обмотки;
![]() - э.д.с., наводимая во вторичной обмотке основным магнитным потоком;
- э.д.с., наводимая во вторичной обмотке основным магнитным потоком;
![]() - м.д.с. соответственно первичной и вторичной обмоток;
- м.д.с. соответственно первичной и вторичной обмоток;
![]() - м.д.с. первичной обмотки при отсутствии вторичной.
- м.д.с. первичной обмотки при отсутствии вторичной.
![]() - число витков первичной и короткозамкнутой обмотки.
- число витков первичной и короткозамкнутой обмотки.
После выполнения операции приведения та же система уравнений трансформатора перепишется в виде:
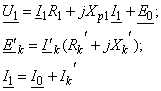
где ![]() - приведенные к числу витков первичной обмотки значения
- приведенные к числу витков первичной обмотки значения ![]()
Последней системе уравнений соответствует схема замещения и векторная диаграмма, приведенные на рис. 4.
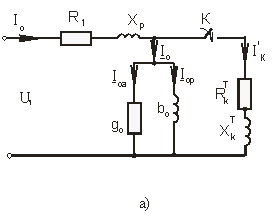
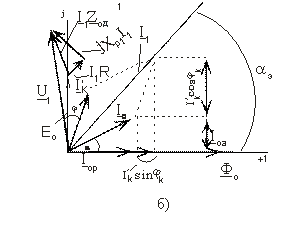
Рис. 4 Схема замещения и векторная
диаграмма электромагнита с
к.з. обмоткой
Из сопоставления схем замещения рис.2 и 4 следует, что они отличаются друг от друга только наличием ветви с последовательно включенными сопротивлениями ![]() , которая, естественно, оказывает влияние на показатели работы первичной цепи. В частности она вызывает увеличение тока
, которая, естественно, оказывает влияние на показатели работы первичной цепи. В частности она вызывает увеличение тока ![]() , значение которого согласно векторной диаграмме рис. 4б определятся соотношением:
, значение которого согласно векторной диаграмме рис. 4б определятся соотношением:
![]()
где ток ![]() и аргумент полного комплексного сопротивления вторичной обмотки
и аргумент полного комплексного сопротивления вторичной обмотки ![]() рассчитываются по формулам:
рассчитываются по формулам:

Методика расчета числа витков ![]() тем не менее, здесь полностью сохраняется, лишь в уравнении баланса квадратов напряжений, записанных на основании теоремы косинусов, аргумент
тем не менее, здесь полностью сохраняется, лишь в уравнении баланса квадратов напряжений, записанных на основании теоремы косинусов, аргумент ![]() меняется на
меняется на ![]() вычисляемый по соотношению:
вычисляемый по соотношению:
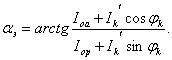
Из конструктивных соображений к.з.обмотка часто выполняется в виде латунной или медной гильзы, т.е. с ![]() . В таком случае величина
. В таком случае величина ![]() пренебрежимо мала и формула для токов
пренебрежимо мала и формула для токов ![]() и аргумента
и аргумента ![]() получают предельно простой вид:
получают предельно простой вид:
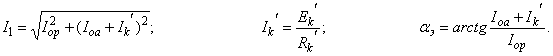
![]()
В работе ![]() на основании сходства токов
на основании сходства токов ![]() и
и ![]() по характеру действия дано вполне логичное предложение, что потери в стали можно рассматривать, как потери в некоторой фиктивной к.з.обмотке, содержащей только активное сопротивление. Это привело к необходимости введения понятий активного, реактивного и комплексного магнитного сопротивления и обоснования методики их расчета. В нашем случае изложение указанного материала становится ненужным в связи с законченностью анализа.
по характеру действия дано вполне логичное предложение, что потери в стали можно рассматривать, как потери в некоторой фиктивной к.з.обмотке, содержащей только активное сопротивление. Это привело к необходимости введения понятий активного, реактивного и комплексного магнитного сопротивления и обоснования методики их расчета. В нашем случае изложение указанного материала становится ненужным в связи с законченностью анализа.
Для снижения пульсации силы тяги на практике часто поступают так, что к.з.виток охватывает лишь часть площади торца магнитопровода, т.е. одна из его сторон находится в специально выполненном пазу. В таком случае для удобства анализа и расчета конфигурацию магнитной цепи целесообразно представить в виде совмещения дросселя и трансформатора, сердечники которых находятся под действием одной м.д.с. (см. рис.5).
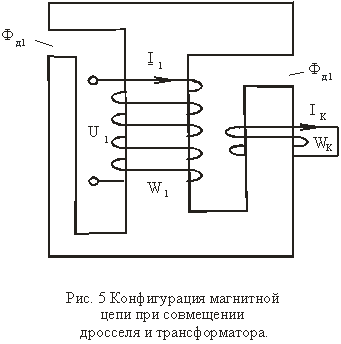
Тогда получится схема замещения, приведенная на рис.6. Поскольку в дросселе магнитный поток ![]() и ток
и ток ![]() сдвинуты на угол
сдвинуты на угол ![]() , а в трансформаторе угол между
, а в трансформаторе угол между ![]() и
и ![]() равен
равен ![]() , то при одной и той же м.д.с.
, то при одной и той же м.д.с. ![]() сдвинутыми между собой на угол
сдвинутыми между собой на угол ![]() окажутся магнитные потоки
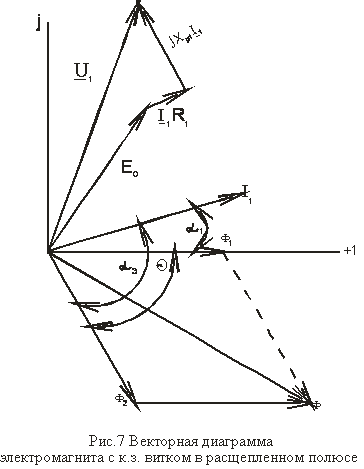
окажутся магнитные потоки ![]() и
и ![]() (см.рис.7). Каждый из этих потоков создаст свою силу тяги, соответственно
(см.рис.7). Каждый из этих потоков создаст свою силу тяги, соответственно ![]() и
и ![]() . Их мгновенные значения запишутся:
. Их мгновенные значения запишутся:
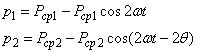
где 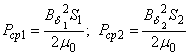
![]() - магнитные индукции в зазорах дросселя и трансформатора;
- магнитные индукции в зазорах дросселя и трансформатора;
![]() - площадь соответственно в дросселе и трансформаторе.
- площадь соответственно в дросселе и трансформаторе.
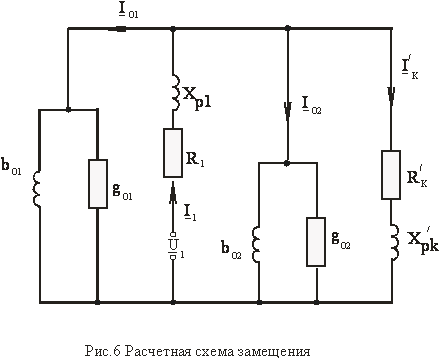
Результирующая сила ![]() , действующая на якорь, равна сумме
, действующая на якорь, равна сумме ![]() и
и ![]() , т.е.
, т.е. ![]() . Это означает, что результирующее усилие пульсирует, но не от максимума до нуля, как ее составляющие, а от максимального усилия
. Это означает, что результирующее усилие пульсирует, но не от максимума до нуля, как ее составляющие, а от максимального усилия ![]() до минимального
до минимального ![]() , которое больше нуля. Для определения
, которое больше нуля. Для определения ![]() и
и ![]() исследуем функцию
исследуем функцию ![]() на экстремум по переменной t , полагая
на экстремум по переменной t , полагая ![]() , что в принципе можно обеспечить за счет варьирования
, что в принципе можно обеспечить за счет варьирования ![]() .В итоге получим, что экстремумы имеют место при условии:
.В итоге получим, что экстремумы имеют место при условии: ![]() где
где ![]() - номера полупериодов. Подстановкой этого условия в выражение для
- номера полупериодов. Подстановкой этого условия в выражение для ![]() получим:
получим:
![]()
Очевидно, что при ![]() будет выполнено равенство
будет выполнено равенство ![]() и
и ![]() , т.е. пульсации исчезнут. Но, чтобы добиться такого результата нужно обеспечить равенство потерь в стали нулю и чисто активное сопротивление к.з. витка при отсутствии намагничивающего тока. Практических решений на этот счет нет, и потому реально достижимые значения угла
, т.е. пульсации исчезнут. Но, чтобы добиться такого результата нужно обеспечить равенство потерь в стали нулю и чисто активное сопротивление к.з. витка при отсутствии намагничивающего тока. Практических решений на этот счет нет, и потому реально достижимые значения угла ![]() лежат в пределах
лежат в пределах ![]() . Следовательно, отношение
. Следовательно, отношение ![]() к
к ![]() равно примерно трем, а амплитуда переменной составляющей пульсации не превышает
равно примерно трем, а амплитуда переменной составляющей пульсации не превышает ![]() . Разумеется, что для обеспечения надежной работы электромагнита
. Разумеется, что для обеспечения надежной работы электромагнита ![]() должно быть больше усилия возвратной пружины.
должно быть больше усилия возвратной пружины.
Таким образом, базируясь на положения ТОЭ по вопросу анализа дросселей и трансформаторов, можно построить анализ электромагнитов переменного тока в простой, компактной форме, сохраняя системность и преемственность и устраняя излишние искусственные построения.
It is shown in work, that examining the electromagnets of alternating current within the framework of single family of such electrical engineering devices, as throttles and transformers, it is possible to build their analysis in a simple and compact form. The same is achieved communication of such scientific directions, as the "Electric vehicles" and TBE on the basis of principles of the system and succession.
1. Буль Б.К. и др. Основы теории электрических аппаратов. Под ред. Г.В. Буткевича. -М.: "Высшая школа", 1970, 600 с.
2. Марков З.Т. Судовые электрические аппараты. -Л..«Судостроение»:1971, 390 с.
3. Новиков 10.Н, Теория и расчет электрических аппаратов. -Л.:"Энергия", 1970,328 с.
4. 4-. Таев И,С. и др. Основы теории электрических аппаратов. -М.: "Высшая школа", 1987, 352 с.
5. Чунихин А.А. Электрические аппараты. -М.: "Энергоатамиздат", 1988,
6. 720 с.
7. Бессонов Л.А. Теоретические основы электротехники. -М.:"Высшая школа", 1988,630 с.
8. Зевеке Г.В. Основы теории цепей. -М.: "Энергия", 1975, 722 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.