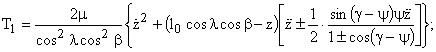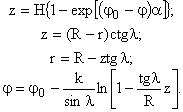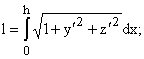УДК 677.054.12.004
МОДЕЛИРОВАНИЕ НАТЯЖЕНИЯ НИТИ ПРИ СМОТКЕ С КОНИЧЕСКОЙ БОБИНЫ В ПРОЦЕССЕ ПАРТИОННОГО СНОВАНИЯ
Клименко Д.С.
Натяжение паковки, как функция её линейной скорости и еще целого ряда технологических факторов, до сих пор до конца не изучена. Поэтому задача управления осложняется наличием у объекта управления релейных и медленноменяющихся характеристик (торможение в случае обрыва и медленно растущие радиус паковки, моменты сил инерции и трения).
Существует ряд работ, посвященных моделированию процесса снования, исследованию обрывности нитей при партионном сновании и разнообразным способам оптимизации данного процесса. Однако рассмотренные модели опираются на обобщенные сведения о технологии и не могут быть применены на практике. Статьи, посвященные исследованию колебательных составляющих натяжения, ограничиваются моделированием небольших технологических участков нити на пути от бобины до сновального вала.
Целью статьи является создание модели, наиболее точно описывающей процессы изменения натяжения при сматывании нити с конической бобины. Планируется применение полученной модели для описания всего процесс снования.
В [1] приводится формулы, описывающие изменение геометрических параметров конической бобины как функций длинны смотанной нити. Такой подход позволяет проводить точное определение радиусов паковки непосредственно на станке, опираясь лишь на априорные измерения, модель геометрических параметров и показания датчика длинны смотанных нитей.
Описание движения нити под действием натяжения начинается с определения точки касания. В [2] рассмотрены три типовые пространственные траектории. Результаты показывают высокую точность моделирования при использовании локсодромы:
|
|
(1) |
|
где ρ, φ, ζ- |
цилиндрические координаты, ось которых совпадает с осью кругового конуса, |
|
α- |
Угол между линией намотки и образующей конуса в точке начала движения. |
|
|
(2) |
|
где H - |
высота конуса; |
|
R - |
радиус основания. |
Цикл намотки считается законченным, когда ρк≈0.
Сложность при определении координат точки схода нити с бобины заключается в определении медленноменяющейся максимальной длинны дуги на конической поверхности, требующей взятия конечного интеграла в полярных координатах, что в свою очередь связано с затратами вычислительных мощностей.
При исследовании процесса осевого сматывания нити с неподвижной паковки важно определить начальное натяжение нити в зоне отрыва её от поверхности. В [3] приведена формула, определяющая величину реактивной составляющей силы натяжения нити при сматывании её с неподвижной паковки в зависимости от контурной скорости движения её в баллоне, от геометрических параметров паковки и баллона и от положения точки схода нити на поверхности паковки.
|
|
(3) |
|
|
|
где |
реактивная составляющая силы натяжения; |
|
μ - |
линейная плотность нити; |
|
l- |
длина баллонирующего участка нити; |
|
γ- |
угол между элементом нити dl и осью z. |
|
λ- |
угол при вершине конуса; |
|
β- |
угол намотки; |
|
R- |
радиус основания конуса; |
|
l0- |
длина витка нити на паковки между точек с координатами z0 и zmax; |
Верхний знак соответствует значению силы при убывающей массе, когда точка схода нити движется вверх, нижний знак – при возрастающей массе, когда точка схода движется вниз.
Координаты z, φ и r связаны соотношением
|
|
(4) |
Уравнение натяжения нити в баллоне при сматывании с початка имеет следующий вид [4]:
|
|
(5) |
|
где Тx - |
натяжение нити в любой точке баллона; |
|
Т1 - |
натяжение нити при сматывании с початка; |
|
R - |
радиус паковки в точке сматывания; |
|
r - |
радиус баллона. |
Натяжение нити в вершине баллона, где r = 0, равно:
|
|
(6) |
Данная формула применима для описания смотки нити с конической бобины. Угловая скорость точки схода баллонирующей нити описывается формулой
|
|
(7) |
Массу нити в баллоне можно определить, зная линейную плотность нити и определив по формуле [5]:
|
|
(8) |
Из уравнения (5) видно, что натяжение нити в любой точке баллона равно натяжению нити в точке отделения ее от паковки (Т1) плюс динамическая составляющая, равная половине произведения массы 1 см нити на квадрат угловой скорости и на разность квадратов радиуса паковки и радиуса определяемой точки баллона.
Из этого уравнения следует, что наименьшим натяжение нити будет в самой удаленной точке от оси баллона и наибольшим - в точке пересечения нити с осью вращения баллона.
Выводы
1. На основании приведенных формул, для исследования колебаний натяжения нити с неподвижной конической бобины в процессе снования, составлена модель в пакете Matlab. Следует отметить, что моделирование проводится без учета таких параметров, как угол наклона бобины в шпулярнике, сил трения при отрыве нити от паковки, а также цеховых влажности и температуры. Рассматривается плоская форма баллона. Каждый этап моделирования выполнен отдельным блоком, что позволяет легко вносить изменения и уточнения а также отслеживать зависимости изменения параметров модели от линейной скорости снования.
2. Модель предназначена для исследования колебаний натяжения нити при партионном сновании с конических бобин. Конечной целью моделирования является исследование влияния колебательных составляющих натяжения (параметрической и вынужденно) на обрывность при различных динамических режимах процесса снования.
1. Моделирование сматывания с конической бобины при партионном сновании / Клименко Д.С. // Проблемы легкой и текстильной промышленности Украины. – 2004. - №1(8). - С. 323
2. Водовозов В.М., Мядзель В.Н., Рассудов Л.Н. Планирование траекторий и разработка упрощенных законов управления намоточным оборудованием при замотке конических паковок. – Изв. вузов. Технология текстильной промышленности, – 1980. – №3 . - с.81-84.
3. Чичаева С.А., Кан Э.М. О реактивной составляющей силы натяжения при сматывании нити с неподвижной паковки. – Изв. вузов. Технология текстильной промышленности, – 1972. – №5 с.78-81.
4. А. И. Бородин Высокоскоростное перематывание основной пряжи с початка. – М.: “Легкая индустрия”, – 1965.
5. Якубовский Ю.В., Живов В.С., Коритысский Я.И., Мигушов И.И. Основы механики нити. – М.: “Легкая индустрия”,– 1973.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.