Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 62-50

ЗАСТОСУВАННЯ КОМІТЕТАМИ ЕКСПЕРТІВ СИСТЕМИ НЕЧІТКОГО ЛОГІЧНОГО ВИВОДУ ІЗ ЗВАЖЕНОЮ ІСТИННІСТЮ.

Коршевнюк Л.О.

Вступ. В задачах прийняття рішень, при моделюванні та формальному описі гуманістичних систем, зокрема економічних та соціальних, у функціонуванні яких приймає участь людина, стикаються з проблемою домінування якісних, погано визначених факторів, які виявляються у невизначеностях, нечітких, неточних, розпливчастих властивостях процесів та явищ. Існуючі детерміновані підходи з використанням точних характеристик об’єктів, явищ та процесів, точних методів моделювання та прийняття рішень і процедур оптимізації не враховують зазначені фактори, тому не можуть бути успішно використані при моделюванні реальних процесів.

Для вирішення зазначеної проблеми користуються технологіями штучного інтелекту. Достатньо популярним є розв’язання практичних задач багатокритеріального оцінювання і вибору за допомогою систем, що базуються на теорії нечітких множин (ТНМ) та нечіткій логіці Л.Заде [1]. Нечітка логіка припускає те, що логіка оперує приблизними поняттями, що робить її подібною до людських міркувань. Істиннісний функціонал в НЛ приймає значення з відрізку . Доцільно зазначити, що виходячи з публікацій у відкритих джерелах серед неперервнозначних логік у світі немає рівних нечіткій логіці Л.Заде, як за розробленістю, так і за кількістю застосувань.

Крім того, зрозуміло, що для прийняття якісних рішень в реальних задачах слід спиратись на досвід, знання та інтуїцію фахівців-експертів, тому на практиці вдаються до спільного використання підходів штучного інтелекту та методів експертних оцінок [2,3,4].

Серед практичних задач прийняття рішень одними з найактуальніших у різних галузях діяльності людини постають задачі багатокритеріального оцінювання і вибору комітетом експертів. Так, наприклад, в економічних системах такими задачами є задачі розподілу ресурсів, задачі оптимізації «портфелю», задачі вибору рішень з множини альтернативних варіантів, тощо.

У загальному випадку задача багатокритеріального групового експертного оцінювання і вибору формулюється наступним чином. Нехай є множина запропонованих об’єктів ,  та комітет осіб, що приймають рішення, (ОПР) , . Необхідно з множини об’єктів вибрати ті, що у найкращий спосіб відповідають деякій заданій цілі.

Загальна схема розв’язання таких задач виглядає наступним чином. Для об’єктів  комітетом ОПР  експертним способом визначається набір важливих критеріїв , , за якими буде проводитись оцінювання об’єктів [3]. Визначені критерії , , за якими ОПР будуть оцінювати проекти, можуть відрізнятися своєю важливістю, та в результаті, мати різну вагу впливу на рішення задачі. Більш того, кожна ОПР може мати свій погляд на ранжирування та розподіл ваг критеріїв, тому доцільно, щоб кожна ОПР  надавала свої індивідуальні вагові коефіцієнти  для кожного критерію , де , . Окрім цього, доцільним постає врахування значимості, досвіду, рівню підготовки, посади, тощо кожної ОПР. Для цього ОПР  колегіально, чи, як правило, керівником комітету – особою, що є відповідальною за прийняте рішення, завдаються вагові коефіцієнти  для ОПР , .

Кожному об’єкту ,  кожною ОПР ,  за кожним критерієм ,  надаються окремі суб’єктивні експертні оцінки . Зазначимо, що перевага за одним із критеріїв не залежить від того, які значення приймають оцінки певного об’єкту за іншими критеріями [4,5].

Отже, задача, що розглядається, є задачею багатокритеріального вибору об’єктів комітетом експертів. Для реальних практичних задач зручним та прийнятним є використання підходу зведення задачі багатокритеріального вибору до задачі однокритеріального вибору [4,5], тобто вибір об’єктів буде відбуватись за узагальненою агрегованою оцінкою кожного об’єкту  – ступенем привабливості ,  до загальної цілі.

Для знаходження узагальнених агрегованих оцінок об’єктів з урахуванням  невизначеностей, які, як вже зазначалось, дуже характерні для такого класу задач, зручним є використання системи нечіткого логічного виводу (НЛВ) [4,6].

Система НЛВ для одержання узагальнених оцінок об’єктів має  входів (кількість критеріїв оцінювання), та один вихід – власне узагальнена оцінка об’єкту. Система НЛВ використовується для кожного об’єкту ,  та для кожної ОПР ,  окремо, тобто система НЛВ відпрацьовує  циклів. За один цикл на вхід системи НЛВ подаються оцінки  за критеріями  об’єкту  від ОПР , де . На виході система видає узагальнену чітку оцінку  об’єкту  від ОПР .

Потім на основі узагальнених за критеріями оцінок  та вагових коефіцієнтів  ОПР, де , , здійснюється операція знаходження остаточної агрегованої оцінки кожного об’єкту  – ступенем привабливості , де . Загальнопоширеним методом розрахунку таких агрегованих оцінок є зважена сума:

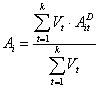.                                                            (1)

Рішення задачі отримують шляхом вибору об’єктів з найкращими значеннями ступенів привабливості до загальної цілі [4].

Необхідно зазначити, що при практичному застосуванні систем нечіткого логічного виводу для розв’язання розглянутого класу задач, саме у випадках залучення до розв’язку задач групи експертів і фахівців з певної предметної галузі, стикаються з суттєвими проблемами, які інколи навіть унеможливлюють використання систем НЛВ в реальних задачах.

Постановка задачі. Розглянемо основні засади системи НЛВ, необхідні для розуміння подальшого матеріалу. Нечіткий логічний вивід визначає відображення вектора вхідних даних в скалярне вихідне значення за допомогою нечітких правил [4,6]. Система НЛВ, як показано на рис. 1, складається з трьох основних компонентів: фазифікатора, механізму логічного виводу та дефазифікатора.

Рис. 1 Загальна схема системи нечіткого логічного виводу

Фазифікатор визначає ступінь належності вхідних значень ,  до нечітких множин входу – лінгвістичних змінних з відповідної лінгвістичної шкали , де – кількість лінгвістичних змінних у шкалі для -того входу, яка, як правило, є рівною для всіх входів. Ця процедура викликана використанням у системі НЛВ лінгвістичних правил, та здійснюється задля визначення ступеню істинності кожної передумови кожного правилу.

Ядром механізму логічного виводу є база правил, яка містить лінгвістичні правила. Ці правила можуть бути задані експертним шляхом, чи отримані із числових статистичних даних. Механізм логічного виводу відображає вхідні нечіткі множини ,  кожного правила у вихідну  з набору вихідних лінгвістичних змінних . Відмінною рисою НЛВ є те, що порядок виконання правил не впливає на результат – правила виконуються паралельно. Правила в базі правил ,  містяться у наступному форматі [4,6]:

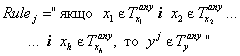                                              (2)

Потім, вихідні нечіткі множини  кожного правила об’єднуються в одну нечітку множину виводу .

Дефазифікатор відображає нечітку множину виводу  у чітке число , яке і є результатом системи НЛВ для заданих вхідних значень , . Тобто діапазон вихідних значень дефазифікатор перетворює в одне числове значення зручне для подальшого використання. На практиці користуються наступними поширеними методами дефазифікації [4]: центроїдний, методи максимуму, метод центру максимумів, висотна дефазифікація.

Зазначимо, що при потужних перевагах системи НЛВ мають суттєвий недолік, який полягає у великій трудо- та ресурсномісткості побудови бази правил.

Оскільки кожен член з комітету ОПР може мати своє переконання щодо важливості того чи іншого критерію, то для підвищення якості рішення доцільно для кожної ОПР  при відпрацюванні циклів системи НЛВ використовувати індивідуальні думки ОПР щодо рівню важливості оцінок за критеріями.

Структура правил нечіткого логічного виводу, побудованих в загальному випадку за (2), зумовлює урахування важливості критеріїв в самих правилах, тобто причинно-наслідкові зв’язки між входами та виходом, які сформульовані в тому чи іншому правилі, за своїм змістом та суттю визначають залежність величини виходу від вхідних значень та взаємного відносного рівню важливості вхідних значень. Тому для урахування індивідуальних переваг кожної ОПР  щодо рівню важливості оцінок за критеріями найбільш коректним постає створення та використання індивідуальних баз правил для кожної ОПР  [7].

Однак, цілком зрозуміло, що такий підхід використання індивідуальних баз правил для кожної ОПР в реальних задачах прийняття рішень є дуже дорогим, трудо- та ресурсномістким, що зумовлює його неприйнятність для практичного застосування – в цьому і полягають зазначені вище проблеми практичного використання систем НЛВ в задачах вибору комітетом експертів [7].

Необхідно розробити підхід застосування системи нечіткого логічного виводу придатний для практичного застосування у реальних практичних задачах із залученням комітетів експертів.

Результати. Пропонується комітету ОПР використовувати систему НЛВ з єдиною базою правил – систему нечіткого логічного виводу із зваженою істинністю [8].

Процес нечіткого логічного виводу у найпоширенішій системі НЛВ за Мамдані [4,6] виглядає наступним чином. База правил ,   складається з правил у вигляді (2). На етапі фазифікації визначаються ступені належності вхідних значень ,  до нечітких множин входу, тобто визначаються ступені істинності  для кожної передумови кожного правила . Далі для кожного правила  на основі ступенів істинності передумов  розраховується ступінь його виконання . Для цього застосовують композицію на основі оператору мінімуму:

        ,  .                               (3)

І для кожного правила на основі ступеню виконання ,  розраховується результат його виконання – вихідна нечітка множина з усіченою функцією належності . Визначення усіченої функції належності, тобто операція імплікації, також відбувається за допомогою оператору мінімуму:

       ,  .                                          (4)

Наприкінці механізму логічного виводу вихідні нечіткі множини виконаних правил за допомогою оператору максимуму агрегуються в нечітку множину виводу , функція належності якої має наступний вигляд:

.                                          (5)

Нечіткий логічний вивід Мамдані для системи НЛВ з двома входами та двома виконаними правилами графічно проілюстровано на рис. 2.

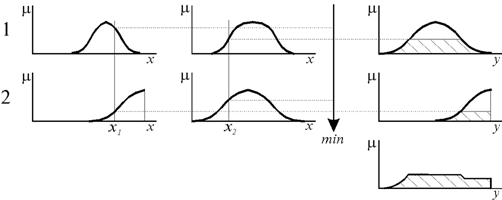
Рис. 2 Ілюстрація нечіткого логічного виводу Мамдані

На останньому етапі приведення до чіткості для знаходження остаточного результату  вдаються до процедури дефазифікації нечіткої множини [4]. Метод дефазифікації обирається в залежності від конкретної задачі. Придатними для запропонованого методу агрегації значень в задачах прийняття рішень постають наведені вище методи дефазифікації: центроїдний, методи максимуму, метод центру максимумів, висотна дефазифікація.

Центроїдний метод (рис. 3) полягає у знаходженні центру ваги (центроїду) нечіткої множини , який і обирається за результат :

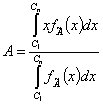.                                                              (6)

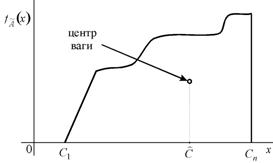
Рис.3 Дефазифікація центроїдним методом

Методи максимуму, які графічно показані на рис. 4, полягають у виборі чіткого результату  серед тих значень, для яких значення функції належності , тобто ступінь належності є найбільшим. Серед методів максимуму найпоширеніші: метод першого максимуму та метод середнього максимуму.

У методі першого максимуму чітке значення  знаходиться як найменше значення, при якому досягається найбільше значення функції належності :

,      тобто  .                              (7)

У методі середнього максимуму чітке значення  знаходиться відповідно як середнє значення з тих, при яких досягається найбільше значення функції належності . Середній максимум на рис. 3 позначений .

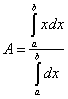.                                                                (8)

У методі центра максимумів виходом  є середня точка між центрами областей значень , при яких функція належності  утворює найвищі «плато». Застосування даного методу графічно зображено на рис. 5.

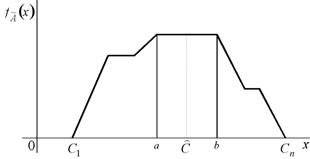
Рис.4 Дефазифікація методами максимумів.

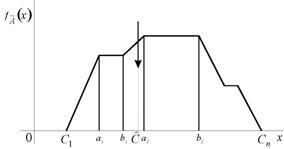
Рис.5 Дефазифікація методом центра максимумів.

            Метод висотної дефазифікації полягає у знаходженні центроїду -рівня, тобто з нечіткої множини  до уваги приймаються лише ті значення , для яких , :

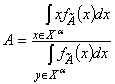,   ,   .                      (9)

При  з методу висотної дефазифікації (9) виходить центроїдний метод (6).

Система нечіткого логічного виводу із зваженою істинністю, що запропонована для використання комітетами експертів, полягає в наступному. Опорна база правил, в такій єдиній системі НЛВ створюється з покладанням рівної важливості ,  для всіх критеріїв , . При застосуванні запропонованої системи НЛВ для кожної ОПР ,  відбувається корегування процесу логічного виводу з урахуванням її індивідуальних значень вагових коефіцієнтів  критеріїв , . Звичайно вагові коефіцієнти  є нормованими, і в таких випадках доцільно б було їх використовувати як корегувальні множники. Тобто в системі НЛВ за таким методом ступінь істинності кожної передумови , що відповідає критерію , правила  для ОПР  помножується на відповідний ваговий коефіцієнт . Тоді за (3) ступінь виконання  правила  при застосуванні системи НЛВ для ОПР  буде визначатись таким чином:

.                          (10)

Однак, у такому разі значення оцінки за менш важливим критерієм, якому відповідає менше значення вагового коефіцієнту, буде спричиняти більший вплив на значення ступеню виконання  правила, тому що у процедурі композиції (4) відповідно до логічного «» використовується оператор мінімуму [8]. Вочевидь, що такий спосіб зважування ступенів істинності передумов правил для даної проблеми не є коректним.

Впровадження зворотних вагових коефіцієнтів  у якості корегувальних множників також не призводить до коректного відображення вагових співвідношень між значеннями оцінок за критеріями у розрахунку значень ступенів виконання правил. Оскільки в такій ситуації найбільший вплив також може спричинити оцінка за менш важливим критерієм (при меншому ступеню істинності передумови за цією оцінкою).

Отже, використання єдиної опорної бази правил системи нечіткого логічного виводу може суттєво поліпшити умови практичного застосування СНЛВ в реальних практичних задачах прийняття рішень із залученням комітетів експертів, проте, це потребує розв’язання зазначеної проблеми коректного корегування єдиної бази правил для кожного члену комітету.

Для адекватного урахування різних значень вагових коефіцієнтів векторів ОПР  та забезпечення участі кожної оцінки у формуванні значення ступенів виконання правил та, відповідно, у результаті логічного виводу при використанні єдиної бази правил пропонується для визначення ступеню виконання  правила в процедурі композиції ступенів істинності передумов правила (3, 10) замість оператору мінімуму використовувати зважену суму значень оцінок, тобто лінійну комбінацію значень оцінок за всіма критеріями та їх вагових коефіцієнтів.

За таким підходом ступінь виконання  правила  при застосуванні системи НЛВ для ОПР  буде визначатись наступним чином:

.                                                      (11)

Тобто, для розглянутої задачі багатокритеріального вибору операція композиції для правила  в процедурі нечіткого логічного виводу системи НЛВ із зваженою істинністю для об’єкту  та ОПР  формулюється так:

.                                               (12)

Зазначимо, що запропонована до використання система нечіткого логічного виводу із зваженою істинністю не є існуючою зваженою системою НЛВ. Ідея зваженої системи НЛВ полягає у тому, що кожному правилу  надається своє значення ваги.

Висновки. Запропоноване використання системи нечіткого логічного виводу із зваженою істинністю забезпечує врахування індивідуальних значень вагових коефіцієнтів критеріїв оцінювання об’єктів для кожної ОПР при застосуванні єдиної бази правил для комітету ОПР, знімає необхідність побудови і використання індивідуальних баз правил для кожної ОПР і робить системи НЛВ практично застосовним засобом в реальних задачах прийняття рішень, а саме в задачах багатокритеріального оцінювання і вибору із залученням комітетів експертів.

Подальший розвиток доцільно проводити у напрямку розробки підходів до спрощення і автоматизації процесу побудови бази правил системи НЛВ як експертним способом, так і з наявних статистичних даних систем, об’єктів, процесів та явищ, що досліджуються.

1.                  Zadeh L.A. Fuzzy Sets // Information and Control. 8(1965), pp.338-353.

2.                  Орлов А.И. / Математические заметки. 1981. Т.30. №4. с.561-568.

3.                  Коршевнюк Л.О., Коршевнюк Д.О., Мінін М.Ю.  Патент 71851 A України, МПК G 06 F 17/60, N 7/06. Спосіб одержання якісних експертних оцінок при моделюванні економічних, соціальних, біологічних систем. – № 20031213217; Заявл. 31.12.2003; Опубл. 15.12.2004, Бюл. “Промислова власність” № 12.

4.                  Коршевнюк Л.А., Бидюк П.И. Решение задачи распределения инвестиций на основе нечеткого логического вывода // Системні дослідження та інформаційні технології. – 2003. – №2. – с.34-42.

5.                  Коршевнюк Л.А., Бидюк П.И. Решение задачи распределения инвестиций между альтернативными проектами // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.Є.Пухова. – Випуск 17. – Київ, 2002. – с.26-33.

6.                  Mamdani E.H. Applications of fuzzy logic to approximate reasoning using linguistic synthesis // IEEE Transanctions on Computers, 1977, v. 26, No. 12, pp. 1182-1191.

7.                  Коршевнюк Л.О., Мінін М.Ю., Бідюк П.І. Підхід групового застосування системи нечіткого логічного виводу // Математичне та програмне забезпечення інтелектуальних систем: Тези доповідей учасників ІI міжнародної науково-практичної конференції. – Дніпропетровськ: ДНУ, 2004. – с.66-67.

8.                  Коршевнюк Л.О., Мінін М.Ю. Система нечіткого логічного виводу із зваженою істинністю // Единое информационное пространство ‘2004: Сборник докладов II-й Международной научно-практической конференции. – Днепропетровск: ИПК ИнКомЦентра УГХТУ, 2004. – с. 114-117.