УДК:681.5+683.3

До настоящего времени невозможно формализовать решение задачи управления процессом кристаллизации сахара в аппарате периодического действия, хотя имеется ряд математических моделей процесса и описаний кинетики кристаллизации сахара [1, 2, 3]. Кроме того, отсутствие технических средств для измерения пересыщения нечистых сахарных растворов еще более усложняет задачу. Такая ответственная стадия как заводка кристаллов до сих пор практически не совершенствуется. Заводка кристаллов с использованием «сахарной пудры» приводит к использованию водных или соковых «расчисток» кристаллов для достижения необходимого количества кристаллов в начальном объеме сиропа. Применение суспензии кристаллов в изопропаноловом или этиловом спирте несколько стабилизирует этот процесс, однако не обеспечивает необходимого количества кристаллов в объеме начального набора аппарата, что также ведет к необходимости водной (соковой) расчистки кристаллов. С целью ввода необходимого количества кристаллов в начальный объем набора сиропа в аппарат и их сохранения разработана твердопластическая паста с размером кристаллов, которые не растворяются при вводе их в аппарат [4]. Пастообразная форма композиции кристаллов позволяет стабильно прогнозировать количество кристаллов в единице массы пасты. Это количество определяется объемом сиропа начального набора аппарата. Паста позволяет более эффективно вести процесс варки утфелей с использованием автомата варки, функционирующего по стадиям: стабилизация объема начального набора аппарата, сгущение до ввода пасты, ввод пасты, «закрепление кристаллов», рост кристаллов с подкачкой сиропа, рост кристаллов с подкачкой белого оттека, отварка утфеля.

Кроме того, переход от стадии к стадии носит «размытый» характер в виду отсутствия точных значений пересыщения раствора. В этих условиях, когда нет уверенности в результатах последействий автомата или оператора, более точным является автомат, построенный на основе метода группового учета аргументов по стадиям процесса.

В качестве модели хода процесса варки утфеля используется сетевой граф (автомат) с размытыми функциями перехода. Этот граф должен соответствовать образу мышления человека-оператора, контролирующего ход процесса при условии, что следующее состояние процесса указывает ребро графа с большей размытой функцией перехода. При условии, когда возможен ряд управляющих воздействий (подкачка раствора или повышение температуры раствора), используют сетевую модель для выбора такого исходного состояния, при котором большая функция перехода приводит в состояние с наименьшей функцией потерь. Генерация эвристик при этом определяет процесс поиска оптимального решения при помощи перебора ходов. При этом сумма вероятностей всех возможных альтернатив не равна единице. Переход из одного состояния в другое определен нечетко, размыто. Для решения задачи ход процесса моделируется по стадиям на основе моделей стадий в виде размытого автомата с функцией членства, заданной на размытом множестве Q × J × Q.

                                                                  (1)

где Q = {q₁, q₂, …, q_n}- алфавит внутренних состояний.

Каждому состоянию соответствует фиксированный набор информации, получаемой от датчиков, установленных на объекте. Среди информации выделяют данные с наивысшим приоритетом (вязкость, электропроводность или температура).

Пусть J = {i₁, i₂, …, i_n}- входной алфавит или алфавит управляющих воздействий,

f - размытая функция перехода, принимающая значения в интервале 0, 1.

Вид размытой функции:

при                                    (2)

q(k +1) = q_m = f ^j_em → [0, 1],

где q_e, q_m  Q - состояние размытого автомата в k-й и k +1 моменты времени.

Для решения задачи перехода введем два порога β и ρ так, чтобы Q < ρ < β <1.

Если f (q_e, i_j, q_m) ≥ β, то q_e → q_m существует при i_j  J.

Если f (q_e, i_j, q_m) ≤ ρ, то перехода не существует.

В основу функционирования модели, построенной на размытом автомате, положена формула Заде о композиции двух отношений, заданных на данном размытом множестве

                                                                            (3)

т. е., чтобы найти композицию двух отношений размытого множества А нужно выбрать минимальную функцию членства между f (x,υ) и  f (υ,y) и найти то значение для υ, для которого выбранная функция членства достигает максимума.

Формулой (3) можно пользоваться, если задана входная последовательность длиной ℓ = 2.

Если число допустимых состояний автомата i₁(k), i₂(k+1), i₃(k+2) определяют последовательность J₃(k) длиной 3, а q_e  и q_s - начальное и конечное состояние автомата, то имеем:

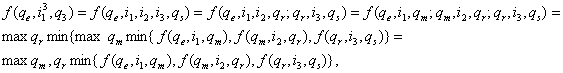       (4)

где m, r = 1, 2, …, n.

Пример: Пусть дан входной алфавит

J₃ = {i₁}, m ∙ c ∙ i₁ (k) = i₁ (k +1) = i₁ (k +2)

и число состояний автомата n = 3 при q₁, q₃ - начальном и конечном состоянии автомата.

Матрица размытого перехода для i₁ имеет вид:

Тогда уравнение (4) преобразуется к виду:

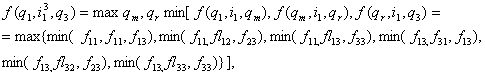                            (5)

где m, r = 1, 2, 3.

Пусть автомат описывается размытым множеством F. Обозначим начальное состояние автомата q_e и конечное - q_s. Разобьем автомат F на ряд подавтоматов F_n, каждый из которых является моделью стадии процесса. Следование подавтоматов F_n соответствует естественному следованию стадий процесса. Каждый подавтомат функционирует на более высоком уровне, чем предыдущий по пути к конечному состоянию. Следовательно, модель многорядная. На каждом ряду конструируется новый подавтомат. Переход из одного состояния в другое из последовательности внутренних состояний подавтоматов Q_n - задается, кроме функций членства f_ij(i, jQ_n), матрицей потерь G_n. При этом на каждом шаге модели определяется последовательность управляющих воздействий из входного алфавита полуавтомата, которая приводит к размытому переходу с наибольшей функцией членства (max f_ij) и наименьшим значением функции потерь (min f_ij) и формируется генерация эвристик вида:

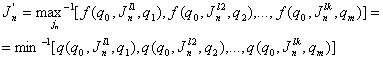                                                      (6)

при q₀, q₁, …, q_m  Q_n,

где       q₀ - начальное состояние подавтомата F_n;

ℓ₁, ℓ₂, …, ℓ_к - длина входной последовательности J_n.

Заполнение матрицы размытого перехода, элементами которой являются размытые функции перехода {f_ij} производятся назначением субъективных вероятностей. Определение функций членства базируется на информации реализуемости перехода, которая определяет знания о переходе. Матрица потерь заполняется с учетом последствий выполнения ряда управляющих воздействий. Таким образом, модель реализует метод группового учета аргументов, т. е. это многорядная система с генерацией комбинаций на каждом ряду с последующим отбором по максимуму функций членства и минимуму функций потерь.

Рассмотрим пример автомата кристаллизации сахара, базирующийся на диффузионно-кинетической модели процесса, предусматривающей в качестве  движущей силы процесса параметры диффузионной кинетики процесса и параметры термокинетической теории процессов.

Автомат варки утфеля имеет ограниченное количество стадий процесса:

- сгущение раствора до заводки кристаллов;

- заводка кристаллов;

- рост кристаллов;

- отварка утфеля.

Исходными данными для моделирования процессов являются:

-  температурный режим в аппарате: T{P₁, P₂, t} - набор измеряемых данных, где P₁ - абсолютное давление греющего пара; P₂ - абсолютное давление в аппарате; t - температура раствора в аппарате;

- уровень раствора в аппарате – h;

- параметр (комплекс параметров), характеризующий свойства раствора C_n, оцениваемый коэффициентом пересыщения α, измеряется косвенным способом по физико-химической температурной депрессии или по электропроводности и вязкости сиропа.

Условия: α = 1,00 - насыщенный раствор сахарозы (кристалл не растет и не растворяется);

1,0 < α ≤ 1,15 - метастабильный раствор (кристаллы сахара растут, новые кристаллы не образуются);

α ≥ 1,2 - лабильное состояние раствора (кристаллы сахара растут, образуются новые кристаллы).

В наборе показаний {T, h, C_n} приоритет в определении состояний и этапов имеет параметр C_n.

Граф модели процесса, состоящей из четырех стадий, приведен на рис. 1 (для случая уваривания утфеля из сиропа при СВ_сир ≤ 65%).

Стадия 1 - сгущение сиропа характеризуется состояниями: q₀ - начальное состояние - ненасыщенный раствор; q₁ - стабильное или метастабильное состояние раствора (1,00 < α ≤ 1,20); q₂ - пересыщенный лабильный раствор ( α = 1,25); q₃ - сильно пересыщенный раствор ( α > 1,25).

Входной алфавит для первого этапа состоит из одного элемента J₁₂ = {i₁}, где i₁ - подача пара в аппарат.

Стадия 2 – кристаллообразование, состояния: q₁, q₂, q₃ - возможные начальные состояния; q₄ - сироп в аппарате с готовыми кристаллами; q₅ - сироп в аппарате с зародившимися кристаллами или с кристаллами пасты затравки.

Входной алфавит для второй стадии состоит из трех элементов J­_II = {i₁, i_2, i₃}, где i₂ - ввод затравки (пудры, или суспензии кристаллов, или пасты); i₃ - подкачка сиропа, закрепление кристаллов (рост до среднего размера 0,3 мм).

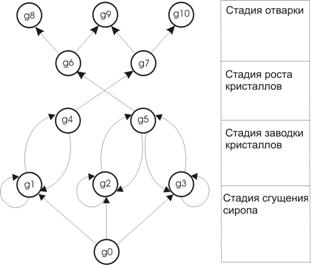
Рис. 1 Сетевой граф хода процесса варки утфеля

Стадия 3 - рост кристаллов, состояния: q₄, q₅ - возможные начальные состояния; q₆ - возможное возникновение вторичных кристаллов; q₇ - кристаллизация без возникновения вторичных кристаллов.

Входной алфавит для третьей стадии варки утфеля: J­_III = {i₁, i_3, i₄}, где i₄ - подкачка белого оттека в аппарат.

Стадия 4 - сгущение утфеля (отварка) до заданного содержания сухих веществ, состояния: q₆, q₇ - возможные начальные состояния; q₈ - сгущенный утфель с неравномерными кристаллами (СВ_у > 92,5%); q₉ - сгущенный утфель с заниженным содержанием сухих веществ (СВ_у = 92,0%); q₁₀ - сгущенный утфель с равномерными кристаллами.

Входной алфавит для четвертой стадии варки утфеля состоит из одного элемента:    J­_IV = {i₁}

Реализация стадий:

Стадия 1. Подавтомат 1.

Граф показан на рис. 2.

На графе первое их двух чисел над стрелкой указывает на значение размытой функции перехода, второе - на потерю при переходе.

Функции членства и потерь переходов даны в таблице 1.

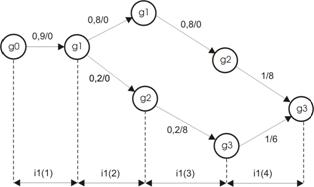
Рис. 2 Граф стадии 1

Таблица 1

Пример заполнения таблицы для к = 3 и перехода в состояния q₂:

f (q₀, i³, q₂) = max{min [ f₀₁, f₁₁, f₁₂], min [ f₀₁, f₁₂, f₂₂] = max{min [0.9, 0.8, 0.8], min [0.9, 0.2, 0.8]} = max{0.8, 0.2} = 0,8

q (q₀, i³, q₂) = max [q (0-1-1-2); q (0-1-2-2) =  max [q₀₁ + q₁₁ + q₁₂ ; q₀₁ + q₁₂ + q₂₂] =

max [6, 6] = 6

Алгоритм функционирования:

1. Максимальна функция членства для k-го момента

f (q₀, i ^k, q_р) = max [ f (q₀, i ^k, q₁), …,  f (q₀, i ^k, q_m)]

2. Проверка f (q₀, i ^k, q_р) ≥ β - «Да» - перейти к пункту 3, «Нет» - перейти к пункту 1 для к+1 момента времени

3. Определить состояние q_р:

q_р = f ^-1(q₀, i ^k, q_р)

4. Найти состояние, переход в которое для к-го момента времени имеет

минимальную потерю

q_сп = min [q (q₀₁, i ^k, q₁), …,  f (q₀, i ^k, q_m)]

5. Сравнить q_р с q_сп.  q_р = q_сп - «Да» - переход к пункту 6;

                                                    «Нет» - переход к пунктам 1, 4 для к + 1 момента времени.

6. Выполнить генерацию эвристик в вербальной форме:

- реализовать управление i ^k, приводящее к переходу в состояние q_р с наибольшим значением размытой функции перехода, но с минимальными потерями.

Алгоритм реализует условие: чтобы довести сгущение сиропа до пересыщенного лабильного состояния (q₂), наиболее благоприятного для образования кристаллов, необходимо остановиться на третьем шаге от начала подачи пара (i₁³).

При этом:

f (q₀, i₁³, q₂) = 0,8 > f (q₀, i₁³, q₃) = 0,2

q (q₀, i₁³, q₂) = 6 < q (q₀, i₁³, q₃) = 8

β = 0,8; k = 5 мин.

Если сделать четвертый шаг, то пересыщение сильно возрастет, кристаллов образуется слишком много. При этом потеря равна:  q (q₀, i ⁴, q₃) = 14.

На первом или втором шаге пересыщение С_n недостаточно, и время образования кристаллов (при заводке „пудрой”) увеличилось бы. При этом

f (q₀, i₁², q₁) = 0,8 > f (q₀, i₁², q₂) = 0,2

При вводе готовых кристаллов с пастой фирмы «Магмас»:

q (q₀, i₁², q₁) = 6 > q (q₀, i₁², q₂) = 0 ,

т. е. наступает реализация пунктов 5, 6 алгоритма функционирования генератора эвристик.

Для остальных стадий процедуры моделирования и синтеза алгоритмов функционирования аналогичны.

Таким образом, предлагаемый подход к решению задач управления процессом на основе моделей стадий процесса варки утфеля решается как в плане выбора управляющих воздействий, так и в плане реализации перехода от стадии к стадии при неполной информации о состоянии объекта.

При групповом учете аргументов данная стохастическая модель управления ходом процесса кристаллизации сахара является более точной, чем другие модели. Реализация управлений в зоне стадий процесса выполняется в системах фирмы ТМА на основе кинетики и динамики, базирующихся на диффузионной теории, молекулярно-кинетической теории с учетом гидратации молекул сахарозы и флуктуационного механизма роста кристаллов.

При этом необходимо перейти на СВЧ-методы контроля пересыщения сахарных растворов или, как минимум, правильно измерять электропроводность и вязкость сахарных растворов, а не сопротивление и момент на валу электродвигателя, как это делают многие фирмы Украины.

Выводы:

1. Предложены стохастическая модель и алгоритмы управления ходом процесса кристаллизации сахара на основе метода группового учета параметров по стадиям процесса, позволяющая осуществлять эффективное управление в соответствии со сложившихся ситуаций.

2. Определены принципы перехода от стадии к стадии при различных состояниях объекта, в том числе и неоптимальных.

1.                  С.М. Петров Кинетическая модель скорости кристаллизации сахарозы из чистых растворов.// Сахар №1 2004 г. с.47-49.

2.                  С.М. Петров Кинетическая модель скорости роста кристаллов сахарозы из чистых и нечистых растворов.// Сахар №6 2004 г. с. 26-29.

3.                  А.А Славянский Моделирование роста кристаллов сахарозы из ее растворов.// Сахар №4 2004 г. с. 37-40.

4.                  А.В. Власенко О применении затравочной пасты «МАГМАС» на сахарных заводах Украины.// Цукор Ураїни №5 2001 г. с. 14-17.

5.                  Д.А. Поспелов Ситуационное управление. –М.: Наука, 1989. 357 с.

6.                  Н.П. Деменков Нечеткое управление в технических системах. –М.: издательство МГТУ им. Баумана, 2005. 199 с.