УДК 681.51
АНАЛИТИЧЕСКАЯ МНОГО РЕЖИМНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ГАЗОВОЗДУШНОГО ТРАКТА БАРАБАННОГО КОТЛА СРЕДНЕЙ МОЩНОСТИ
Ложечников В.Ф., Михайленко В.С., Максименко И.Н.
Повышение экономичности работы теплоэнергетического оборудования за счет повышения технического уровня систем автоматического управления возможно по двум основным направлениям: использование современного комплекса технических средств (компьютеризированные управляющие комплексы с надежными, высокоточными, мало инерционными датчиками технологических параметров) и усовершенствование структурных схем систем автоматического регулирования (как правило, за счет введения в контур контроля дополнительных информационных сигналов об изменении технологических параметров или использование более сложного алгоритма управления [1]).
Большой интерес представляют технические решения, которые без привлечения значительных средств позволяют снизить потребление топлива и уменьшить выбросы вредных веществ в окружающую среду. Исследования, проведенные в США в 1990-1997 годах, показали, что повышение точности регулирования соотношения топливо-воздух позволяет повысить эффективность энергосбережения на 2 - 20%.
На энергетических и промышленных предприятиях Украины в настоящее время идет процесс замены аналоговых систем управления на цифровые. Однако, возможности, которые предоставляют современные технические средства автоматизации, используются не полностью. В частности, на новой технике реализуются типовые схемы и алгоритмы управления, которые были разработаны более 30 лет назад с учетом ограниченных возможностей аналоговых систем управления.
Современный подход к концепции автоматического управления связан с рассмотрением объекта управления в виде сложной динамической системы с определенным числом входов и выходов. Расчет управляющего воздействия происходит с учетом прямых и перекрестных связей между управляющими воздействиями и регулируемыми параметрами. Рассчитанное управляющее воздействие должно обеспечить минимум заданному критерию качества вида
(1)
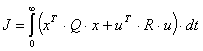
где
![]() – вектор внутреннего состояния объекта
управления;
– вектор внутреннего состояния объекта
управления; ![]() – вектор управляющего воздействия,
– вектор управляющего воздействия, ![]() и
и ![]() –
весовые матрицы.
–
весовые матрицы.
Для решения задачи оптимального управления в соответствии с заданным критерием качества необходима математическая модель, которая адекватно описывает поведение объекта управления во всем диапазоне изменения нагрузок.
Анализ разработанной
математической модели динамики барабанного котла [2] показал, что наряду с
медленно изменяющимися регулируемыми параметрами (давление пара в паропроводе,
солесодержание котловой воды) в объекте управления присутствуют мало инерционные
каналы по разрежению дымовых газов в топочной камере и концентрации кислорода в
уходящих газах. При большой размерности математической модели и большом
численном различии собственных значений матрицы ![]() ,
которое обусловлено сильным различием скорости протекания переходных процессов
в барабанном котле, возникают вычислительные трудности при нахождении матрицы
регулятора системы
,
которое обусловлено сильным различием скорости протекания переходных процессов
в барабанном котле, возникают вычислительные трудности при нахождении матрицы
регулятора системы ![]() . Кроме того, при включении
многомерной системы регулирования все выходы системы должны быть одновременно
замкнуты с ее входами, и, в случае отказа одного из каналов управления или измерения,
а также, переводе части контролируемых параметров на ручное управление, переходные
процессы регулирования в системе могут стать неустойчивым.
. Кроме того, при включении
многомерной системы регулирования все выходы системы должны быть одновременно
замкнуты с ее входами, и, в случае отказа одного из каналов управления или измерения,
а также, переводе части контролируемых параметров на ручное управление, переходные
процессы регулирования в системе могут стать неустойчивым.
Газо-воздушный тракт барабанного котла состоит из газохода и воздуховода. Регулируемыми параметрами для этого участка являются: разрежение дымовых газов в верхней части топочной камеры и избыток воздуха, характеризующий экономичность процесса горения.
При выводе дифференциальных уравнений газохода и воздуховода, как участков регулирования разрежения в топке, были приняты следующие допущения: газоход после дымососа и воздуховод после дутьевого вентилятора очень короткий и что обратная реакция давления в топке на расход мазута и воздуха на входе пренебрежимо мала; аккумулирующая емкость топки и газоходов сосредоточена в одном объеме, а дроселирующая способность газоходов и поверхностей нагрева сосредоточена в одной точке. Регулирование осуществляется путем изменения положения направляющего аппарата дымососа и дутьевого вентилятора. С учетом перечисленных допущений регулируемые участки могут быть заменены упрощенной системой, состоящей из емкости, дросселя и дымососа (дутьевого вентилятора).
(2)
Регулируемой величиной является
отклонение давления в топке
![]() от заданного
значения; входной величиной (регулирующим воздействием) – изменение положения направляющего
аппарата дымососа
от заданного
значения; входной величиной (регулирующим воздействием) – изменение положения направляющего
аппарата дымососа ![]() . В качестве внешнего
возмущения примем изменение расхода уходящих газов на притоке
. В качестве внешнего
возмущения примем изменение расхода уходящих газов на притоке ![]() . Таким образом, дифференциальное уравнение
участка имеет вид:
. Таким образом, дифференциальное уравнение
участка имеет вид:
![]() .
.
(3)
Динамические свойства воздуховода,
определяющие зависимость между изменением подачи воздуха в топку котла и
положением направляющего аппарата дутьевого вентилятора
![]() ,
описываются уравнением вида:
,
описываются уравнением вида:
![]() .
.
Коэффициент избытка воздуха ![]() , который нельзя непосредственно
измерить, может быть определен по содержанию кислорода в дымовых газах
, который нельзя непосредственно
измерить, может быть определен по содержанию кислорода в дымовых газах ![]() практически независимо от состава топлива.
Коэффициент избытка воздуха определяется расходом воздуха
практически независимо от состава топлива.
Коэффициент избытка воздуха определяется расходом воздуха ![]() и расходом топлива
и расходом топлива ![]() . Однако на практике
. Однако на практике ![]() не удается измерить в
точке, расположенной непосредственно за зоной окончания процесса горения. В
большинстве случаев точка отбора пробы находится в конвективной части котла.
При этом газы первоначально перемешиваются в зоне горения, затем
транспортируются через радиационные поверхности и затем дополнительно
перемешиваются в зоне конвективных поверхностей нагрева. Глубокое перемешивание
происходит в дымососе (особенно в дымососах центробежного типа). Во многих
случаях эта сложная при детальном описании схема может быть аппроксимирована
уравнением:
не удается измерить в
точке, расположенной непосредственно за зоной окончания процесса горения. В
большинстве случаев точка отбора пробы находится в конвективной части котла.
При этом газы первоначально перемешиваются в зоне горения, затем
транспортируются через радиационные поверхности и затем дополнительно
перемешиваются в зоне конвективных поверхностей нагрева. Глубокое перемешивание
происходит в дымососе (особенно в дымососах центробежного типа). Во многих
случаях эта сложная при детальном описании схема может быть аппроксимирована
уравнением:
(4)
![]() ;
;
где
![]() – время транспортного запаздывания;
(принимается равным величине инерционности самого газоанализатора).
– время транспортного запаздывания;
(принимается равным величине инерционности самого газоанализатора).
Таким образом, регулируемыми параметрами
газовоздушного тракта барабанного котла являются отклонение от номинального
значения концентрации кислорода в уходящих газах ![]() и
отклонение разрежения в топочной камере, управляющими воздействиями – изменение
положения направляющих аппаратов дутьевого вентилятора
и
отклонение разрежения в топочной камере, управляющими воздействиями – изменение
положения направляющих аппаратов дутьевого вентилятора ![]() и
дымососа
и
дымососа ![]() , возмущающим воздействием – изменение
расхода топлива
, возмущающим воздействием – изменение
расхода топлива ![]() (рис. 1).
(рис. 1).
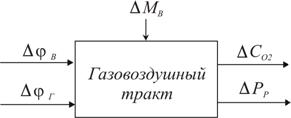
Рис. 1 Параметрическая схема газовоздушного тракта
Численные значения коэффициентов дифференциального уравнения (2) определяются с помощью следующих соотношений:
![]() ;
; 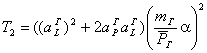 ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
где
![]() – масса дымовых газов в газоходе котла
в стационарном режиме работы, кг;
– масса дымовых газов в газоходе котла
в стационарном режиме работы, кг; ![]() – давление дымовых
газов в верхней части топочной камеры, Па;
– давление дымовых
газов в верхней части топочной камеры, Па; ![]() –
коэффициент (для газа ~0.85),
–
коэффициент (для газа ~0.85), ![]() ,
, ![]() ,
, ![]() –
определяются графически по расходным характеристикам воздуховода и вентилятора
(рис. 2).
–
определяются графически по расходным характеристикам воздуховода и вентилятора
(рис. 2).
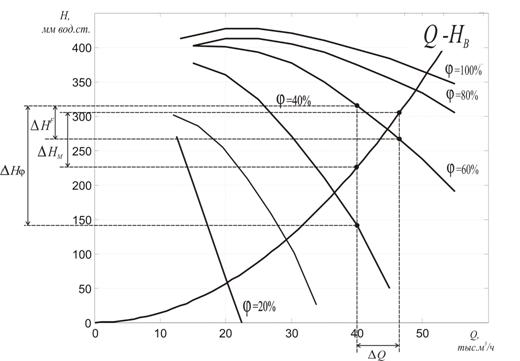
Рис. 2 Напорные характеристики вентилятора и воздуховода
Численные значения коэффициентов дифференциального уравнения (3) определяются с помощью следующих соотношений:
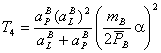 ;
; ![]() ;
; 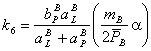 ;
; ![]() ,
,
где
![]() – масса дымовых газов в воздуховоде
котла в стационарном режиме работы, кг;
– масса дымовых газов в воздуховоде
котла в стационарном режиме работы, кг;
![]() – среднее значение давления воздуха в
воздуховоде, Па,
– среднее значение давления воздуха в
воздуховоде, Па, ![]() ,
, ![]() ,
, ![]() – определяются графически по расходным
характеристикам газохода и дымососа (рис. 3).
– определяются графически по расходным
характеристикам газохода и дымососа (рис. 3).
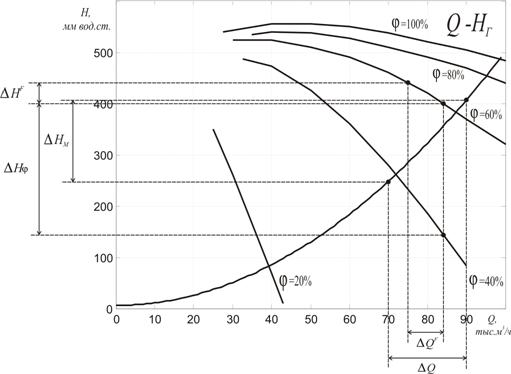
Рис. 3 Напорные характеристики дымососа и газохода
Дифференциальное уравнение, описывающее динамику
изменения концентрации кислорода ![]() в
дымовых газах, параметризуется с помощью следующих соотношений:
в
дымовых газах, параметризуется с помощью следующих соотношений:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
где
![]() ,
, ![]() –
номинальные расходы топлива и воздуха соответственно, кг/с;
–
номинальные расходы топлива и воздуха соответственно, кг/с; ![]() – коэффициент избытка воздуха;
– коэффициент избытка воздуха; ![]() – среднее время прохода дымовых газов
от топки до места замера, с.
– среднее время прохода дымовых газов
от топки до места замера, с.
Поскольку динамические и статические свойства барабанного котла в нестационарных режимах работы являются нелинейными, то для получения многорежимной математической модели, нелинейная модель может быть заменена спектром моделей, линеаризованных относительно нескольких типовых режимов.
Численные значения коэффициентов дифференциальных уравнений (2) ¸ (4) были определены по конструктивным и теплотехническим параметрам газо-мазутного барабанного котла ГМ-50 для трех номинальных режимов, соответствующих 50, 75 и 100% тепловой нагрузки (таблица 1).
Таким образом, многорежимная математическая модель котла, линеаризованная в окрестностях возможных режимов функционирования, может быть представлена системой матричных уравнений
(5)
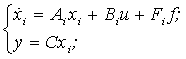
где ![]() – вектор внутренних
состояний, соответствующих i-му режиму функционирования системы;
– вектор внутренних
состояний, соответствующих i-му режиму функционирования системы; ![]() - вектор
контролируемых параметров (выход системы),
- вектор
контролируемых параметров (выход системы), ![]() - вектор управляющих воздействий,
- вектор управляющих воздействий, ![]() - вектор основных возмущений,
- вектор основных возмущений, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - матрицы коэффициентов
соответствующих размерностей. Для обеспечения высокого качества моделирования
процессов во всем диапазоне изменения нагрузок, следует полагать, что матрицы
- матрицы коэффициентов
соответствующих размерностей. Для обеспечения высокого качества моделирования
процессов во всем диапазоне изменения нагрузок, следует полагать, что матрицы
![]() ,
, ![]() ,
, ![]() не являются полностью определенными, а
принадлежат подмножествам
не являются полностью определенными, а
принадлежат подмножествам ![]() ,
, ![]() ,
, ![]() ,
где
,
где ![]() ,
,![]() ,
,![]() - номинальные матрицы подмножеств, а
- номинальные матрицы подмножеств, а ![]() ,
,![]() ,
,![]() - матрицы отклонений,
такие что
- матрицы отклонений,
такие что ![]() ,
, ![]() , i=1..n,
где n – число рассматриваемых режимов функционирования, а матрицы
, i=1..n,
где n – число рассматриваемых режимов функционирования, а матрицы ![]() ,
, ![]() - определяются аналогично.
- определяются аналогично.
Таблица 1
Численные значения коэффициентов модели динамики
газовоздушного тракта котла ГМ-50
|
Паропроизво- дительность, т/ч |
Коэффициент |
||||||
|
с |
с2 |
с |
с2 |
с |
с2 |
|
|
|
25 |
1.67 |
0.0566 |
0.0748 |
3.47∙10-4 |
16 |
56 |
1080 |
|
37.5 |
1.33 |
0.0574 |
0.112 |
8.16∙10-4 |
16 |
56 |
861 |
|
50 |
1.04 |
0.0572 |
0.152 |
7.22∙10-4 |
16 |
56 |
673 |
|
Паропроизво- дительность, т/ч |
Коэффициент |
||||||
|
|
|
|
|
|
|
|
|
|
25 |
80.3 |
-278 |
-20.6 |
0.224 |
4.55∙10-3 |
-39.8 |
2.74 |
|
37.5 |
87.6 |
-254 |
-25.8 |
0.178 |
6.73∙10-3 |
-26.5 |
1.82 |
|
50 |
106 |
-125 |
-19.7 |
0.147 |
6.71∙10-3 |
-19.9 |
1.37 |
Полученная математические модель газовоз душного тракта котла средней мощности (параметризованная для барабанного котла ГМ-50) позволят исследовать возможности применения новых алгоритмов управления, в том числе оптимального многомерного управления. Предпосылкой для применения этого способа управления технологическим процессом является замена на энергетических и промышленных предприятиях Украины аналоговых регуляторов на микропроцессорные управляющие комплексы.
The structure of many-dimensional analytical multiplemode mathematical model and the expressions stating the coefficients of the gas-air tract of average power drum-type boiler is considered. The obtained model can be applied in constructing a modern high-quality computer control system of the boiler.
1. Кокорев С.В., Давыдов Н.И., Анисяев Е.М. Разработка, исследование и испытания системы регулирования разрежения в топке котла-утилизатора комплекса по обезвреживанию и переработке твердых бытовых и биологических отходов // Электрические станции. - 2006. - С. 38-42.
2. Ложечников В.Ф., Стопакевич А.А. Структура многомерной математической модели динамики барабанного котла средней мощности // Оптимизация управления, информационные системы и компьютерные технологии: Труды Украинской академии экономической кибернетики (Южный научный центр). – Киев-Одесса: ИСЦ, 1999. – Вып.1. – Ч.2. – С. 167-176.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.