Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 004.421.6

АЛГОРИТМ ПЕРЕВІРКИ ПРАВИЛЬНОСТІ ГРАНИЦЬ ЗМІНЕННЯ ЗМІННИХ У ПОСЛІДОВНИХ ПРОГРАМАХ

Львов М.С.

Вступ

Комп'ютерні програми, у яких реалізовані розв’язання фізичних задач, мають задовольняти декільком специфічним властивостям. Наведемо деякі із них:

1. Розмірності фізичних величин. Оскільки обчислення в таких програмах засновані на формулах фізичних законів, відповідні змінні, крім ідентифікатора, типу та значення, мають ще одну характеристику – фізичну розмірність. Сучасні мови програмування не використовують за замовчуванням ні типізації змінних за їх фізичним змістом, ні, тим більше, фізичних розмірностей констант і змінних. Тому помилки в програмах, пов'язані з неправильним використанням фізичних розмірностей, не виявляються ні під час компіляції, ні під час виконання програми. Таким чином виникає задача перевірки правильності використання змінних за їх фізичними розмірностями. Цю задачу потрібно вирішувати методами статичного аналізу програмного коду. Користувач має специфікувати всі змінні програми фізичними розмірностями, а аналізатор має перевірити правильність цієї специфікації. Звичайно, аналіз програмного коду має спиратися на співвідношення, які визначені фізичними законами й правилами систем фізичних розмірностей. Наприклад, співвідношення Вольт = Ампер * Секунда - закон Ома в системі СІ.

2. Межі змінення фізичних величин. Результати обчислень, здійснюваних програмою, використовуються в реальних фізичних приладах і пристроях. Тому значення змінних не можуть бути довільними - вони мають перебувати в межах, установлених параметрами приладу або пристрою. Наприклад, у кожному електричному приладі є гранично припустима споживана потужність. Якщо її перевершити, прилад згорить. Помилки в програмах, пов'язані з виходом значень змінних за межі припустимих значень, також не можуть бути виявлені ні під час компіляції, ні під час виконання програми. Цю задачу також потрібно вирішувати методами статичного аналізу програмного коду. Користувач має специфікувати всі змінні програми границями їхніх припустимих значень, а аналізатор має перевірити правильність цієї специфікації.

3. Виконання законів збереження. У фізиці існують фундаментальні закони – так звані закони збереження. Це, наприклад, закон збереження енергії. Можна припустити, що ці закони виражаються співвідношеннями типу рівності між деякими змінними програми. У теорії програмування такі співвідношення називають програмними інваріантами. У правильно написаних програмах інваріанти мають виконуватися у визначених контрольних точках програми незалежно від шляху обчислень і початкових значень змінних. Помилки, допущені у формулах програми, приводять до невиконання цієї умови. Як і у попередніх задачах, помилки такого роду не можуть бути виявлені ні при компіляції, ні під час виконання програми. Задача доведення інваріантності рівності, заданої користувачем у даній контрольній точці програми, вирішується методами статичного аналізу [1-3].

У даній роботі описано алгоритм розв’язання другої з цих практичних задач статичного аналізу програм - задачі перевірки правильності границь змінення змінних у послідовних програмах. Алгоритм використовує базиси Гребнера [4] й методи відділення дійсних коренів поліномів [5].

Постановка задачі

Нехай  - вектор змінних програми  Оператор присвоєння  будемо записувати у виді , де  - деякий алгебраїчний вираз.

                                                             (1)

Послідовною програмою будемо називати послідовність операторів присвоєння

Кожній змінній  припишемо область її визначення – числовий інтервал , , де  - множина раціональних чисел. Через  позначимо декартовий добуток . Для оператора присвоєння (1) через  позначимо числову множину, визначену формулою

.                                                 (2)

            Таким чином, - множина значень змінної – лівої частини оператора (1), якщо вектор - аргумент його правої частини пробігає усю множину визначення вектора змінних  програми.

Насправді ми будемо розглядати оператор присвоєння як оператор, що відображає , причому зміненню піддається тільки -та координата. Отже, можна вважати,  що   Далі, визначимо множину  формулою

                                                (3)

Тепер задачу перевірки правильності границь змінення змінних в програмі можна визначити співвідношенням

                                                                                (4)

Зауваження 1. Насправді  ця задача очевидним чином зводиться до серії задач

                                                                          (5)

Це означає, що її достатньо розв’язати для одного оператора присвоєння (1):

                                                                               (6)

Зауваження 2. У загальній постановці задачу треба було б розглядати для довільних програм, контролюючі діапазони змінення змінних у довільних контрольних точках. Однак, з нашої точки зору, задача у такій постановці є дуже складною і може виявитися навіть алгоритмічно нерозв’язною. Тим не менш, якщо точними методами статичного аналізу буде доведено, що будь-який оператор присвоєння  довільної програми задовольняє умові (5), у довільній контрольній точці програми вектор значень змінних програми буде знаходитися у заданому діапазоні. 

Отже, задачу, яка розв’язується у роботі, можна сформулювати таким чином:

Нехай - функція дійсних змінних . Визначити, чи належить заданому відрізку ?                                                                                                     

Алгоритми, розглянуті нижче, істотно залежать від виду функції . Якщо - поліном, задачу будемо називати визначеною поліноміально. Якщо - раціональна функція, задачу будемо називати визначеною раціонально. Якщо ж формула  містить радикали, задача є радикально визначеною. Ми розглянемо спочатку поліноміально визначені задачі, потім – раціонально визначені задачі, і, нарешті – радикально визначені задачі. Ми будемо також вважати, що коефіцієнти  - суть раціональні числа.

Математичне обґрунтування алгоритму

Задачу ми будемо розв’язувати класичними методами математичного аналізу, використовуючи метод визначення найбільших і найменших значень безперервної функції  на замкнутій обмеженій множині.

1. Метод побудови системи алгебраїчних рівнянь для координат критичних точок відображення. Позначимо через  точку . Нехай у точці  функція   досягає найбільшого (найменшого) значення. Тоді

1.      або

 ,                                                          (7)

2. або точка належить границі паралелепіпеда

Таким чином, алгоритм пошуку критичних та екстремальних точок функції  на множині  може бути заснований на переборі всіх можливих варіантів. Кожний з варіантів визначений підмножиною координат, для яких координатні змінні приймають граничні значення  або . Назвемо такі координати граничними. Для інших координат (назвемо їх внутрішніми) у цьому варіанті потрібно розглядати систему співвідношень (7).  Відзначимо, що загальна кількість варіантів дорівнює .

Будемо вважати, що в даному варіанті необхідні граничні значення змінних уже підставлені в поліном  і результат приведений до канонічного виду. Цей результат ми також будемо позначати через . Покладемо , . (На практиці корисно звільнити поліноми  від квадратів.) Отже,  (7) – система цілих алгебраїчних рівнянь .

2. Метод побудови мінімального полінома для k-ої координати множини критичних точок. Побудуємо базис Гребнера ідеалу , елімінуючи послідовно змінні . Для простоти позначень покладемо . Як відомо [4], базис Гребнера має «трикутний» вид. Запишемо відповідну систему рівнянь:

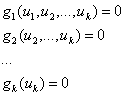                                                   (8)

Система рівнянь (8) рівносильна системі (7), а дійсні корені  рівняння   - суть відповідні координати критичних екстремальних точок .

3. Метод відділення координат критичних точок на відрізку. Ці корені можуть бути відділені на відрізку   з наперед заданою точністю за допомогою, наприклад, алгоритму Штурма [5] (див. Рис.1) 

Рис 1. Відділення коренів

На цьому рисунку позначені корені  й кінці числових відрізків , що відокремлюють ці корені на розглянутому відрізку. (Для простоти в позначеннях опущений індекс .). Для кожного  можна отримати такі відрізки, що . 

Оскільки індекс  може бути обраний довільно, аналогічну процедуру можна застосувати до усіх внутрішніх координат.

4. Метод побудови образів множин критичних точок і кандидатів у критичні точки відображення. Розглянемо множину  точок виду простору , кожна координата яких – дійсний корінь відповідного полінома  на відрізках . Ці точки – суть кандидати в критичні точки полінома  проекції паралелепіпеда  на підпростір, визначений внутрішніми координатами. Пояснимо ситуацію ілюстрацією на графіку для частинного випадку :

Рис 2. Множина точок - кандидатів у критичні точки

Припустимо, що отримана трикутна система рівнянь має вигляд  причому  і усі її корені дійсні. Тоді множину розв’язків системи, оскільки вона є трикутною, можна записати у вигляді  (на рис.2 – чорні точки). У результаті перетворення системи до діагонального виду виключенням  одержимо систему , причому . Тому кандидатами в критичні точки будуть усі пари  На рисунку ми бачимо, що серед кандидатів у критичні точки 4 точки є помилковими. На графіку вони відзначені квадратиками.

Проте, оскільки всі кандидати в критичні точки належать паралелепіпеду , задача  еквівалентна задачам

Розглянемо систему рівнянь

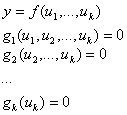                                                   (9)

Елімінуючи послідовно в цій системі змінні  методом побудови базису Гребнера, отримуємо у якості останнього поліном базису  Легко бачити, що серед коренів цього полінома – усі образи множини критичних точок  .

Розглянемо знову систему рівнянь (9). Оскільки ця система зведена до трикутного виду, до неї можна застосувати процедуру діагоналізації, виключаючи недіагональні змінні тим же методом базисів Гребнера. У результаті одержимо систему  

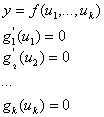                                                        (10)

Елімінуючи послідовно в системі (10) змінні  методом побудови базису Гребнера (як у попередньому випадку), одержуємо як останній поліном базису поліном  Легко бачити, що серед коренів цього поліному – усі кандидати в критичні точки.

5. Метод побудови відповідності «множина критичних точок – образ цієї множини». Проблема полягає в тім, щоб співвіднести кожному елементу множини корінь  числа виду . Розглянемо рис. 3, що ілюструє сказане вище.

Рис. 3. Множина критичних точок та її образ

Апріорі можливі кілька варіантів реалізації співвідношення  Один із цих варіантів показаний на рис.3. чорними кружками, другий – не заштрихованими квадратиками.

1-ий варіант: .

2-ой варіант: .  

У першому варіанті з . У другому варіанті ця властивість не виконується.  

Нехай  і . Тоді

                                         (11)

де  - деякий набір точок з паралелепіпеда з головною діагоналлю . Звідси випливає нерівність

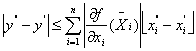                                                   (12)

Значення частинних похідних можна ефективно оцінити через значення границь паралелепіпеда , на якому ми розглядаємо задачу:

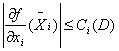
Тому

                                                  (13)

Нерівність (7) ми будемо використовувати для визначення відповідності

                                                      (14)

за наступним алгоритмом. 

6. Основний алгоритм

Нехай  - множина розв’язків системи (4)  і  відповідно точки множини , визначені  у п.3.       

6.1. Відокремимо точки множини паралелепіпедами такими, що , а довжини ребер не перевершують даного додатного числа .

6.2. Відокремимо також точки  множини  відрізками , довжини яких не перевершують даного додатного числа .

6.3. Виберемо в паралелепіпеді точку  з раціональними координатами й обчислимо  Використаємо нерівність (12) для точок у правій частині (12).

                                               (15)

Таким чином, якщо вибрати  , точка  буде відстояти від відділеного кореня  на відстані, меншої за  Проілюструємо описану ситуацію на числовій осі:

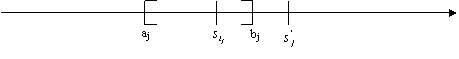
Рис 4. Правило 3-х епсілон

Таким чином, точка має належати відрізку  .

Правило 3-х епсілон

Отже, якщо зафіксувати таке мале додатне число , що при відділенні кореня полінома  відрізки   не будуть перетинатися й не будуть містити кінців відрізка , корені поліномів  потрібно відокремити з точністю .

Тоді визначення відповідності (13) виконується за допомогою основного алгоритму, у якому  обрані за правилом 3-х епсілон.

6.4. Якщо корінь полінома  й точки множини кандидатів у критичні точки відділені з дотриманням правила 3-х епсілон, всі точки  мають належати відрізку . Тоді  належить заданому відрізку. Інакше виконується заперечення цього співвідношення.

Раціонально визначені задачі

У цьому випадку формула функції має вид , , . Якщо границі   скінченні, поліном  на області  не повинен мати дійсних коренів. Таким чином, перший етап алгоритму має відокремити усі корені полінома  таким чином, щоб границі області  не входили до відрізків, що відокремлюють корені.

      Якщо відокремлюючий  паралелепіпед деякого дійсного кореня знаменника  входить до , функція  необмежена на . В іншому разі (другий етап) задача розв’язується цілком аналогічно до поліноміально визначеної задачі, причому у якості поліномів  треба брати поліноми

                                                           (16)

Алгебраїчно визначені задачі

      Для радикально визначених задач формула функції  містить радикали:

. Цей вираз можна перетворити наступним чином:

.

В наших задачах для парних значень  додатково треба врахувати невід’ємність підкореного виразу. Таким чином, для задач над дійсними числами маємо 

Отже, функцію  на області  або на області визначено таким чином:

                                                   (17)

Можна дещо узагальнити (17) вважаючи, що другий кон’юнкт має загальний вид поліноміальної рівності від змінних .

                                                     (18)

Тоді частинні похідні функції  на  обчислюються з формул

()()             (19)

Отже,

()                       (20)

З системи рівнянь (20) можна виключити змінну , побудувавши скорочений базис Гребнера. В результаті отримаємо рівняння , яке грає роль рівняння (7) в алгоритмі розв’язання нашої задачі.   

Висновки

Основний алгоритм, принципи побудови якого описані вище, є досить неефективним. От основні причини неефективності:

1. Перелічення варіантів, що полягає у розгляді всіх - граней -вимірного паралелепіпеду, на якому шукаються найбільші й найменші значення. Як було відзначено у п.1, загальна кількість варіантів дорівнює . Проблема полягає у тому, щоб яким-небудь чином зменшити число цих варіантів.

2. У кожному варіанті будується множина точок – кандидатів у критичні точки. Насправді потрібно знайти тільки дві точки – точку найбільшого максимуму й точку найменшого мінімуму. Для цього досить перебрати множину всіх критичних точок, тобто множину розв’язків системи (9). Однак безпосередньо відокремити точки цієї множини важко. Для цього потрібно було б навчитися відокремлювати корінь по координаті  рівняння виду  за умови, що вже відокремлено корені . Однак аналог методу Штурма для такої постановки задачі нам невідомий. Тому доводиться будувати набагато більшу множину точок, що перебираються - кандидатів у критичні точки.

3. Ще один шлях – поліпшення оцінки (15) залежності  від : у нерівності  константу  потрібно вибрати якомога малою. Тоді зменшиться кількість кроків в алгоритмі відокремлення коренів.

ЛІТЕРАТУРА

1.                  M.S. Lvov. Invariant equalities of small degrees in programs, defined above field // Cybernetics. - 1988. - №1. - P. 108 - 110.

2.                  A.Letichevsky, M.Lvov. Discovery of invariant Equalities in Programs over Data fields. Applicable Algebra in Engineering, Communication and Computing. – 1993. – №4. – pp. 21-29.

3.                  M.Lvov. About one algorithm of program polynomial invariants generation. M. Giese, T. Jebelean. (Eds). Proc. Workshop on Invariant Generation, WING 2007. Technical report no. 07-07 in RISC Report Series, University of Linz, Austria. 06 2007. Workshop Proceedings. pp.85-99 (electronic).

4.                  Б.Бухбергер. Базисы Гребнера. Алгоритмический метод в теории полиномиальных идеалов. В кн.. Компьютерная алгебра. Символьные и алгебраические вычисления: пер. С англ../Под ред. Б.Бухбергера, Дж.Коллинза, Р.Лооса.-М.:Мир, 1986.-392 с., ил. сс. 331-383.

5.                  Дж.Коллинз, Р.Лоос. Вещественные нули полиномов. В кн.. Компьютерная алгебра. Символьные и алгебраические вычисления: пер. С англ../Под ред. Б.Бухбергера, Дж.Коллинза, Р.Лооса.-М.:Мир, 1986.-392 с., ил.  сс. 112-126.