УДК 004.378
нечіткі моделі і методи ідентифікації та прогнозу
стану інформаційної моделі студента
Носов П.С., Косенко Ю.І.
Вступ. Одним з найважливіших завдань професійної освіти є зміцнення зв'язку теоретичних знань з практичними спеціальними уміннями та навичками. Відомо, що кожен суб'єкт навчання оперує образами, складні образи формуються на основі асоціативних зв'язків властивостей раніше сформованих образів, згідно набутому рівню світосприйняття суб'єкта навчання. Спостереження свідчать, що студенти вищих технічних закладів не повною мірою ототожнюють інженерну підготовку зі своєю майбутньою професією. Це можна пояснити недостатньо вираженими зв'язками між інженерними і спеціальними дисциплінами, що ізолюють інженерну підготовку. У зв'язку з цим суттєво знижується не тільки рівень мотивації під час вивчення інженерних дисциплін, але і те, що значний клас понять, що розглядається в інженерних фахових дисциплінах практично не засвоюється.
Актуальність дослідження. Проблема, що склалася, може бути усунена насамперед викладачем, високий рівень педагогічної майстерності якого дозволяє постійно акцентувати увагу на ключових термінах, поняттях, принципах і пов'язувати їх з курсом спеціальної підготовки. Проте у більшості випадків сфокусувати належну увагу студентів на об'єктах вивчення інженерних дисциплін повною мірою не вдається. Таким чином, виникає суперечність між вимогами освітніх стандартів, принципів професійної освіти і дійсним рівнем інженерної підготовки студентів. Необхідність в рішенні позначеної суперечності вказує на актуальність даної проблеми.
Постановка задачі. Не дивлячись на наявні причини такої проблеми, першочергова складність вибору методології її рішення полягає у відсутності класифікації досліджуваних міждисциплінарних і міжоб'єктних зв'язків в рамках певної дисципліни або предметної області (ПрО). Відсутність вагових коефіцієнтів зв'язків, у свою чергу, не дозволяє об'єктивно оцінювати пріоритет відносин об'єктів вивчення. При цьому, відсутність інформаційної моделі студента (ІМС) не дає можливості проводити імітаційне моделювання в різних педагогічних ситуаціях, виконувати прогнозування можливих станів ІМС, що накладає невизначеність на навчальний процес в цілому.
Один з перших підходів рішення задачі класифікації міждисциплінарних зв'язків в даній проблемі був запропонований професором Растрігіним Л.А. і Эренштейном М.Х. [1]. Даний підхід базувався на побудові наближеної моделі знань суб’єкту навчання і адаптації до її властивостей для забезпечення найбільшої адекватності навчального процесу відповідно до індивідуальних когнітивних властивостей. Надалі цей підхід отримав назву – мультилінгвістична адаптивно-навчальна технологія (МЛ-технологія). Вказана технологія ґрунтується на моделюванні пам'яті суб’єкта навчання в навчальному процесі [2]. У МЛ-технології пам'ять суб’єкта навчання представляється у вигляді сукупності певної кількості термінів. Так, при вивченні 1-ої ПрО, внаслідок поетапного поповнення знань, в пам'яті генерується нова множина термінів ![]() і їх значень. При актуалізації i-го терміну в пам'яті виникають асоціації з його значенням:
і їх значень. При актуалізації i-го терміну в пам'яті виникають асоціації з його значенням: ![]() . При вивченні 2-ої ПрО через певний проміжок часу в пам'яті формуються нові значення для нових термінів і правил, множина яких позначена як
. При вивченні 2-ої ПрО через певний проміжок часу в пам'яті формуються нові значення для нових термінів і правил, множина яких позначена як ![]() . Множину значень 2-ої ПрО – KG частково перекриває множина значень 1-ої ПрО – KE, оскільки кількість елементів множини KE в залежності від часу після кінцевого етапу навчання зменшується. Не дивлячись на те, що результатом даного дослідження було знаходження функціональної залежності від часу засвоєння термінів, проте МЛ-технологія не враховує асоціативних зв'язків між термінами в рамках однієї ПрО. Крім того аналізувалися терміни – філологічні синоніми, а не властивості образів.
. Множину значень 2-ої ПрО – KG частково перекриває множина значень 1-ої ПрО – KE, оскільки кількість елементів множини KE в залежності від часу після кінцевого етапу навчання зменшується. Не дивлячись на те, що результатом даного дослідження було знаходження функціональної залежності від часу засвоєння термінів, проте МЛ-технологія не враховує асоціативних зв'язків між термінами в рамках однієї ПрО. Крім того аналізувалися терміни – філологічні синоніми, а не властивості образів.
Результати досліджень. Одним з шляхів знаходження причин певних дій студента – це розгляд ситуації в рамках системного підходу. При цьому, ситуацію необхідно описати з урахуванням проявів попередньої інтелектуальної діяльності студента і визначити функціональні залежності між концептами ПрО – навчальними елементами. Для цього необхідно виконати ряд наступних завдань:
1. Провести класифікацію і індексацію всіх навчальних елементів, в межах дисципліни, що вивчається.
2. Представити навчальні елементи у вигляді складних об'єктів, властивості яких відображаються у відповідних когнітивних властивостях (КВ) [3,4].
3. Визначити зв'язки між результатами рішення практичних завдань і КВ.
4. Визначити залежності зв'язків навчальних елементів у вигляді відносин КВ для окремо взятого студента.
5. Виконати композицію нечітких відносин КВ у вигляді кінцевої нечіткої множини.
6. Виділити класифікуючу нечітку множину професійних компетенцій студента з метою визначення схильності студента до напрямів майбутній професії. З метою наочності, розглянемо послідовність результатів виконання завдань відносно фрагменту інтелектуальної діяльності студента. Припустимо, що студент ініціалізував зв'язки між навчальними елементами відображені на рисунку 1. Композиція нечітких відносин ![]() , наведена у таблиці щодо множини навчальних елементів і тимчасових зрізів знань студента:
, наведена у таблиці щодо множини навчальних елементів і тимчасових зрізів знань студента: ![]() .
.
|
R1° R3 |
q1 |
q2 |
q3 |
q4 |
q5 |
|
1 |
0,3 |
0,6 |
0,4 |
0,6 |
0,2 |
|
2 |
0,3 |
0,3 |
0,3 |
0,2 |
0,2 |
|
3 |
0 |
0,6 |
0 |
0,7 |
0 |
|
4 |
0 |
0,2 |
0 |
0,2 |
0 |
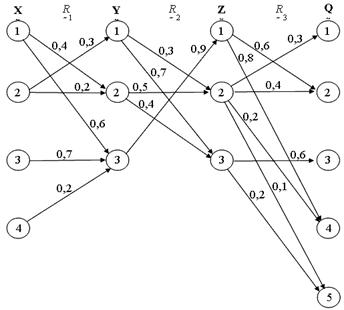
Рис. 1 Нечіткі відносини множини навчальних елементів
Таким чином, за допомогою (min-max) композиції можна відстежити зв'язки між навчальними елементами та їх вагові коефіцієнти. Під час аналізу зв'язків між навчальними елементами, представляється можливість визначити нечіткі відносини КВ конкретного студента у вигляді нечіткого графа. Даний нечіткий граф є апроксимацією бінарного нечіткого відношення K, яке задається на базисній множині КВ і КВ’, ![]() , де
, де ![]() – функція приналежності бінарного нечіткого відношення, яка визначається як відношення
– функція приналежності бінарного нечіткого відношення, яка визначається як відношення ![]() , а через
, а через ![]() позначений кортеж з двох елементів, при цьому
позначений кортеж з двох елементів, при цьому ![]() . Параметри нечіткого графа дають можливість визначити результуючі нечіткі відносини КВ окремого студента. Для цього необхідне декомпозувати кожен КВ щодо графа. Отримані нечіткі множини, проаналізуємо по індексу нечіткості
. Параметри нечіткого графа дають можливість визначити результуючі нечіткі відносини КВ окремого студента. Для цього необхідне декомпозувати кожен КВ щодо графа. Отримані нечіткі множини, проаналізуємо по індексу нечіткості ![]() (1).
(1).
![]() . (1)
. (1)
Дані КВ студента вказують на відносини навчальних елементів інженерних і спеціальних дисциплін, утворюючи тим самим метадані – знання і правила, що визначають особливості моделі поведінки студента в навчальному просторі.
Наступним етапом дослідження є розробка формального апарату експертної системи для порівняння значень отриманих характеристик щодо бази знань професійних компетенцій. При розробці інтелектуальної експертної системи пропонується обрати нечітку модель. Це пов'язано з тим, що основна частина інформації про навчання студента може бути отримана експертним шляхом або у вигляді евристичних описів процесів. Первинний аналіз рівня інженерної підготовки студента може бути представлений декомпозицією підзадач по діагностиці окремих рівнів міждисциплінарних і міжоб'єктних взаємозв'язків.
Кожен такий рівень представляється у вигляді нелінійного об'єкту з множиною вхідних змінних ![]() і однієї вихідної змінної
і однієї вихідної змінної ![]() .
.
Для встановлення залежності між ![]() і у зручніше використовувати якісні терми з наступних терм-множин, заданих на універсальній множині, де
і у зручніше використовувати якісні терми з наступних терм-множин, заданих на універсальній множині, де ![]() - терм-множина змінної
- терм-множина змінної ![]() і
і ![]() - терм-множина змінної у.
- терм-множина змінної у.
Для опису нечіткої бази знань пропонується застосувати алгоритм Мамдані [5] (2).
![]() (2)
(2)
де ![]() - нечіткий терм, яким оцінюється значенням входу
- нечіткий терм, яким оцінюється значенням входу ![]() ,
,
![]() - нечіткий терм вихід, що описує у,
- нечіткий терм вихід, що описує у,
m - кількість термів, використаних для лінгвістичної оцінки вихідних даних,
![]() - ваговий коефіцієнт правил з номером jz.
- ваговий коефіцієнт правил з номером jz.
Алгоритм нечіткого логічного виводу залежить від функції приналежності ![]() входу
входу ![]() нечіткому терму, що представляє процес фаззифікації змінної
нечіткому терму, що представляє процес фаззифікації змінної ![]() :
:
![]() . (3)
. (3)
У свою чергу фаззифікація змінної у, ![]() здійснюється шляхом завдання функції приналежності
здійснюється шляхом завдання функції приналежності ![]() виходу
виходу ![]() нечіткому терму-рішенню
нечіткому терму-рішенню ![]() . Ступінь приналежності
. Ступінь приналежності ![]() нечіткому терму
нечіткому терму ![]() з бази знань визначається системою рівнянь:
з бази знань визначається системою рівнянь: ![]() і визначається як (4):
і визначається як (4):
![]() . (4)
. (4)
Процес дефаззифікації пропонується проводити методом центру ваги для всіх змінних: ![]() .
.
Описана нечітка модель передбачає подальшу оптимізацію із застосуванням навчальної вибірки в конкретних педагогічних ситуаціях, налаштовування моделі може здійснюватися як по структурі, так і по параметрах, залежно від стратегії застосування «м'яких обчислень» і еволюції ІМС. Така еволюція у рамках навчального процесу, передбачає зміну сталих взаємозв'язків навчальних елементів через зовнішні і внутрішні чинники. Через це, важливим етапом аналізу інженерної підготовки майбутніх фахівців – це вчасне виявлення тенденцій зміни зв’язків відносно навчальних елементів. Сигналом зміни таких зв’язків є симптоми, що повторюються, під час неспрацьовування визначених правил. Фіксація сигналів зміни зв’язків дозволяє класифікувати ІМС, визначити її приналежність до конкретної, ціле орієнтованої групи суб'єктів навчання. При цьому множина альтернатив в рамках навчального простору обмежена, оскільки існує максимум навчальних елементів певної інженерної дисципліни.
Враховуючи вищезазначене, представимо задачу знаходження приналежності студента до конкретної, ціле-орієнтованої групи суб'єктів навчання в термінах математичного апарату Парето-оптимальних альтернатив нечіткого відношення переваги.
Хай на універсальній множині альтернатив ![]() задані відносини переваги
задані відносини переваги ![]() , нечіткі з функціями приналежності
, нечіткі з функціями приналежності![]() , а також - вагові коефіцієнти відповідних відносин. Побудуємо згортку відносин
, а також - вагові коефіцієнти відповідних відносин. Побудуємо згортку відносин ![]() у вигляді перетину
у вигляді перетину ![]() , з функцією приналежності (5):
, з функцією приналежності (5):
![]() . (5)
. (5)
Визначимо множину альтернатив що не домінують ![]() на множині
на множині ![]() (6).
(6).
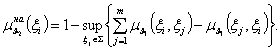 (6)
(6)
Використовуючи згортку критеріїв будуємо нечітке відношення переваги ![]() (7):
(7):
![]() . (7)
. (7)
Знаходимо нечітку підмножину альтернатив що не домінують відносно ![]() (8):
(8):
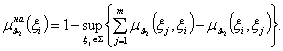 (8)
(8)
Знаходимо перетин множин ![]() та
та ![]() і загальну множину альтернатив що не домінує
і загальну множину альтернатив що не домінує ![]() з функцією приналежності
з функцією приналежності ![]() . Тоді раціональним вважатиметься вибір альтернатив з множини (9).
. Тоді раціональним вважатиметься вибір альтернатив з множини (9).
![]() . (9)
. (9)
Визначивши рівень переваг студента, з'являється можливість у визначенні ймовірності переходу в один з проміжних станів ІМС: ![]() .
.
G0 – аналіз навчального простору;
G1 – вибір стратегії навчання;
G3 – тактика вивчення дисциплін згідно сформованим перевагам ІМС.
Згідно до теореми Колмогорова [6], отримуємо систему рівнянь (10):
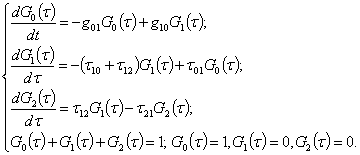 (10)
(10)
Статичним рішенням даної системи рівнянь буде:
![]()
![]() .
.
Таким чином на базі марківських дискретних однорідних ланцюгів з'являється можливість виконати оцінку ймовірності переходу ІМС в нові стани з урахуванням індивідуальних особливостей і інтересів студентів до навчальних дисциплін.
Висновки. У даній роботі розглянуті основні принципи і комбінації застосування математичних моделей спрямованих на вирішення проблеми виявлення зв'язків між інженерними і спеціальними дисциплінами в ході підготовки студентів. Використання моделей спрямоване на формалізацію і упорядковування бази знань ІМС. Застосування експертної системи підтримки прийняття рішень дасть можливість зменшити суб'єктивний вплив на підготовку студентів, а також підвищити інформативність навчального процесу.
ЛІтература
1. Растригин Л.А., Эренштейн М.Х. Адаптивное обучение с моделью обучаемого. – Рига: Знание, 1988.– 160 с.
2. Ковалев И.В., Ступина А.А., Суздалева Е.А. Информационно-алгоритмическое обеспечение мультилингвистической обучающей технологии. Материалы 4-й региональной НМК «Современное образование: массовость и качество». Томск: ТГУСУР. 2001. С. 98–99.
3. Солсо Р. Когнитивная психология. – 6-е изд. – СПб.: Питер, 2006. – 589 с.
4. Носов П.С., Яковенко О.Є, Тонконогий В.М. Використання компонентів мислення експертними системами, як фактору адаптивного впливу в автоматизованих навчальних системах // Тр. Одес. политехн. ун-та. – Одесса: ОНПУ, 2005. – Спецвыпуск. – С. 101–105.
5. Леоненков А.В. Нечеткое моделирование в среде MATHLAB и fuzzyTECH. – СПб.: БХВ-Петербург, 2005.–– 736 с.
6. Портенко Н.И., Скороход А.В., Шуренков В.М. Марковские процессы // Итоги науки и техники. Современные проблемы математики. М. –– ВИНИТИ, 1989. –– 248 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.