УДК 519.651.3

МОДЕЛИРОВАНИЕ ИННОВАЦИОННЫХ РЫНОЧНЫХ СТРАТЕГИЙ

Олейник Ю.Т.

Постановка проблемы в общем виде. Основным фактором успешности функционирования производственно-экономической системы в современных условиях является ее инновационный потенциал, то есть способность системы создавать, тиражировать и использовать новшества [1,2]. Важнейший показатель инновационности результатов деятельности фирмы - масштаб производства качественно новой продукции (доля новшеств в общем объеме выводимых на рынок товаров и услуг). Вывод новшеств на рынок является источником возникновения монополии новатора и стратегическим фактором конкурентного преимущества.

Но вместе с очевидной экономической привлекательностью инновационной стратегии в случае успеха, процесс создания и продвижения на рынок нового товара достаточно дорогостоящий и рискованный. Успех или неудача фирмы, а также уровень риска, связанного с нововведениями, зависят в первую очередь от степени новизны товара и восприимчивости потенциального рынка, то есть стратегических преимуществ новшества, воспринимаемых потребителями (стратегический рыночный риск) [3]. Исследование и прогнозирование влияния этих факторов как на степень конкурентоспособности нового товара, так и на уровень сопутствующего риска - ключевая  и достаточно сложная задача стратегического планирования.

Анализ достижений и публикаций. Выделение нерешенных ранее частей общей проблемы. Решение сформулированной проблемы традиционными методами показало ограниченность возможностей сравнительного статического анализа и моделей конкурентного равновесия в определении зависимости характеристик рыночного положения фирмы от применяемых инновационных стратегий [4]. Выводы экономической теории сводятся к тому, что ориентация на традиционную продукцию и ее незначительные модификации обеспечивает устойчивость равновесного положения фирмы на рынке. Иная ситуация возникает, когда принимается решение о выводе на рынок принципиально новой продукции. Рыночное положение фирмы в этом случае зависит от способности рыночных факторов выбить ее из устойчивого состояния равновесия. Таким образом, традиционный экономический анализ подводит к выводу о состоянии динамической неопределенности системы в случае предложения ею товарных новшеств, но не имеет в своем арсенале инструментария исследования этого явления.

Новое направление в анализе экономических процессов, основанное на использовании методов теории устойчивости и бифуркаций [5,6] для исследования динамики экономических систем в результате нововведений, позволило выявить математические закономерности, на основе которых удалось объяснить известные и получить новые экономические результаты. К последним можно отнести наличие бифуркационной ветви устойчивого развития в области вывода на рынок принципиально новой продукции  и необратимость, гистерезисный характер процесса при изменении инновационной стратегии на противоположную [7,8]. Но результаты нелинейного динамического анализа в основном носят формальный феноменологический характер, вследствие чего закономерно возникает проблема содержательного экономического объяснения выявленных бифуркационных эффектов.

Цель статьи состоит в выявлении и последующем анализе объективно существующей зависимости качественных характеристик рыночного положения фирмы от соотношения предложения и спроса при реализации инновационной стратегии на товарном рынке.

Основной материал исследования. Появление модифицированных или качественно новых товаров ведет, как известно, к неоднородному рынку, который является следствием дифференциации продукта, проводимой предпринимателем. В результате нововведения на рынке начинают действовать эффект замещения и эффект образования спроса [9]. При этом первоначальный базисный спрос на традиционную продукцию и новые базисные спросы на модифицированные и качественно новые товары и услуги могут попарно пересекаться, образуя конкурентные зоны. Хотя базисные спросы могут быть различными, зоны конкуренции являются общими для них, поскольку они представляют собой составляющие двух смежных базисных спросов. Со стороны модифицированной продукции зона конкуренции отражает эффект замещения по отношению к традиционному ассортименту, а со стороны новой – относительно модифицированной продукции. В то же время эффект образования спроса отражается в базисном спросе на модифицированную или новую продукцию соответственно.

Очевидно, что именно причинно-следственные взаимосвязи эффектов образования спроса и замещения с бифуркационными эффектами и возникновением динамической неопределенности определяют качественные характеристики динамики рыночного положения фирмы в процессе реализации инновационной стратегии. В основе решения задачи раскрытия и объяснения этих взаимосвязей лежит выявление и последующий анализ объективно существующей зависимости соотношения предложения и спроса от уровня инновационности поведения фирмы на товарном рынке. Cоотношение предложения новшеств и общего объема выводимых предприятием на рынок товаров и услуг можно характеризовать некоторым параметром . При этом область  соответствует стратегии ориентации на традиционную продукцию и ее модификации, а  определяет область вывода на рынок качественно новых товаров и услуг. Значения  и  отвечают предельным случаям предложения исключительно традиционной либо качественно новой продукции соответственно [6]. Иначе говоря, параметр  является функцией на множестве предложения, оценивающей степень новизны продукции.

Но при конструировании соответствующих аналитических зависимостей возникает проблема неопределенности, связанная с открытостью рыночного взаимодействия фирмы с внешней экономической средой, нечеткостью и динамической неопределенностью взаимосвязей предложения и реакции потребителя. Взаимосвязи в системе "предложение – спрос" не носят дихотомического характера, а отличаются определенной размытостью и не могут быть интерпретированы в терминах "да" или "нет". Нечеткие отношения в системе не позволяют моделировать неизвестные функциональные зависимости, выраженные в виде не столько количественных, сколько качественных связей, классическими математико-экономическими методами теории четких множеств, статистического и функционального анализа. В результате единственной реальной альтернативой является использование в качестве состояний модели нечетких множеств на исходном множестве предложения, а в качестве операторов спроса – нечетких преобразований (отношений) над этими нечеткими множествами.

Базируясь на основных понятиях теории нечетких множеств [10], определим универсальное множество  как множество предложения продукции фирмы со следующей структурой:

где - предложение традиционной, модифицированной и качественно новой продукции соответственно. Входной параметр  определим как функцию принадлежности, отображающую множество  в интервал :

В дальнейшем нечеткое множество  будем отождествлять с его функцией принадлежности . Одним из центральных понятий теории НМ является множество уровня  нечеткого множества , под которым будем понимать четкое подмножество множества , определяемое в виде

Множество уровня  есть образ интервала  при обратном отображении, то есть  Используя понятие множества уровня , можно записать:

все множество предложения

область вывода на рынок модифицированной и качественно новой продукции

область предложения качественно новой продукции

Алгебра над НМ определяется следующими основными операциями:

·        дополнение ;

·        пересечение ;

·        разность .

В соответствии со структурой множества спроса  область значений функции принадлежности  разбивается на два участка - область вывода на рынок модифицированной продукции

и область предложения качественно новых товаров и услуг (5). Граничное значение полной непринадлежности  соответствует области предложения только традиционной продукции:  Область вывода на рынок полностью модифицированной продукции является точкой перехода НМ, для которой

Таким образом, область значений функции принадлежности  можно схематично представить в следующем виде (рис.1):

Рис. 1. Области предложения и значений параметра

Еще более важным фактором, чем степень новизны продукции, является соотношение спроса и предложения, то есть величина востребованности произведенных новшеств (величина инновационного потенциала). В работе [1] показано, что величина инновационного потенциала (востребованность новшеств) может характеризоваться показателем, изменяющимся в интервале . Для моделирования влияния эффектов образования и замещения спроса на устойчивость рыночного положения фирмы определим функцию спроса на  как нечеткое отношение  на НМ :

Согласно введенному определению нечетное отношение (НО)  является нечетким оператором над

Определенный таким образом оператор есть двухместная действительная функция , для которой введем следующие условия:

Все алгебраические операции над НО определяются соответствующими операциями над НМ.

В соответствии с диаграммой предложения (рис.1) в точке перехода НМ теоретически возможны следующие варианты соотношения базисных спросов и образования конкурентных зон (обозначены штриховкой) при изменении параметра  (рис.2):

a)                                                                             б)

в)                                                                             г)

Рис. 2. Схемы развития целевых стратегий предложения: а) и б) – переход от традиционной к модифицированной и качественно новой продукции; в) и г) – обратная стратегия возврата к морально устаревшей продукции

Используя свойства (10) оператора НО и алгебраические операции (7) над НМ, найдем соответствующие выражения для функции спроса по каждой из возможных схем развития инновационной стратегии.

Слева от точки перехода имеем:

для схемы а) -

для схемы б) -  и

В граничной точке  находим  в точке перехода

Справа от точки перехода для схем а) и б) получаем

,   

или        

Во втором случае в точке перехода  а для  имеем

Значения функции спроса для схем в) и г) находятся аналогично. Покажем, что оператор  удовлетворяет неравенству

 для всех

то есть является выпуклым оператором над .

Действительно, если , то

Для  имеем

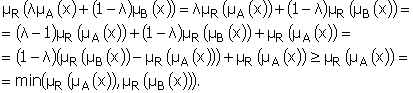
Поскольку функция  является выпуклой, то  - вогнутая функция, возрастающая на  и убывающая на . Поведение функции спроса , соответствующее схемам 2 а)-г), где пунктиром обозначены неустойчивые ветви, представлено на рис.3.

Выводы и перспективы дальнейших исследований. Результаты моделирования стратегии дифференциации продукта с помощью теории нечетких  множеств и нечетких отношений позволяют дать наглядную содержательную экономическую интерпретацию феноменологических бифуркационных  эффектов, выявленных методами теории устойчивости и бифуркаций. Поведение функции нечеткого отношения спроса на нечетком множестве предложения показывает, что источником неустойчивости рыночного положения фирмы является эффект замещения и образования конкурентных зон как следствие стратегии дифференциации продукта, проводимой предпринимателем.

При первичном выводе на рынок модификаций традиционной продукции эффект замещения выражен слабо, базисный спрос на дифференцированный продукт остается неизменным и рыночное положение фирмы устойчиво (рис.3а). Проявление эффекта замещения, приводящее к неустойчивому состоянию системы на множестве традиционной и модифицированной продукции, может иметь место только в случае изменения стратегии дифференциации продукта на противоположную в точке перехода . В этой ситуации происходит падение спроса, возникает гистерезисная петля, система развивается необратимо, переходя на неустойчивую бифуркационную ветвь. При вторичном изменении стратегии развитие системы на множестве традиционной и модифицированной продукции происходит уже по неустойчивой бифуркационной траектории (случай б).

В точке перехода  при выводе на рынок качественно новой продукции возникает бифуркационный эффект, приводящий к смене рыночного положения фирмы на равновесной траектории с устойчивого на неустойчивое при появлении эффекта замещения и образовании конкурентной зоны. При отсутствии ярко выраженной конкурентной зоны падения спроса не происходит и положение системы продолжает оставаться устойчивым на бифуркационной ветви развития (рис.3а).

Схемы в) и г) иллюстрируют поведение функции спроса при обратном изменении стратегии предложения. При обратном переходе через точку  возможны как устойчивый путь изменений ассортимента продукции на равновесной траектории, так и неустойчивое, бифуркационное развитие в результате образования конкурентной зоны и соответствующего падения спроса.

Очевидно, что процесс инновационного развития предприятия носит циклический характер с периодом, равным амплитуде входного параметра :

Переход к следующему циклу формально приводит к переносу начала  координат на фазовой плоскости  "предложение – спрос"  в точку . Цикличность процесса означает, что в случае неустойчивости траектории развития фирмы при выводе на рынок на тот момент качественно новой продукции ее дальнейшая модификация может постепенно вывести фирму в устойчивое рыночное состояние при стратегическом факторе конкурентного преимущества в виде принципиально новой продукции. Такая целевая стратегия в условиях неустойчивости предпочтительнее отказа от вывода на рынок товарных новшеств и перспективы оказаться в формально устойчивом состоянии динамической неопределенности с морально устаревающим ассортиментом предложения.

Рис.3. Графики функции НО спроса  на НМ предложения :

В заключение отметим, что новые экономические реалии нашей страны вызывают необходимость развития перспективных направлений научных, научно-методических и прикладных исследований в области стратегического планирования. Базируясь на использовании современного  математического аппарата и компьютерного моделирования, стратегические инновационные решения могут быть тщательно разработаны, проанализированы и обоснованы с учетом непосредственных и долговременных возможных последствий.

1.                  Плотников А.Н. Оценка инновационного потенциала экономических систем.// Системный анализ в проектировании и управлении. Труды VI-й Междунар. науч.-техн. конф. - СПб.: Изд-во СПбГПУ, 2002.-С.120-124.

2.                  Кононова Е.Ю. Инновационный процесс. Подходы к моделированию.// Модели управления в рыночной экономике. – Донецк: ДонНУ, 2000.-Вып.4.-С.13-18.

3.                  Олейник Ю.Т. Принципы моделирования инновационной стратегии маркетингового менеджмента.// Технічний прогрес та ефективність виробництва. Вісник Національного технічного університету "Харківський політехн. ін-т". –Харків: НТУ "ХПІ; 2001. –С.87-89.

4.                  Занг В.-Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории: Пер. с англ. -М.: Мир, 1999.-335 с.

5.                  Йосс Ж., Джозеф Д. Элементарная теория устойчивости и бифуркаций. Пер. с англ.- М.: Мир, 1983.-301с.

6.                  Баутин Н.Н. Поведение динамических систем вблизи границ области устойчивости.- Изд.2-е, перераб.- М.: Наука, 1984.-176 с.

7.                  Кузнецов В.В., Фирсакова В.В. Об устойчивости рыночного положения фирмы.// Экономика и математические методы.-"Наука", МАИК "Наука/ интерпериодика".-2000.-Т.36, №3.-С.136-139.

8.                  Олейник Ю.Т. Анализ и моделирование стратегий корпоративного менеджмента.// Экономические инновации. – Одесса: Ин-т проблем рынка и экономико-экологических иссл. НАН Украины, 2003. – Вып. 15. –С.190-201.

9.                  Фель У. Оберендер П. Основы микроэкономики: Пер. с нем. – Киев: Укртиппроект, 1997. – 478 с.

10.              Нечеткие множества в моделях управления и искусственного интеллекта/ Аверкин А.Н., Батыршин И.З., Блишун А.Ф. и др.-М.: Наука, 1986. - 312 с.