Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.518.5

ОБНАРУЖЕНИЕ И РАСПОЗНАВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ НА РЕШЕТЧАТОЙ СТРУКТУРЕ

Орлов В.В.

В системах диагностики и идентификации систем широко используется параметрическое описание стационарных случайных процессов на основе ковариационной матрицы или в виде модели авторегрессии (АР-модель) [1,2]. При этом оптимальные алгоритмы обнаружения и распознавания основаны на измерении и преобразовании ковариационной матрицы, что требует большого числа вычислений.

Для анализа спектральных характеристик процессов в настоящее время широко применяются экономичные методы на решетчатых структурах [3], позволяющие перейти от оценивания  параметров ковариационной матрицы к использованию  значений вектора авторегрессии или коэффициентов отражения решетчатой структуры (РС). В тоже время, на базе решетчатых фильтров не решены задачи обнаружения и распознавания процессов, имеющих малый временной интервал стационарности, а также отсутствует анализ их эффективности по вероятностным критериям в случае малого числа выборок. В связи с этим, представляет интерес разработка экономичных подоптимальных алгоритмов принятия решений по множеству выборок на интервале стационарности исследуемого процесса.

В работе проводится разработка и исследование эффективности экономичного по вычислительным затратам алгоритма обнаружения – распознавания на основе анализа параметров случайных процессов.

Для этого предварительно рассматриваются алгоритмы построения для задачи обнаружения нормальных стационарных процессов, а затем исследуется возможности их реализации для распознавания многих классов.

1. Модели входных процессов и параметрические алгоритмы обнаружения.

Пусть входной процесс, представляющий собой аддитивную смесь  выборок помехи  и сигнала , в случае гипотез об отсутствии  и наличии  полезного сигнала имеет вид

; , ,                                                     (1)

которые определяются соответственно ковариационными матрицами размера  помехи , сигнала  и смеси сигнала с помехой

.                                                         (2)

В соответствии с (1)и (2) алгоритм обнаружения сигнала по  исследуемым выборкам заключается в сравнении с порогом решающей статистики, являющейся мерой различия ковариационных матриц входных процессов [4], оцениваемой 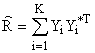 и априорно задаваемой

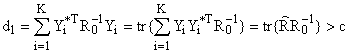,                                         (3)

где  – операция определения следа матрицы;  ,  – векторы размера  исследуемых выборок; – пороговый уровень обнаружителя.

Плотность распределения вероятностей решающей статистики (3) подчиняется  распределению с  степенями свободы, что позволяет легко рассчитать вероятности превышения порога в отсутствии и при наличии сигнала.

            Если входной процесс соответствует модели авторегрессии

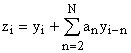,  ,                                                          (4)

где – отсчеты некоррелированного шума, тогда  – коэффициенты авторегрессии (4) связаны с ковариационной матрицей  соотношением

                       (5)

В качестве решающей статистики, по аналогии с (3), используется норма разницы векторов авторегрессии

.                                       (6)

В отличие от первого алгоритма (3), для (6) требуется оценивать не , а лишь  параметров исследуемого процесса, что не только упрощает реализацию, но и должно повысить скорость сходимости алгоритма при ограниченном числе исследуемых выборок.

Если принять оценку параметров авторегрессии как достаточную информацию для принятия решений, то различие параметров известного и наблюдаемого процессов используется для обнаружения, а близость измеренных параметров авторегрессии к одному из классов известных процессов применяется для распознавания классов. Заметим, что процедура оценивания АР-модели -ого порядка связана с необходимостью измерения и обращения ковариационной матрицы исследуемого процесса, в связи с чем требуется вычислительных затрат около  операций умножения и сложения.

Дальнейшее уменьшение вычислений достигается при постоянном интервале дискретизации за счет применения решётчатой структуры, коэффициенты отражения  которой однозначно связаны с АР-параметрами рекуррентными соотношениями Левинсона-Дербина [2]

; ;      ;                            (7)

; ; .

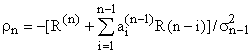 Тогда оценка АР-модели -ого порядка (5) трансформируется в оценку коэффициентов  (7) РС. Существует несколько алгоритмов оценивания в зависимости от априорных сведений о наблюдаемом процессе, стационарности, учета ошибок предсказания и т.п. [2]. Так как обрабатываемые процессы каждой ступени РС порождены одним стационарным процессом, и мощности обоих входов каждого звена РС одинаковы, то представляется целесообразным применение максимально правдоподобных оценок коэффициента корреляции

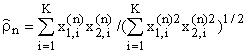,                                           (8)

где  – обрабатываемые процессы на  -ой ступени РС.

            2. Разработка квазиоптимального алгоритма.

Представляет интерес упрощенный алгоритм принятия решения на каждой ступени РС, а затем логическое объединение этих решений. В соответствии с этим положением, при проверке гипотезы  о наличии процесса с коэффициентами отличными от задаваемых коэффициентов помехипротив альтернативы  о его отсутствии определим квазиоптимальный алгоритм обнаружения при пороговых значениях  каждой ступени РС :

–          принимается гипотеза об отсутствии сигнала, если оценки коэффициентов отражения ниже пороговых;

–          принимается гипотеза о наличии сигнала отличительного от априорно задаваемого, если хотя бы на одной из ступеней имеет место существенное различие измеряемых коэффициентов РС от априорно задаваемых

 для всех ;                                                    

 для любого из .                                            (9)

Решающая статистика обнаружителя, реализующего (9), имеет вид

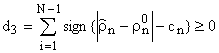,                                                  (10)

где  – единичная функция, отличная от нуля при >1.

Для задачи распознавания принимается решение о наличии  -ого из  классов, если минимизируется решающая статистика

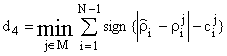.                                                (11)

Структурная схема обнаружителя–распознавателя в соответствии с (10), (11), приведенная на рис.1, реализуется на основе РС, состоящей из  измерителей коэффициентов корреляции, 2 умножителей и 2 сумматоров. Заметим, что при распознавании  процессов достаточно иметь одну решетчатую структуру. Операция обнаружения или распознавания дополнительного класса приводит к добавлению лишь  логических операций сравнения, что не вызывает существенного увеличения вычислительных затрат.

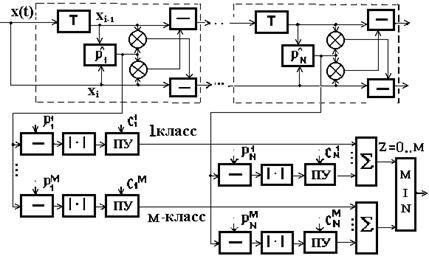
Рис.1 Алгоритм обнаружения-распознавания  классов

3. Анализ эффективности квазиоптимального алгоритма.

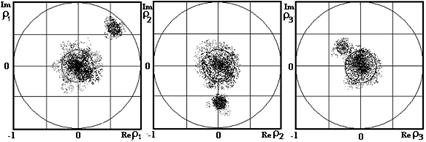
Для выявления особенностей оценок коэффициентов отражения рассмотрим результаты статистического моделирования РС. Исследования проводились на примере двух процессов, один из которых представляется “белым” шумом=0, другой – коррелированным процессом с гауссовой формой спектра и первым коэффициентом корреляции, где =0,9, . Из приведенных значений оценок коэффициентов отражения  первых трех ступеней (Рис.2а, Рис.2б, Рис.2в), полученных при размере выборки =6, видно, что на последующих ступенях происходит сближение кластеров этих процессов, в связи с чем существуют ограничения на выбор РС большого размера. Из анализа Рис.2 следует, что при малом числе выборок, сравнимом с размером РС, использование ступеней >3 не всегда целесообразно.

                                    а)                               б)                                в)        

Рис.2 Ансамбли оценок коэффициентов отражения

Для анализа эффективности адаптации алгоритма в условиях конечного числа обучающих выборок рассмотрим его вероятностные характеристики.

Исследовать распределение решающей статистики (9) можно на основе вероятностных характеристик оценок коэффициентов отражения (8) ступеней РС  и , зависящих от интервала наблюдения . Для случайных процессов, подчиняющихся нормальному закону распределения, в [4] получена плотность вероятностей максимально правдоподобной выборочной оценки (8) коэффициента корреляции

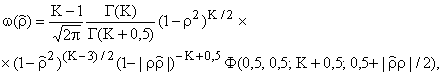        (12)

где  - гипергеометрическая функция.

            Вероятности принятия гипотезы о наличии процесса с заданным коэффициентом отражения  определяется интегрированием плотности (12) в пределах от до . В частном случае, для задачи обнаружения неизвестного коррелированного сигнала на фоне белого шума (Рис.2) априорно задаваемые коэффициенты отражения шума равны нулю, в связи с чем достаточно на каждой ступени РС сравнить с порогом модуль коэффициента корреляции. При этом вероятности ложной тревоги  и правильного обнаружения  каждой -ой ступени РС и результирующие  и  определяются выражениями:

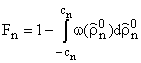
                                       (13)

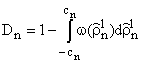
                                                (14)

При необходимости обеспечения равных ложных тревог  на ступенях РС выражения упрощаются

                                                                                 (15)

В случае коррелированной помехи, а также при распознавании процессов, необходимо проводить интегрирование в области . Затем на основе (13-15) определяются ошибки обнаружения и классификации.

            Рассмотрим эффективность обнаружения на примере полезного случайного процесса на фоне мешающего процесса с гауссовыми формами спектров и различающимися первыми коэффициентами корреляции, оцениваемых по выборке малого размера, составляющей  =16 отсчетов исследуемого интервала. На рисунке 3 изображены результаты расчетов вероятностей ошибок и правильных решений.

На Рис.3а приведены зависимости вероятности ложной тревоги от порогового уровня для различных первых коэффициентов корреляции =0..0,65. Анализ графиков показал, что при высоких требованиях к вероятности ошибки , эффективность существенно зависит от корреляционных свойств исследуемого процесса и с уменьшением коррелированности до белого шума вероятность ложной тревоги может возрасти на порядок и более. На Рис.3б представлены зависимости вероятности  правильного решения для случая =2 классов. На входе присутствуют сигналы первого класса в диапазоне первого коэффициента корреляции =0,5 .. 0,75, а отсутствуют сигналы 2-го класса, представленные слабо коррелированной помехой=0,25. Как видно, даже для коротких выборок при различии коэффициентов корреляции на 0,35 и более существуют возможности обнаруживать и распознавать случайные процессы с небольшими интервалами стационарности.

                                                а)                                            б)                                          

Рис.3 Вероятностные характеристики квазиоптимального алгоритма

Заключение

Исследованы взаимосвязи параметров моделей стационарных процессов и рассмотрены соответствующие им алгоритмы обнаружения - распознавания.

Разработан простой обнаружитель – распознаватель на основе решетчатой структуры, требующей  измерителей коэффициентов корреляции,  умножителей и  сумматоров. При распознавании M процессов достаточно иметь одну решетчатую структуру, а для распознавания дополнительного класса достаточно добавление лишь  логических операций сравнения, что не вызывает существенного увеличения вычислительных затрат.

Анализ адаптации предложенного алгоритма показал возможности обеспечивать приемлемые ошибки обнаружения и распознавания для процессов с малым временем стационарности, когда число выборок не менее чем в 4 раза превышает порядок модели авторегрессии.

1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: Пер. с англ. –М.: Мир, 1990. –584 с., илл.

2. Андерсон Т. Введение в многомерный статистический анализ. –М.: Физматгиз, 1963. – 500 стр. с илл.

3. Фридландер Б. Решетчатые фильтры для адаптивной обработки данных // ТИИЭР, т.70, № 8, 1982. –C.54–94.

4. Андерсон Т. Статистический анализ временных рядов. Пер.с англ. –М.: Мир, 1976. – 756с., илл.