УДК 621.372:538.56
МАТЕМАТИЧЕСКИЕ МОДЕЛИ И АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ РЕЛЕВАНТНОСТИ ПРИНИМАЕМЫХ РЕШЕНИЙ С УЧЕТОМ ПСИХОФУНКЦИОНАЛЬНЫХ ХАРАКТЕРИСТИК ПОЛЬЗОВАТЕЛЕЙ ПРИ УПРАВЛЕНИИ АВТОМАТИЗИРОВАННЫМИ ДИНАМИЧЕСКИМИ СИСТЕМАМИ
Передерий В.И., Еременко А.П.
Введение в проблему
В настоящее время в связи с ростом сложности техногенных объектов все более актуальной становится задача создания динамических человеко-машинных систем, использующих интеллектуальные методы управления и принятия решений в режиме реального времени. К числу таких систем относятся: автоматизированные производства, использующие сложные технологические процессы, энергоблоки атомных электростанций, системы транспортных средств и т.д.
Наиболее вероятной причиной выхода динамической автоматизированной системы из строя является человеческий фактор [1]. Значительное внимание уделяется обеспечению комфортной работы пользователя и оптимизации характеристик таких систем, однако практически не рассматриваются вопросы влияния взаимосвязи внешних факторов и психофункциональных характеристик пользователя на принятие релевантных решений в критических ситуациях работы системы [2-4]. С ростом сложности проектирования и эксплуатации человеко-машинных систем появляется необходимость учета данной взаимосвязи, что и обусловливает актуальность данной работы.
Цель работы
Разработка математических моделей и алгоритмов формализации взаимосвязи внешних факторов и психофункциональных характеристик пользователя для определения релевантности принимаемых решений на основе теории нечетких множеств. Создание программных средств автоматизации расчета оптимальных решений при управлении автоматизированными динамическими системами.
Изложение основного материала
Одной из основных характеристик деятельности пользователя автоматизированных систем является релевантность принимаемых им решений. Принятие нерелевантного решения является во многих случаях предпосылкой возникновения аварийной ситуации в системе.
Релевантность решений пользователя зависит от многих факторов. В соответствии с работами [1-3] можно сформулировать следующую классификацию факторов, состоящую из двух групп:
а) факторы, связанные с окружающей средой пользователя;
б) факторы, связанные с текущим состоянием пользователя.
К окружающей среде пользователя автоматизированной системы можно отнести следующие параметры:
а) интенсивность шума ![]() (при превышении порога 120 дБ работа пользователя становится невозможной из-за резкого увеличения времени реакции и невозможности сконцентрировать внимание);
(при превышении порога 120 дБ работа пользователя становится невозможной из-за резкого увеличения времени реакции и невозможности сконцентрировать внимание);
б) интенсивность вибраций ![]() (при превышении амплитуды вибраций порога 0,1 мм становятся значительными утомление и напряженность зрительной системы);
(при превышении амплитуды вибраций порога 0,1 мм становятся значительными утомление и напряженность зрительной системы);
в) освещенность рабочего места ![]() (отклонение освещенности от оптимального для данного вида работ значения, в среднем 1000 лк, приводит к нарастанию напряженности и утомлению пользователя);
(отклонение освещенности от оптимального для данного вида работ значения, в среднем 1000 лк, приводит к нарастанию напряженности и утомлению пользователя);
г) температура ![]() (при превышении порога 33 °С у пользователя ухудшается работоспособность, увеличивается время реакций, возрастает количество ошибок, оптимальным значением температуры является 18...24 °С);
(при превышении порога 33 °С у пользователя ухудшается работоспособность, увеличивается время реакций, возрастает количество ошибок, оптимальным значением температуры является 18...24 °С);
д) влажность ![]() (если влажность превышает уровень 30...60 %, ухудшаются такие психофункциональные характеристики человека, как время реакции, концентрация внимания и др.);
(если влажность превышает уровень 30...60 %, ухудшаются такие психофункциональные характеристики человека, как время реакции, концентрация внимания и др.);
е) давление ![]() (при отклонении от номинального 760 мм рт. ст. наблюдаются ухудшение производительности работы пользователя, увеличение времени реакции, повышение напряженности);
(при отклонении от номинального 760 мм рт. ст. наблюдаются ухудшение производительности работы пользователя, увеличение времени реакции, повышение напряженности);
ж) монотонность работы ![]() (работа, характеризующаяся частым повторением однотипных действий, приводит к быстрому утомлению);
(работа, характеризующаяся частым повторением однотипных действий, приводит к быстрому утомлению);
з) длительность работы пользователя ![]() (существует оптимальное значение длительности работы, в среднем 2...3 ч, при которой производительность пользователя максимальна).
(существует оптимальное значение длительности работы, в среднем 2...3 ч, при которой производительность пользователя максимальна).
В состав группы факторов, связанных с текущим состоянием пользователя входят:
а) ограниченная информационная пропускная способность ![]() ;
;
б) степень утомленности пользователя![]() ;
;
г) ограниченность времени принятия решения ![]() ;
;
д) несоответствие степени напряженности ![]() ;
;
е) недостаточная мотивация ![]() ;
;
ж) недостаточная концентрированность внимания ![]() .
.
Особенностью факторов этой группы является то, что для каждого из них можно определить допустимые пределы изменения или оптимальное значение [2]. Отклонение этой величины от допустимых значений приводит к отрицательным последствиям, в частности, отклонение величины потока информации, поступающей к пользователю, более чем на 50% его пропускной способности, приводит к снижению производительности [3].
Для формализации взаимосвязи факторов и психофункциональных характеристик пользователя (рисунок 1, где (ч) – числовая величина, (нч) – нечисловая величина) целесообразно задать порядковые шкалы и отношения между ними [3, 5].
Пусть некоторая шкала ![]() сформирована и содержит
сформирована и содержит ![]() точек. Тогда ее можно определить как объединение элементов
точек. Тогда ее можно определить как объединение элементов ![]() :
:
![]() (1)
(1)
Пусть заданы две шкалы ![]() , относящиеся к разным величинам:
, относящиеся к разным величинам:
![]() (2)
(2)
![]() . (3)
. (3)
Для описания взаимосвязи между шкалами ![]() и
и ![]() целесообразно использовать бинарное отношение
целесообразно использовать бинарное отношение ![]() , элементы которого характеризуют расстояние между соответствующими точками шкал, тогда отношение является отношением сходства:
, элементы которого характеризуют расстояние между соответствующими точками шкал, тогда отношение является отношением сходства:
 . (4)
. (4)
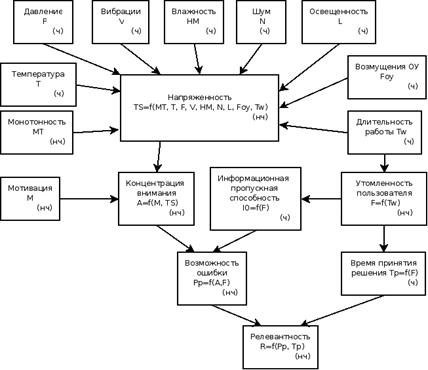
Рис. 1 Взаимосвязь внешних факторов и характеристик пользователей, определяющих релевантность принимаемых решений пользователем.
Для формализации взаимосвязи внешних факторов и психофункциональных характеристик пользователя автоматизированных систем недостаточно задавать величины ![]() равными 0 или 1, поскольку взаимосвязь шкал не является однозначной и строго определенной [1, 3], тогда данную задачу целесообразно решать средствами нечеткой логики, поскольку они предназначены для формализации не полностью определенных величин и качественных понятий [6-8].
равными 0 или 1, поскольку взаимосвязь шкал не является однозначной и строго определенной [1, 3], тогда данную задачу целесообразно решать средствами нечеткой логики, поскольку они предназначены для формализации не полностью определенных величин и качественных понятий [6-8].
Использование математического аппарата теории нечетких множеств позволяет отображать неопределенность значений параметров-шкал ![]() . Если состояние некоторого параметра не может быть отнесено к одной точке его шкалы, его можно представить в виде нечеткого множества:
. Если состояние некоторого параметра не может быть отнесено к одной точке его шкалы, его можно представить в виде нечеткого множества:
![]() (5)
(5)
где ![]() -
-![]() -я точка шкалы параметра
-я точка шкалы параметра ![]() ,
, ![]() - функция принадлежности данной точки, которая показывает степень соответствия рассматриваемой ситуации
- функция принадлежности данной точки, которая показывает степень соответствия рассматриваемой ситуации ![]() -й точке шкалы, знак суммы обозначает не арифметическую операцию сложения, а операцию объединения элементов [9].
-й точке шкалы, знак суммы обозначает не арифметическую операцию сложения, а операцию объединения элементов [9].
Взаимосвязь двух нечетких множеств определяется нечетким отношением, элементы которого представляют собой значения функции принадлежности ![]() для пары элементов множеств
для пары элементов множеств ![]() и
и ![]() :
:
 (6)
(6)
Если известны нечеткое множество ![]() и нечеткое отношение
и нечеткое отношение ![]() , связывающее
, связывающее ![]() и
и ![]() , можно найти нечеткое множество
, можно найти нечеткое множество ![]() с помощью операции max-min композиции: [7]
с помощью операции max-min композиции: [7]
![]() . (7)
. (7)
Если параметр ![]() зависит от других параметров
зависит от других параметров ![]() , то в зависимости от количества параметров
, то в зависимости от количества параметров ![]() можно использовать один из двух способов синтеза модели:
можно использовать один из двух способов синтеза модели:
а) способ частных моделей, в соответствии с которым формируются частные модели:
![]() (8)
(8)
каждая из которых описывает влияние только одного фактора, затем формируется модель агрегирования определяющая совместное воздействие факторов:
![]() . (9)
. (9)
При синтезе каждой частной модели необходимо фиксировать на среднем уровне значение остальных параметров, не входящих в эту модель. Для отображения операции агрегирования может быть использована операция вычисления алгебраической суммы нечетких множеств ![]() , которая определяется как
, которая определяется как ![]() [10]. Способ частных моделей целесообразно применять при
[10]. Способ частных моделей целесообразно применять при ![]() .
.
б) способ общей модели, в соответствии с которым формируется общая модель:
![]() , (10)
, (10)
при этом необходимо анализировать всю область определения такой функции, то есть декартово произведение ![]() . Общая модель представляет собой отношение (6), в котором вместо элементов
. Общая модель представляет собой отношение (6), в котором вместо элементов ![]() используются векторы
используются векторы ![]() где
где ![]() - количество элементов шкалы
- количество элементов шкалы ![]() .
.
Способ частных моделей требует задания меньшего количества точек области определения, однако он характеризуется значительными погрешностями при сильной взаимосвязи между аргументами функции (10). При синтезе частных моделей необходимо правильно выбрать уровни, на которых фиксируются остальные аргументы функции ![]() . Способ общей модели целесообразно применять в случае невозможности разделения влияния аргументов
. Способ общей модели целесообразно применять в случае невозможности разделения влияния аргументов ![]() на величину
на величину ![]() . При этом количество аргументов не должно превышать трех вследствие значительного увеличения количества ячеек таблицы.
. При этом количество аргументов не должно превышать трех вследствие значительного увеличения количества ячеек таблицы.
Применительно к модели взаимосвязи психофункциональных характеристик пользователя автоматизированной системы способ общей модели целесообразно использовать для определения взаимосвязи возможности ошибки, времени принятия решения и релевантности принимаемого решения [3].
Поскольку воздействия окружающей среды пользователя представляют собой числовые величины, то для использования в предлагаемой модели их необходимо предварительно преобразовать в нечеткую форму (фаззифицировать). Методы фаззификации рассмотрены в [10].
Определение размерностей шкал и функций принадлежности нечетких отношений (8) целесообразно производить методом экспертных оценок [11], что позволит обобщить имеющийся у экспертов опыт и знания о влиянии рассмотренных выше факторов на работу автоматизированной системы. Методика обработки экспертных оценок должна учитывать специфику применения нечетких лингвистических переменных, определенных на счетном множестве [3, 7].
Построение формальной модели.
Предположим, что для всех нечисловых величин построены порядковые шкалы, а соответствующие нечеткие значения величин выделим знаком «тильда». Наличие связи между двумя нечисловыми переменными ![]() и
и ![]() обозначим с помощью нечеткого отношения
обозначим с помощью нечеткого отношения ![]() [9]. В качестве операции агрегирования используем алгебраическое суммирование. Система отношений, определяющих взаимодействие между факторами, с учетом обозначений рисунка 1, имеет вид:
[9]. В качестве операции агрегирования используем алгебраическое суммирование. Система отношений, определяющих взаимодействие между факторами, с учетом обозначений рисунка 1, имеет вид:
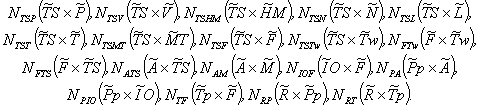 (11)
(11)
Тогда, взаимосвязь между факторами, выразим через следующую систему уравнений:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
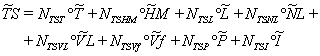 (18)
(18)
Последовательно подставляя выражения (12-18), получим:
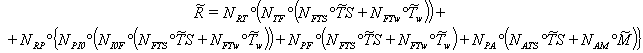
![]()
Данная система уравнений позволяет определить качество принимаемого пользователем решения при известных параметрах окружающей среды, а характеристики пользователя, как звена автоматизированной системы, определяются нечеткими отношениями отображающими связь между характеристиками пользователя и параметрами внешней среды:
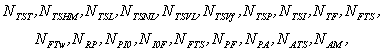
Для расчета оптимальных зависимостей внешних факторов и психофункциональных характеристик пользователя по принятию релевантных решений управления динамическими системами разработано программное обеспечение, позволяющее задавать размерности шкал (рисунок 2), элементы нечетких отношений между шкалами (рисунок 3) и рассчитывать релевантность принимаемых решений с учетом внешних факторов и психофункциональных характеристик пользователя (рисунок 4).
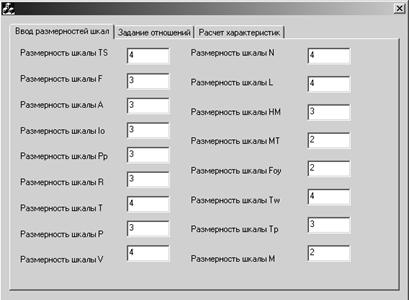
Рис. 2 Интерфейс режима настройки размерностей шкал.
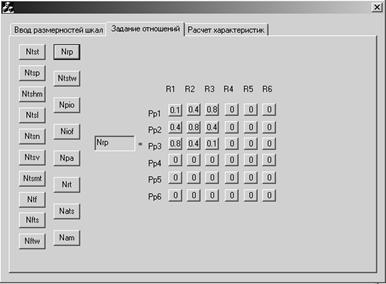
Рис. 3 Интерфейс режима задания отношений
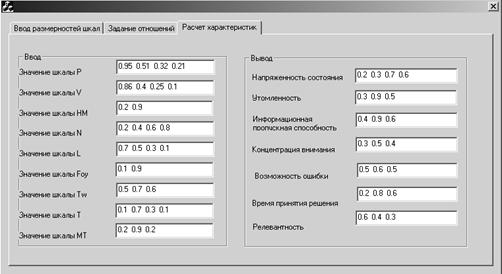
Рис. 4 Интерфейс расчета психофункциональных характеристик пользователя.
Выводы
Разработаны математические модели и алгоритмы формализации взаимосвязи внешних факторов и психофункциональных характеристик пользователя для определения релевантности принимаемых решений на основе теории нечетких множеств.
Для расчета оптимальных зависимостей внешних факторов и психофункциональных характеристик пользователя по принятию решений управления динамическими системами разработано программное обеспечение, позволяющее задавать размерности шкал внешних факторов и психофункциональных характеристик, элементы нечетких отношений между шкалами и рассчитывать релевантность принимаемых решений с учетом перечисленных факторов и характеристик.
Результаты работы могут быть использованы как в учебном процессе по изучению дисциплин принятия решений в управлении динамическими объектами, так и специалистами в области проектирования интеллектуальных систем управления.
Mathematical models and algorithms based on fuzzy sets theory for psycho functional parameters and external factors dependences for determination of users’ decision relevance have been proposed. Specialized software for optimal decision determination for automatic dynamical systems control has been developed.
1. Человеческий фактор. В 6-ти тт. Т. 2 Эргономические основы проектирования производственной среды / Под ред. Г. Салвенди. - М.: Мир, 1991. - 500 с.
2. Ломов Б.Ф. Основы инженерной психологии. Учеб. пособие. Под. ред. Б.Ф. Ломова. - М.: Высшая школа, 1977. - 335 с.
3. Справочник по инженерной психологии / Под ред. Б.Ф. Ломова. - М.: Машиностроение, 1982. - 368 с.
4. Шибанов Г.П. Количественная оценка деятельности человека в системах человек-техника. - М.: Машиностроение, 1983. - 263 с.
5. Орлов А.И. Нечисловая статистика. - М.: МЗ-Пресс, 2004. - 513 с.
6. Kim B.J., Bishu R.B. Uncertainty of human error and fuzzy approach to human reliability analysis // International Journal of Uncertainty, Fuzzyness and Knowledge-Based Systems. v. 14, N. 1 2006, pp. 111-129.
7. Нечеткие множества в моделях управления и искусственного интеллекта / Под. ред. Д.А. Поспелова. - М.: Наука, 1986. - 312 с.
8. Кофман А. Введение в теорию нечетких множеств. - М.: Радио и связь, 1982. - 432 с.
9. Митюшкин Ю.И., Мокин Б.И., Ротштейн О.П. Soft Computing: идентификация закономерностей нечеткими базами знаний. - Винница: Универсум-Винница, 2002. - 145 с.
10. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. - СПб.: БХВ-Петербург. - 736 с.
11. Орлов А.И. Экспертные оценки. Уч. пособие. - М.: МЗ-Пресс, 2002. - 31 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.