УДК 681.327.12.001
СИСТЕМА РАСПОЗНАВАНИЯ ОБРАЗОВ НА БАЗЕ НЕЧЕТКОГО НЕЙРОННОГО КЛАССИФИКАТОРА
Полторак В.П., Дорогой Я.Ю.
Введение в проблему
Теория нечетких множеств оперирует качественными понятиями, что характерно для человека, вместе с тем она дает им количественную оценку, что характерно для ЭВМ. Таким образом, в ней объединяются достоинства человеческого оперирования знаниями и вычислительная мощность ЭВМ. Нечеткая логика, которая служит основой для реализации методов нечеткого управления, более естественно описывает характер человеческого мышления и ход его рассуждений, чем традиционные формальнологические системы. Именно поэтому использование математических средств для представления нечеткой исходной информации позволяет строить модели, которые наиболее адекватно отражают различные аспекты неопределенности, постоянно присутствующей в окружающей нас реальности. Однако при всем своем потенциале теория нечетких множеств не была способна решать практические задачи, а существовала действительно всего лишь как теория. Ситуация изменилась в последние 5-10 лет и это связано с появлением прикладных реализаций для решения интеллектуальных задач с использованием теории нечетких множеств [1].
В статье [2] основоположник теории нечетких множеств Лотфи Заде отмечает тот факт, что появились системы, способные решать такие задачи, как распознавание образов, распознавание речи, распознавание рукописных символов, распознавание голоса, т.е. те задачи, решение которых с помощью компьютерной техники до недавнего времени считалось научной фикцией. На сегодняшний день интеллектуальные компьютерные системы способны идентифицировать отпечатки пальцев, лицевые характеристики, геометрию руки и т.п.
Следует также отметить, что при решении задач с использованием аппарата нечеткой логики аксиомы вводятся по ходу решения задачи и формируются, главным образом, из эмпирических знаний человека.
1. Анализ проблемы и существующих решений
Задача классификации данных (основная задача теории распознавания) в настоящее время является одной из наиболее актуальных сфер приложения систем искусственного интеллекта. Для ее решения было предложено различных подходов и направлений, среди которых наибольшую популярность приобрели решения, сочетающие нейронные сети и нечеткие системы логического вывода. Одним из таких решений является система NEFCLASS (NEuro-Fuzzy CLASSifier) [3, 4, 5], основанная на обобщенной архитектуре нечеткого персептрона. Данная система обладает рядом несомненных достоинств, выделяющих ее среди остальных. Среди наиважнейших следует упомянуть простоту реализации, высокую скорость работы алгоритмов обучения, а также, что является наиболее важным, высокую точность классификации данных - на уровне лучших систем в данной области. Вместе с тем базовая система NEFCLASS имеет ряд недостатков - используемые формулы для обучения параметров носят эмпирический характер, кроме того, неясно, как выбирать в алгоритме обучения параметр скорости обучения а. Цель данной работы – создать альтернативную модель нечеткой нейронной системы.
2. Предлагаемый подход
2.1 Нечеткая фильтрация изображения
Система, выполняющая нечеткую обработку, обладает двумя основными особенностями: во-первых, нечеткий фильтр вычисляет нечеткое приращение таким образом, чтобы оно было менее чувствительно к локальным изменениям структур изображения, таким как границы объектов; во-вторых, функция принадлежности формируется так, чтобы адаптироваться к шумовым составляющим для выполнения нечеткого сглаживания (предполагается, что шум равномерно распределен по всему изображению). Основная идея нечеткого фильтра состоит в следующем: значение пикселя определяется в зависимости от значений окружающих соседних пикселей. Фильтр должен обеспечивать высокую степень различения между шумом и структурными объектами изображения. Чтобы решить данную задачу для каждого пикселя вычисляется оценочная степень, которая характеризирует то, насколько велико или мало приращение в определенном направлении. Конструирование нечеткого фильтра базируется на следующем наблюдении: малое нечеткое приращение соответствует шуму, большое нечеткое приращение - границам объектов. На рис.1 изображен пиксель (x,y) , а также его соседние пиксели NW, N, NE, E, SE, S, SW, W, что соответствует участку изображения размерностью 3х3 пикселя.
|
137 |
94 |
30 |
|
NW |
N |
NE |
|
72 |
15 |
47 |
|
W |
(x,y) |
E |
|
254 |
8 |
92 |
|
SW |
S |
SE |
Рис. 1 Часть участка изображения
Простое приращение центрального пикселя (х,у) в направлении D(D€ {NW,N,NE,E,SE,S,SW,W}) определяется как разность между пикселем с координатами (x,y) и одним из соседних пикселей в направлении D. Значение приращения обозначается ![]() D(x,y) , например:
D(x,y) , например:
![]() N (x,y) = I(x,y-1) – I(x,y) (1)
N (x,y) = I(x,y-1) – I(x,y) (1)
![]() SW (x,y) = I(x-1,y+1) – I(x,y) (2)
SW (x,y) = I(x-1,y+1) – I(x,y) (2)
В основу нечеткого приращения положено следующее наблюдение: если мысленно расположить границу объекта вдоль направления SW-NE через пиксель (x,y), то значение приращения ![]() NW(x,y) будет велико, но также будет велико и значение приращений соседних пикселей, которые перпендикулярны направлению расположения границы объекта, т.е.
NW(x,y) будет велико, но также будет велико и значение приращений соседних пикселей, которые перпендикулярны направлению расположения границы объекта, т.е. ![]() NW(х-1,у+1) и
NW(х-1,у+1) и ![]() NW(х+1,у-1). Идея состоит в том, что если два значения приращений из трех малые, то можно предположить, что в рассматриваемом направлении отсутствуют границы объектов. Таким образом, чтобы определить нечеткое приращение, нужно рассмотреть его качественное понятие малое. Этому понятию в рамках теории нечетких множеств соответствует нечеткое множество малое. Функция принадлежности mk(u) понятия малое может определяться:
NW(х+1,у-1). Идея состоит в том, что если два значения приращений из трех малые, то можно предположить, что в рассматриваемом направлении отсутствуют границы объектов. Таким образом, чтобы определить нечеткое приращение, нужно рассмотреть его качественное понятие малое. Этому понятию в рамках теории нечетких множеств соответствует нечеткое множество малое. Функция принадлежности mk(u) понятия малое может определяться:
mk(u) = 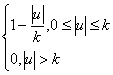 , (3)
, (3)
где к - адаптивный параметр. График выражения построен на рис.2.а.
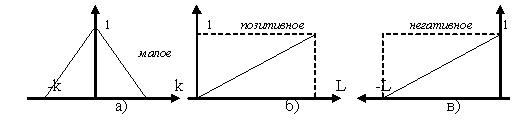
Рис. 2 Функции принадлежности качественных понятий:
а) малое;
б) позитивное;
в) негативное.
Значение нечеткого приращения для пикселя в направлении NW вычисляется при помощи следующих правил:
if (![]() NW(x,y) малое) and (
NW(x,y) малое) and (![]() NW(x-1,y+1)) малое)
NW(x-1,y+1)) малое)
or (![]() NW(x,y) малое) and (
NW(x,y) малое) and (![]() NW(x+1,y-1) малое) (4)
NW(x+1,y-1) малое) (4)
or (![]() NW(x-1,y+1) малое) and (
NW(x-1,y+1) малое) and (![]() NW(x+1,y-1) малое)
NW(x+1,y-1) малое)
then ![]() F NW (x,y) малое
F NW (x,y) малое
Восемь таких нечетких правил применяются для каждого из направлений. Как уже упоминалось ранее, для того, чтобы выполнить нечеткую фильтрацию изображения необходимо устранить шумовые составляющие пикселей путем модификации значений пикселей, поэтому обозначим модификационный параметр difX. Для вычисления значение difX используется пара нечетких правил для каждого направления. Сущность этих правил заключается в следующем: если предполагается отсутствие границ объекта в определенном направлении, то четкое значение приращения в этом направлении может быть использовано для вычисления модификационного значения difX. Следовательно, первая часть функционирования алгоритма фильтрации изображений - выявление границ структурных объектов, может быть реализована в виде нечеткого приращения, вторая часть алгоритма должна быть реализована в виде схемы, которая способна различать позитивное и негативное значение для нечеткого приращения:
![]() : if (
: if (![]() F NW (x,y) малое) and (
F NW (x,y) малое) and (![]() NW(x,y) позитивное)
NW(x,y) позитивное)
then c – позитивное
![]() : if (
: if (![]() F NW (x,y) малое) and (
F NW (x,y) малое) and (![]() NW(x,y) негативное) (5)
NW(x,y) негативное) (5)
then c – негативное
Для описания понятий негативное и позитивное также используются нечеткие множества с функциями принадлежности (рис.2в и 2б).
Последний шаг - дефаззификация результата: необходимо определить модификационное значение difX, которое будет добавлено к текущему значению пикселя:
∆ = ![]() (6)
(6)
где D - обозначает направления, L - количество градаций серого.
Итак, рассмотрен первый этап, который должна выполнять система распознавания образов. Стоит заметить, что этот этап является очень важным, потому как во многом именно от качества предобработанного изображения зависит стабильная работы системы в целом. Следующий этап связан с сегментацией и выделением контуров объектов. Цель этапа - нахождение объекта на изображении.
2.2 Сегментация и выделение контуров объектов
Рассматриваемая нечеткая нейросистема сегментации изображения в работе [6] является самообучаемой. Системы, выполняющие нечеткую сегментацию (кластеризацию) обладают одним существенным недостатком: количество кластеров, как правило, задается человеком.
Описываемая система состоит из многослойного персептрона, который выполняет сегментацию изображения путем выделения адаптивных порогов, используя нечеткие метки [6]. Выход сети описывается как нечеткое множество, а нечеткая энтропия - как функция ошибки процесса сегментации.
Процесс сегментации - это процесс, при котором происходит разбиение изображения на составляющие объекты. При этом обычно используется следующее формальное определение: Пусть F - это обозначение сетки всех пикселей изображения, т.е. набор всех пар: FMxN = {(i,j)}: i = 1,2, ...N; j = 1,2, ...M. При этом ![]() Fi = F, Fi
Fi = F, Fi ![]() Fj = 0, i≠j.
Fj = 0, i≠j.
Фаззификация входного изображения выполняется с использованием значений пикселей. Так изображение в шкале серого может рассматриваться как нечеткое разделение на определенные наборы или классы качественных понятий, как показано на рис.3.
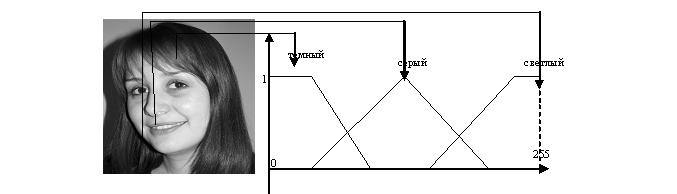
Рис. 3 Функции принадлежности, базируемые на пиксельных значениях
Как уже отмечалось, система сегментации состоит из многослойного персептрона, который выполняет адаптивную многоуровневую сегментацию, используя метки, полученные с помощью метода нечеткой кластеризации. Используется обучение без учителя, т.е. сеть учиться находить признаки классового обобщения во входной информации. Выход нейронной сети описывается нечетким распределением, в то время как нечеткая энтропия выступает в качестве меры ошибки. Описание рационально рассматривать с позиции этапов функционирования системы:
§ формирование гистограммы входного изображения. Данный этап выполняет подсчет количества пикселей с определенными интенсивностями.
§ применение FCM алгоритма. Используется для нахождения нечетких меток [7].
§ кластерная валидация. Здесь основным элементом выступает самоорганизующая нейронная сеть. На вход нейронной сети поступает нормализованная информация в диапазоне [0,1], которая пропорциональна величине интенсивности пикселя. Выходы каждого нейрона имеют значение в диапазоне [0,1]. При обучении на каждой итерации вычисляется ошибка, которая используется для обновления весов. Обучение продолжается до тех пор, пока не будет достигнута минимальная ошибка, или не будет достигнута максимальная итерация обучения. Выходом системы на данном этапе будет набор сегментированных изображений, т.е сегменты изображения лица (для нас важным сегментом является только сегмент глаз).
§ определение функции ошибки. Цель этого этапа - обеспечить определение целевой функции ошибки. В начале происходит фаззификация входного изображения, а затем функция ошибки вычисляется путем определения распределения уровня каждого серого оттенка по отношению к нечеткой энтропии.
§ адаптивное выделение порогов. Этот этап состоит из самой системы выделения порогов, блока вычисления нечеткой энтропии, а также алгоритмa обучения/корректировки. Адаптивное выделение порогов основано на самоорганизовывающейся нейронной сети. Сеть состоит из входного слоя, скрытого и выходного слоев. Каждый слой состоит из MxN нейронов, каждый нейрон соответствует пикселю изображения, причем каждый нейрон слоя соединен только с соответствующим нейроном предыдущего слоя, а также с нейронами со степенью соседства d. Между нейронами одного и того же слоя связь отсутствует. Веса нейронной сети не могут быть инициализированы случайным числом, все они устанавливаются в 1. Для того, чтобы обеспечить более двух стабильных состояний на выходе нейрона разработана специальная функция активации. Эта функция состоит из набора сигмоподобных функций с множественными уровнями. Мультисигмоида образуется путем суперпозиций сдвинутых сигмоидальных функций. Она выражается следующим образом:
![]() , (7)
, (7)
где u – шаговая функция, θk – пороги, yk – целевой уровень каждой сигмоиды, θ0 – параметр крутизны, d – степень соседства, а – параметр активности соседства. Пороги и целевые величины выводятся из функции ошибки. Так как диапазон значений состояния нейронов входного слоя зависит от количества нейронов последующего слоя, то значения порогов адаптированы таким образом, чтобы отображать эту зависимость. Функция ошибки, обозначенная на первом этапе, вычисляется для определения значения выхода на каждой эпохе обучения.
§ дефаззификация. Нейронная сеть работает с интенсивностями пикселей, а не с нечеткими значениями функции принадлежности, как это следовало бы понимать из описания нейронной сети. Другими словами сеть не изменяет значения нечеткой принадлежности пикселей для того, чтобы уменьшить ошибку, а вместо этого она отображает первоначальные значения пикселей на такие значения, которые уменьшают среднее количество нечеткости в соответствии с первоначальным распределением. Таким образом, выход нейронной сети первоначально рассматривается в терминах серого цвета, который далее преобразуется в нечеткость для определения ошибки. Информация о значениях принадлежности пикселей может быть полезна в дальнейшем в зависимости от назначения приложения.
2.3 Нечеткая классификация
В работе [8] представлен новый метод нечеткого распознавания 2-D объектов. Предполагается, что распознаваемый объект корректно позиционирован по отношению к координатным осям, т.е. прошел нормализацию.
Задача распознавания может быть рассмотрена так: предположим, что существует проблема распознавания С - классов объектов в 2-D пространстве. Каждый класс состоит из экземпляров, которые представляют этот класс. В начале необходимо описать экземпляры класса в виде нечеткого представления. Затем для каждого класса с, с = 1...С строится нечеткая модель класса с. Когда неизвестный объект (человек) u должен быть распознан, то сравнивается нечеткое представление u с каждой нечеткой моделью с путем определения меры схожести. Неизвестный объект считается распознанным в том случае, когда он принадлежит классу с наивысшей мерой схожести. Для каждого экземпляра объекта i определяется ограничивающая маска (например, минимальный прямоугольник или овал), которая параллельна координатным осям и содержит экземпляр i, что обеспечивает нормализацию. Пусть горизонтальное и вертикальное пространства обозначаются горизонтальным и вертикальным измерениями ограничивающей маски, содержащей экземпляр i соответственно. Экземпляры объекта класса моделируются путем выполнения следующих шагов:
1) нечеткое разделение горизонтального и вертикального пространств. Деление горизонтального и вертикального пространства на T и K интервалов (Т≠К) выполняется с помощью генетических алгоритмов. Значения T и K, а также размер интервалов оптимизируются таким образом, чтобы выделить те регионы объекта, которые наиболее важны для нечеткого моделирования этого же объекта. Для обоих пространств строится функция принадлежности треугольной формы для каждого интервального экстремума, который является модальным значением нечеткого множества (т.е. значение функции принадлежности в данной точке равняется единице). Каждая функция принадлежности охватывает два соседних интервала, исключением лишь являются первый и последний интервал каждого пространства, для которых функция принадлежности сугубо своя. Метка назначается для каждого нечеткого множества. Распределение точки объекта p = (hp,vp), используемое для конструкционной модели объекта, обладает тем большим значением, чем ближе координата hp к модальному значению нечеткого множества. Следовательно, модальные значения должны выбираться таким образом, чтобы подчеркивать важные величины точек объекта, которые определяются на основании близости координат этих точек к модальным значениям.
Поэтому количество и расположение модальных значений должно быть оптимизировано так, чтобы они действительно отображали ключевые характеристики объекта.
В офтольмогеометрическом методе[9] используется 8 характеристических точек. Для нечеткой модели значение функции принадлежности в этих точках равна 1 (см. рис. 4).
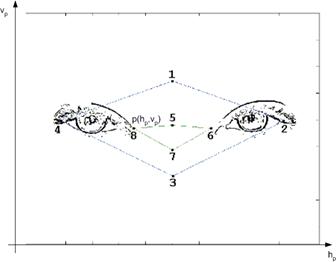
Рис. 4 Определение нечетких меток для офтольмогеометрического подхода
2) нечеткое представление. Для каждого нечеткого множества Vk, k = 1...K+1 ассоциируется горизонтальное значение важности hvi,t,k c каждым регионом Rt,k, t = 1...T+1:
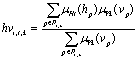 , (8)
, (8)
где Pt,k - это набор точек экземпляра i объекта, который содержится в Rt,k, hp и vp - горизонтальная и вертикальная координаты p-ой точки, μHt и μVk - треугольные функции принадлежности. Рационалое зерно для этого вычисления состоит в том, что распределение hvi,t,k точки, близкой к модальному значению горизонтального и вертикального пространств должно быть больше, чем распределение точки с меньшей степенью принадлежности. Горизонтальное значение важности hvi,t,k лежит в интервале [0,1]. Точно также для каждого нечеткого множества Ht , t = 1...T+1, мы ассоциируем вертикальное значение важности vvi,t,k c каждым регионом Rt,k, k = 1... K+1:
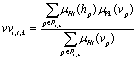 , (9)
, (9)
Вертикальное значение важности vvi,t,k лежит в интервале [0,1].
Для каждого нечеткого множества Vk определяется нечеткое множество Хi,k = {hvi,1,k/H1 + ... + hvi,T+1,k/HT+1} в пространстве меток Ht. Горизонтальное значение важности hvi,t,k является степенью принадлежности к этому пространству. Аналогично для каждого нечеткого множества Ht определяется нечеткое множество Yi,k = {vvi,1,k/H1 + ... + vvi,T+1,k/HT+1} в пространстве меток Vk. Вертикальное значение важности vvi,t,k является степенью принадлежности к этому пространству. Нечеткое представление экземпляра объекта выражается четким множеством Ii = {HIi,VIi}, где четкие множества HIi = {Хi,1,…Xi,K+1} и VIi = {Yi,1,…Yi,T+1} являются горизонтальным и вертикальным нечетким представлением экземпляра. Для каждого класса с, с = 1...С строится нечеткая модель, называемая нечетким представлением класса. Нечеткое представление класса формируется из набора экземпляров класса (обучающего набора). Размер пространства объекта выбирается так, чтобы он соответствовал минимальной ограничивающей маске, как это следует из вышеизложенной информации. Горизонтальное и вертикальное пространства всех экземпляров делятся на Т и К интервалов. Внутри каждого пространства интервалы могут иметь различный размер. Оптимальное количество и расположение интервальных экстремумов в горизонтальном и вертикальном пространствах являются параметрами, зависящими от приложения.
Предположим, что для каждого класса с, обучающий набор состоит из N экземпляров. Для каждого класса с и для каждого нечеткого множества Vk, k = 1...K+1 горизонтальная нечеткая полоса ![]() класса с определяется следующим образом:
класса с определяется следующим образом:
![]() , (10)
, (10)
где ![]() vc,1,k, t = 1...T+1- это средняя величина горизонтального значения важности, ассоциированного с регионом Rt,k. Аналогично для каждого класса с и нечеткого множества Ht, t = 1...K+1 вертикальная нечеткая полоса
vc,1,k, t = 1...T+1- это средняя величина горизонтального значения важности, ассоциированного с регионом Rt,k. Аналогично для каждого класса с и нечеткого множества Ht, t = 1...K+1 вертикальная нечеткая полоса ![]() класса с определяется следующим образом:
класса с определяется следующим образом:
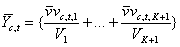 , (11)
, (11)
где 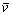 vc,t,k, k =1..K+1 – средняя величина вертикального значения важности, ассоциированного с регионом Rt,k. Следовательно, нечеткое представление класса с есть четкое множество Сс = {HCc,VCc}, где НСс = {
vc,t,k, k =1..K+1 – средняя величина вертикального значения важности, ассоциированного с регионом Rt,k. Следовательно, нечеткое представление класса с есть четкое множество Сс = {HCc,VCc}, где НСс = {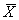 c,1,…
c,1,… 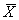 c,K+1} – горизонтальное нечеткое представление класса с, VСс = {
c,K+1} – горизонтальное нечеткое представление класса с, VСс = {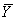 c,1,…
c,1,… 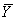 c,T+1} – вертикальное нечеткое представление класса с.
c,T+1} – вертикальное нечеткое представление класса с.
3) Распознавание. Нечеткие представления классов Сс, построенные в фазе обучения, используются для классификации неизвестных объектов. Когда поступает неидентифицированный объект u для выполнения классификации, то вычисляется его нечеткое представление Iu. Затем Iu сравнивается с каждым нечетким представлением класса Сс для определения коэффициента схожести Sc. Для каждого класса с вычисляется коэффициент схожести Sc(Iu,Cc) между нечетким представлением экземпляра Iu и нечетким представлением каждого из классов Сс:
Sc(Iu,Cc) = w1S(HIu, HCc) + w2S(VIu, VCc) (12)
где S(HIu, HCc) - коэффициент схожести между горизонтальным нечетким представлением HIu и HCc, S(VIu,VCc) - коэффициент схожести между вертикальным нечетким представлением VIu и VCc. Веса w1 и w2 - числа с плавающей точкой в интервале [0,1], так что w1 + w2 = 1. Коэффициенты схожести S(HIu,HCc) и S(VIu,VCc) являются суммой коэффициентов схожести между парами соответствующих нечетких полос в горизонтальном и вертикальном представлениях:
S(HIu,HCc) = ![]() S(Xu,k,
S(Xu,k, ![]() ) (13)
) (13)
S(VIu,VCc) = ![]() S(Yu,t,
S(Yu,t, ![]() ) (14)
) (14)
где веса weightHc,k и weightVc,t €[0,1]. ![]() =1.
=1. ![]() =1. S(Xu,k,
=1. S(Xu,k, ![]() ) – коэффициент схожести горизонтальных нечетких полос Xu,k,
) – коэффициент схожести горизонтальных нечетких полос Xu,k, ![]() , S(Yu,t,
, S(Yu,t, ![]() ) - коэффициент схожести вертикальных нечетких полос Yu,t,
) - коэффициент схожести вертикальных нечетких полос Yu,t, ![]() .
.
Коэффициент схожести двух нечетких полос вычисляется с помощью взвешенного расстояния Евклида:
S(Xu,k, ![]() ) =
) = ![]() (15)
(15)
S(Yu,t, ![]() ) =
) = ![]() (16)
(16)
На каждом шаге вычисления коэффициента схожести Sc(Iu,Cc) необходимо использовать определенные веса. Выбор значений для весов зависит от приложения, благодаря тому факту, что различные регионы пространства объекта могут иметь различные степени важности, которые характеризируют этот объект. Обычно рассматривается случай, когда распределение горизонтального и вертикального представлений для коэффициента схожести имеют одинаковую важность.
Следовательно, w1 = w2 = 1/2. А. В (12) веса weightHc,k выбираются таким образом, чтобы придать большую степень важности горизонтальной нечеткой полосе Xc,k. Они являются мерой релевантности горизонтальной нечеткой полосы Xc,k по отношению к другим горизонтальным нечетким полосам. Подобные рассуждения могут быть использованы для вертикальных нечетких полос. В эксперименте используется следующее выражение:
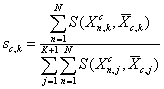 (17)
(17)
где ![]() - коэффициент схожести между к-тым горизонтальным нечетким представлением
- коэффициент схожести между к-тым горизонтальным нечетким представлением ![]() , n-того экземпляра класса с и Xc,к. Коэффициент схожести
, n-того экземпляра класса с и Xc,к. Коэффициент схожести ![]() вычисляется, используя выражение (15), в котором веса qt выбираются с учетом предыдущих коэффициентов схожести, чтобы придать большую степень важности прямоугольнику Rt,k, а именно:
вычисляется, используя выражение (15), в котором веса qt выбираются с учетом предыдущих коэффициентов схожести, чтобы придать большую степень важности прямоугольнику Rt,k, а именно:
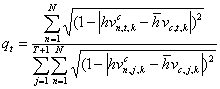 (18)
(18)
Классификация неизвестного объекта выполняется путем определения того класса с, который дает наибольший коэффициент схожести.
Выводы
В данной работе рассматривается процесс распознавания образов (на примере идентификации человека) с использованием математического аппарата нечеткой логики. Для построения системы распознавания объектов необходимо обеспечить как минимум три основных этапа, а именно: улучшение качества изображения путем фильтрации шумовых составляющих, сегментации или кластеризации объектов, присутствующих на изображении, и, наконец, классификации образов. Следует отметить, что результат распознавания в одинаковой степени зависит от качества каждого из этапов, причем если на предыдущем этапе был получен негативный результат, то последующие этапы только усилят эту ошибку, что в целом даст негативный результат для системы распознавания в целом.
Еще одним важным моментом, который необходимо отметить, является то, что на этапе классификации образов огромную роль играет набор входных данных для процесса классификации. Если этот набор избыточный или, наоборот, недостаточный, то это также отразиться на качестве распознавания. Как правило, непосредственно перед процессом классификации выполняется процедура выделения характерных признаков во входной информации, т.е. выделение наиболее значимой информации и игнорирование малозначащей. Для выделения наиболее значимой информации можно использовать метод, описанный в [10]. Таким образом, можно сделать вывод, что теория нечетких множеств становится мощным инструментов для построения интеллектуальных аппаратно-программных систем распознавания образов.
In work application of the theory of fuzzy sets for realization of process of recognition of graphic images for human identification is considered. The basic attention is given to algorithmic features of realization of functions of recognition with use of fuzzy operations.
1. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH – СПб.:БХВ-Петербург, 2003. – 736 с.: ил.
2. Lotfi A. Zadeh. Foreword – Recognition Technology and Fuzzy Logic // IEEE TRANSACTION ON FUZZY SYSTEM, VOL.9, NO.1, FEBRUARY 2001.
3. Detlef Nauck and Rudolf Kruse. New learning strategies for NEFCLASS. In Proc. Seventh International Fuzzy Systems Association World Congress IFSA'97, Vol. IV, pp. 50-55, Academia Prague, 1997.
4. Detlef Nauck and Rudolf Kruse. What are neuro-fuzzy classifiers? In Proc. Seventh International Fuzzy Systems Association World Congress IFSA'97, Vol. IV, pp. 228-233, Academia Prague, 1997.
5. Detlef Nauck. Building neural fuzzy controllers with NEFCON-I. In Rudolf Kruse, Jorg Gebhardt, and Rainer Palm, editors, Fuzzy Systems in Computer Science, Artificial Intelligence, pages 141-151. Vieweg, Wiesbaden, 1994.
6. V. Boskovitz, H. Guterman. An Adaptive Neuro-Fuzzy System for Automatic Image Segmentation and Edge Detection // IEEE TRANSACTION ON FUZZY SYSTEM, VOL.10, NO.2, APRIL 2002.
7. L.O. Hall, A. Bensaid, L. Clark, R. Velthuizen, M.Silbiger, and J. Bezdek. A comparison of neural network an fuzzy clustering techniques in segmenting magnetic resonance images of the brain // IEEE TRANSACTION ON NEURAL NETWORK, VOL.3, SEPTEMBER 1992.
8. B. Lazerini, F. Marcelloni. A Fuzzy Approach to 2-D Shape Recognition // IEEE TRANSACTION ON FUZZY SYSTEM, VOL.9, NO.1, FEBRUARY 2001.
9. Я.Ю.Дорогой. Реализация офтольмогеометрического подхода к идентификации человека. //Вісник НТУУ «КПІ», «Інформатика, управління та обчислювальна техніка», №44. – 2006. – С. 240-253.
10. Я.Ю.Дорогой. Оценка значимости признаков на основе многослойных нейронных сетей в системах диагностики автотранспорта //Автомобильный транспорт, №13, 2003. – с. 52-55.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Информационно-измерительные системы
Ковальов О.І. Вимірювання у процесно-орієнтованих стандартахПолякова М.В., Ищенко А.В., Худайбердин Э.И. Порогово-пространственная сегментация цветных текстурированных изображений на основе метода JSEG
Дзюбаненко А. В. Организация компьютерных систем для анализа изображений
Гордеев Б.Н., Зивенко А.В., Наконечный А.Г. Формирование зондирующих импульсов для полиметрических измерительных систем
Богданов А.В., Бень А.П., Хойна С.И. Релаксация обратного тока диодов Шоттки после их магнитно-импульсной обработки (МИО)
Тверезовский В.С., Бараненко Р.В. Проектирование измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Оптимизированная модель измерителя доб-ротности варикапов
Руднєва М.С., Кочеткова О.В., Задорожній Р.О. Принципи побудови оптимальної структури інформаційно-вимірювальної системи геометричних розмірів об’єктів в діапазоні від 1 нм до 1000 нм
Биленко М.С., Рожков С.А., Единович М.Б. Идентификация деформаций пе-риодических структур с использованием систем технического зрения
Рашкевич Ю.М., Ковальчук А.М., Пелешко Д.Д. Афінні перетворення в модифікаціях алгоритму RSA шифрування зображень
Дидык А.А., Фефелов А.А, Литвиненко В.И., Шкурдода С.В., Синяков Ф. В. Классификация масс-спектров с помощью кооперативного иммунного алгоритма
Клименко А.K. Обратная модель для решения задач в системах с многосвязными динамическими объектами
Завгородній А.Б. Порівняльне дослідження твердотільних і рідиннофазних об'єктів методом газорозрядної візуалізації
Голощапов С.С., Петровский А.В., Рожко Ж.А., Боярчук А.И. Измерение доб-ротности колебательного контура на основе метода биения частот
Кириллов О.Л., Якимчук Г.С. Диагностирование критерия безопасности при заполнении замкнутых объемов СПЖ косвенным методом
Долина В.Г. Проблеми підвищення точності рефрактометра на основі прозорих порожнистих циліндрів.
Самков О.В., Захарченко Ю.А. Застосування алгоритму клонального відбору для побудови планів модернізації авіаційної техніки
Попов Д.В. Метод формування регламентів технічного обслуговування повітряних суден
Казак В.М., Чорний Г.П., Чорний Т.Г. Оцінювання готовності технічних об’єктів з урахуванням достовірності їх контролю
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования цифрового измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования устройства для разбраковки варикапов по емкостным параметрaм и добротности
Сосюк А.В. Інтелектуальний автоматизований контроль знань в системах дистанційного навчання
Соколов А.Є. Деякі аспекти систезу комп’ютеризованої адаптивної системи навчання
Полякова М.В., Волкова Н.П., Іванова О.В. Сегментація зображень стохастичних текстур амплітудно-детекторним методом у просторі вейвлет-перетворення
Луцкий М.Г., Пономаренко А.В., Филоненко С.Ф. Обработка сигналов акустической эмиссии при определении положения сквозных дефектов
Литвиненко В.И., Дидык А.А., Захарченко Ю.А. Компьютерная система для решения задач классификации на основе модифицированных иммунных алгоритмов
Лубяный В.З., Голощапов С.С. Прямоотсчетные измерители расхождений емкостей
Беляев А.В. Построение навигации для иерархических структур в WEB-системах и системах управления WEB-сайтом
Терновая Т.И., Сумская О.П., Слободянюк И.И., Булка Т.И. Контроль качества тканей специального назначения с помощью автоматических систем.
Шеховцов А.В. Інформаційний аспект: розпізнавання образів індивідуума.
Полякова М.В. Определение границ сегмента упорядоченной текстуры на изображении с однородным фоном с помощью многоканального обнаружения пачки импульсов.
Литвиненко В.И. Прогнозирования нестационарных временных рядов с помощью синтезируемых нечетких нейронных сетей
Ковриго Ю.М., Мисак В.Ф., Мовчан А.П., Любицький С.В. Автоматизована система діагностики генераторів електростанцій
Браїловський В.В., Іванчук М.М., Ватаманюк П.П., Танасюк В.С. Керований детектор імпульсного ЯКР спектрометра
Забытовская О.И. Построение функции полезности по экспериментальным данным.
Шиманські З. Апаратні засоби сегментації мовного сигналу
Хобин В.А., Титлова О.А. К вопросу измерения парожидкостного фронта в дефлегматоре абсорбционно-диффузионной холодильной машины (АДХМ)
Фефелов А. А. Использование байесовских сетей для решения задачи поиска места и типа отказа сложной технической системы
Слань Ю. М., Трегуб В. Г. Оперативна нейромережна ідентифікація складних об’єктів керування
Ролик А.И. Модель управления перераспределением ресурсов информационно-телекоммуникационной системы при изменении значимости бизнес-процессов
Кириллов О.Л., Якимчук Г.С., Якимчук С.Г. Изучение электрического поля с помощью датчика измерителя электростатического потенциала на модели замкнутого металлического объема
Грицик В.В. Застосування штучних нейронних мереж при проектуванні комп’ютерного зору.
Гасанов А.С. Информационные технологии построения систем прогнозирования отказов
Шеховцов А.В., Везумский А.К., Середа Е.С. Алгоритм сжатия информации без потерь: модифицированный алгоритм LZ77
Ходаков В.Е., Жарикова М.В., Ляшенко Е.Н. Методы и алгоритмы визуализации пространственных данных на примере моделирования распространения лесных пожаров.
Полякова М.В., Крылов В.Н. Обобщённые масштабные функции с компактным носителем в задаче сегментации изображений упорядоченных текстур. – C. 75 – 84.
Литвиненко В.И. Синтез радиально-базисных сетей для решения задачи дистанционного определения концентрации хлорофилла.
Бражник Д.А. Управление совмещением изображения объекта в сцене и эталонного изображения.
Бабак В.П., Пономаренко А.В. Локализация места положения сквозных дефектов по сигналам акустической эмиссии.
Мороз В. В. R-D проблема и эффективность систем сжатия изображений.
Крылов В.Н., Полякова М.В., Волкова Н.П. Контурная сегментация в пространстве гиперболического вейвлет-преобразования с использованием математической морфологии.
Квасников В.П., Баранов А.Г. Анализ влияния дестабилизирующих факторов на работу биканальной координатно-измерительной машины.
Казак В.М., Гальченко С.М., Завгородній С.О. Аналіз можливості застосування імовірнісних методів розпізнавання для виявлення пошкоджень зовнішнього обводу літака.
Тищенко И.А., Лубяный В.З. Управление коммутационными процессами в интегрированных сетях связи.
Корниенко-Мифтахова И.К.,Филоненко С.Ф. Информационно-измерительная система для анализа характеристик динамического поведения конструкций.
Тверезовский В.С., Бараненко Р.В. Модель измерителя емкости с линейной шкалой измерений.
Полякова М.В., Крылов В.Н. Мультифрактальный метод автоматизированного распознавания помех на изображении.
Рожков С.О., Федотова О.М. Алгоритм розпізнавання дефектів тканин для автоматичної системи контролю якості.
Бражник Д.А. Использование проективного преобразования для автоматизации обнаружения объектов.
Ходаков В.Є., Шеховцов А.В., Бараненко Р.В. Математичні аспекти створення автоматизованої системи „Реєстр виборців України”