УДК 681.3.01:519.67
ОБОБЩЁННЫЕ МАСШТАБНЫЕ ФУНКЦИИ С КОМПАКТНЫМ НОСИТЕЛЕМ В ЗАДАЧЕ СЕГМЕНТАЦИИ ИЗОБРАЖЕНИЙ УПОРЯДОЧЕННЫХ ТЕКСТУР
Полякова М.В., Крылов В.Н.
Постановка проблемы. В данной работе рассматривается задача сегментации изображений упорядоченных текстур. Значительный интерес для решения практических задач представляют методы текстурной сегментации изображений с высокой помехоустойчивостью и низкой погрешностью определения координат точек границ текстурных областей. Этим требованиям удовлетворяют методы текстурной сегментации изображений, осуществляющие переход от значений признака сегментации к значениям интенсивности. Они включают процедуры оценки признака сегментации или величины, функционально связанной с этим признаком; сигнально-семантического преобразования (ССП), подчеркивающего границы между однородными областями изображения; пороговой и морфологической обработки потенциальных границ однородных текстурных областей [1].
Основное влияние на помехоустойчивость и погрешность определения границ однородных текстурных областей этих методов оказывают процедуры оценки признака сегментации или величины, функционально связанной с этим признаком, и ССП. Чтобы обеспечить высокую помехоустойчивость метода текстурной сегментации, ССП должно выделять только границы однородных текстурных областей, причем тех, которые имеют смысловую интерпретацию. С другой стороны, для снижения погрешности определения координат точек границ однородных текстурных областей результат ССП должен стремиться к совокупности d-функций, сосредоточенных в точках границ однородных текстурных областей изображения.
Анализ последних публикаций. Нерешенные части общей проблемы. В работах, посвященных методам текстурной сегментации изображений, чаще всего для перехода от значений признака сегментации к значениям интенсивности используются вейвлеты Габора [1]. Они представляют собой гауссианы, модулированные комплексными синусоидами и обладают следующими преимуществами:
¾ это единственные функции, которые достигают наименьшего значения длительности на ширину полосы, определяемого принципом неопределенности; это означает высокую избирательность вейвлетов Габора по частоте при сохранении пространственной локализации;
¾ существует предположение о том, что в зрительной коре человеческого мозга осуществляется разложение стимульного изображения по базису вейвлетов Габора;
¾ вейвлеты Габора реализуются как полосовые фильтры и могут быть настроены на частотное содержание изображения.
Однако применение вейвлетов Габора в задаче текстурной сегментации изображений не лишено недостатков, а именно, сохраняется проблема высокой погрешности определения координат точек границ однородных текстурных областей изображения, особенно для неравномерных текстур. Причиной этого является то, что результат ССП с вейвлетами Габора не позволяет получить совокупность d-функций, сосредоточенных в точках границ однородных текстурных областей изображения, т. к. вейвлеты Габора представляют собой регулярные функции. Эта проблема обусловлена также недостаточной пространственной локализацией вейвлетов Габора. Известно, что улучшению пространственной локализации анализирующих вейвлетов при сохранении их локализации по частоте способствует использование разных вейвлет-функций на разных масштабах вейвлет-преобразования — нестационарное вейвлет-преобразование [2]. Снижению погрешности определения координат точек границ однородных текстурных областей изображения способствует применение обобщенных функций [3]. Обобщенная функция — это математическое понятие, обобщающее классическое понятие функции. В понятии обобщенной функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять ее средние значения с помощью последовательности локально интегрируемых функций в малых окрестностях данной точки.
При использовании в составе ССП обобщенных функций последние целесообразно применять либо после умножения на некоторую бесконечно дифференцируемую функцию (регуляризации), либо представления обобщенной функции как предела последовательности регулярных функций. Применение регулярных функций, стремящихся в пределе к обобщенной функции, в качестве анализирующих на разных масштабах нестационарного вейвлет-преобразования позволяет реализовать ССП, которое в этом случае объединяет в себе функции оценки признака сегментации или величины, функционально связанной с этим признаком, а также подчеркивания границ между однородными областями изображения. В объединении этих двух процедур сегментации и заключается преимущество использования регулярных функций, стремящихся в пределе к обобщенной функции, в качестве анализирующих функций на разных масштабах нестационарного вейвлет-преобразования. При этом большие значения масштаба приводят к помехоустойчивой сегментации с высокой погрешностью определения координат точек границ между однородными областями изображения, а при малых значениях масштаба вейвлет-преобразования помехоустойчивость снижается, но снижается и погрешность определения координат границ текстурных областей. Однако обобщенные функции позволяют обеспечить лучшую пространственную локализацию по сравнению с вейвлетами Габора.
Целесообразно, чтобы обобщенные функции, применяющиеся в задаче текстурной сегментации изображений, обладали следующими свойствами:
¾ так как частотные свойства изображений локально изменяются в пространстве, обобщенные функции должны иметь различную пространственно-частотную локализацию;
¾ для того, чтобы обеспечить локализацию границ однородных текстурных областей изображения, обобщенные функции должны обладать компактным носителем;
¾ текстурное изображение содержит различные типы сигнатур (перепады или всплески значений интенсивности) на границах однородных текстурных областей, что обусловлено типом текстуры; поэтому при их анализе должны использоваться обобщенные функции как с нулевым средним (вейвлет-функции), так и с отличным от нуля средним (масштабные функции).
Далее в этой работе рассматриваются только обобщенные масштабные функции. Целью работы является снижение погрешности определения координат точек границ однородных областей при текстурной сегментации изображений упорядоченных текстур путём использования обобщенных масштабных функций с компактным носителем. При достижении поставленной цели решены следующие задачи:
¾ усовершенствована модель представления упорядоченной текстуры изображения путем учёта помеховой ситуации для построения методов текстурной сегментации с высоким качеством границ однородных текстурных областей;
¾ разработаны обобщенные масштабные функции с компактным носителем;
¾ разработана модель обработки изображений на основе ССП с последовательностью локально интегрируемых функций, которые приближают обобщенную масштабную функцию.
Математическая модель изображения упорядоченной текстуры. Первым этапом создания методов текстурной сегментации изображений, удовлетворяющих требованиям помехоустойчивости и низкой погрешности определения координат точек границ однородных текстурных областей, является моделирование изображения. Известно, что метод текстурной сегментации в пространстве преобразования с вейвлетами Габора [1] предполагает представление текстуры с помощью непроизводных элементов. Эта модель представления текстуры является структурной и не учитывает статистическую модель помеховой ситуации, возникающей при формировании изображений. Поэтому сформулируем структурно-статистическую модель текстурного изображения.
Пусть полутоновое текстурное изображение I(x, y), х=1, ..., N; y=1, …, М; представлено значениями интенсивности в точках (x, y), где x, y — пространственные координаты.
Для определения математической модели текстурного изображения предположим, что совокупность значений интенсивности і-й строки изображения I(x, yi) включает n равномерных текстур ![]() . Текстуры
. Текстуры ![]() характеризуются соответственно разными непроизводными элементами
характеризуются соответственно разными непроизводными элементами ![]() , представляющими собой детерминированные функции пространственной координаты х, для которых существует преобразование Фурье. Равномерная текстура
, представляющими собой детерминированные функции пространственной координаты х, для которых существует преобразование Фурье. Равномерная текстура ![]() , состоящая из равноотстоящих непроизводных элементов
, состоящая из равноотстоящих непроизводных элементов ![]() определяется формулой
определяется формулой
![]() ,
,
где ![]() — период следования непроизводных элементов,
— период следования непроизводных элементов, ![]() — их количество в k-й текстурно однородной области і-й строки изображения, “*”— оператор свертки. Так как совокупность значений интенсивности і-й строки изображения I(x,yi) представлена текстурами
— их количество в k-й текстурно однородной области і-й строки изображения, “*”— оператор свертки. Так как совокупность значений интенсивности і-й строки изображения I(x,yi) представлена текстурами ![]() , разобьем область определения [0, N] строки изображения на n сегментов точками
, разобьем область определения [0, N] строки изображения на n сегментов точками ![]() так, чтобы каждый сегмент [
так, чтобы каждый сегмент [![]() ] или интервал
] или интервал ![]() , представлял однородную текстурную область изображения.
, представлял однородную текстурную область изображения.
Однородная текстурная область изображения в терминах значений интенсивности его і-й строки определяется фрагментом текстуры ![]() :
:
![]() ,
,
где 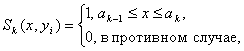 если однородная текстурная область замкнута и
если однородная текстурная область замкнута и 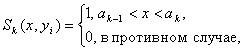 если область открытая.
если область открытая.
Однородные текстурные области составляют текстурное изображение, тогда
![]() , (1)
, (1)
где ![]() — i-я строка незашумленного изображения.
— i-я строка незашумленного изображения.
При формировании изображений существенно влияние внутренних шумов датчиков различной физической природы. Адекватной моделью собственных шумов датчиков согласно [4] является адитивная гауссовская модель:
![]() , (2)
, (2)
где ![]() — i-я строка зашумленного изображения,
— i-я строка зашумленного изображения, ![]() — i-я строка незашумленного изображения,
— i-я строка незашумленного изображения, ![]() — независимые нормально распределенные наблюдения с нулевым средним и дисперсией
— независимые нормально распределенные наблюдения с нулевым средним и дисперсией ![]() .
.
Структурно-статистическая модель i-й строки текстурного изображения с учетом (1), (2) принимает вид:
![]() .
.
Обобщенные масштабные функции с компактным носителем. Для текстурной сегментации изображений с низкой погрешностью определения координат точек границ однородных текстурных областей построим на основе двумасштабного разностного уравнения обобщенные масштабные функции с компактным носителем. Двумасштабное разностное уравнение использовалось для математического описания информационного содержания изображения при его представлении на двух масштабах. Как показано в работах [5, 6], к решению двумасштабного разностного уравнения сводится задача построения базисов вейвлетов с компактным носителем.
Двумасштабное разностное уравнение — это функциональное уравнение вида
![]() , (3)
, (3)
где ![]()
![]() — константы. В зависимости от значений коэффициентов уравнения (3) его решения могут представлять собой интегрируемые функции или обобщенные функции. Решения (3), представляющие интегрируемые функции, широко известны в вейвлет-анализе как масштабные функции (scaling functions).
— константы. В зависимости от значений коэффициентов уравнения (3) его решения могут представлять собой интегрируемые функции или обобщенные функции. Решения (3), представляющие интегрируемые функции, широко известны в вейвлет-анализе как масштабные функции (scaling functions).
Пример интегрируемого решения уравнения (3) с коэффициентами ![]()
![]()
![]() — вейвлет Добеши 2-го порядка — показан на рис. 1, а. Пример решения уравнения (3) с коэффициентами
— вейвлет Добеши 2-го порядка — показан на рис. 1, а. Пример решения уравнения (3) с коэффициентами ![]()
![]() ,
, ![]() ,
, 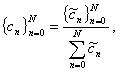 в пространстве обобщенных функций показан на рис. 1, б.
в пространстве обобщенных функций показан на рис. 1, б.
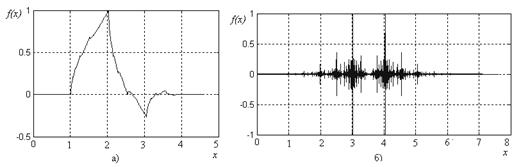
Рис. 1 Интегрируемое решение (3) (а) и решение (3) в пространстве обобщенных функций (б).
В задачах сжатия, обработки и распознавания изображений в настоящее время используются только интегрируемые решения уравнения (3). Они применяются при построении вейвлетов как функции, локализованные как в исходном пространстве, так и в области преобразования Фурье, что связано с необходимостью применения к нестационарным сигналам локального пространственно-частотного анализа. Обобщенные функции позволяют обеспечить лучшую пространственную локализацию по сравнению с интегрируемыми функциями. В соответствии с целью сегментации мы предлагаем использовать некоторые решения уравнения (3) в пространстве обобщенных функций при решении задачи текстурной сегментации изображений. А именно, для снижения погрешности определения координат точек границ однородных текстурных областей изображения целесообразно применять ССП на основе последовательности локально интегрируемых функций, стремящихся в пределе к обобщенной функции.
Приведем утверждения, касающиеся существования и свойств решений (3). Уравнение (3) предполагает существование двух масштабов, на которых анализируется f(х), а также, что значения f(х) на большем масштабе представляют собой результат преобразования подобия и сдвига этой же функции на меньшем масштабе. В частном случае (3) , когда a и bn — целые, это уравнение принимает вид
![]() . (4)
. (4)
Уравнение (3) всегда имеет решение в смысле обобщенных функций. Определим, при каких условиях на коэффициенты уравнения (3) его решения в пространстве обобщенных функций целесообразно использовать для сегментации изображений упорядоченных текстур. Приведем сначала утверждения, касающиеся решений (3), принадлежащих пространству ![]() функций, модуль которых интегрируем на пространстве вещественных чисел.
функций, модуль которых интегрируем на пространстве вещественных чисел.
Выполнив преобразование Фурье (3), имеем
![]() ,
,
где ![]() — частота, а
— частота, а
![]() . (5)
. (5)
Обозначим
![]() . (6)
. (6)
Совокупность решений (3), принадлежащих пространству ![]() , определяется следующей теоремой [5].
, определяется следующей теоремой [5].
Теорема 1.
Если ![]() и
и ![]() , существует только тривиальное решение (3) из пространства
, существует только тривиальное решение (3) из пространства ![]() .
.
Если ![]() , существует не более одного нетривиального решения (3) из пространства
, существует не более одного нетривиального решения (3) из пространства ![]() . Если такое решение существует, то его преобразование Фурье определяется формулой
. Если такое решение существует, то его преобразование Фурье определяется формулой
![]() , (7)
, (7)
где константа ![]() и бесконечное произведение в (7) сходится для любого w.
и бесконечное произведение в (7) сходится для любого w.
Если ![]() , то преобразование Фурье любого решения (3) из пространства
, то преобразование Фурье любого решения (3) из пространства ![]() имеет вид:
имеет вид:
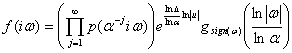 , (8)
, (8)
где ![]() ,
,
![]() — непрерывные периодические функции с периодом 1;
— непрерывные периодические функции с периодом 1;
![]() , где
, где ![]() ,
, ![]() ; причем бесконечное произведение в (8) сходится для любого w. Обратно, если
; причем бесконечное произведение в (8) сходится для любого w. Обратно, если ![]() — непрерывные периодические функции с периодом 1 такие, что обратное преобразование Фурье правой части (8) принадлежит пространству
— непрерывные периодические функции с периодом 1 такие, что обратное преобразование Фурье правой части (8) принадлежит пространству ![]() , то f(х) удовлетворяет уравнению (3).
, то f(х) удовлетворяет уравнению (3).
Теорема 1 определяет явный вид решения уравнения (3) в частотной области, т. к. в пространственной области решение (3) в явном виде удается получить только в исключительных случаях.
При моделировании текстур высокочастотные компоненты изображения обычно не учитывают, поэтому рассмотрим решения уравнения (3), преобразование Фурье которых определяется формулой (7) для Δ=1. Имеет место следующее следствие теоремы 1.
Следствие. Пусть двумасштабное разностное уравнение (3) с Δ=1 имеет нетривиальное решение f(x)ÎL1(R). Тогда![]() и f(x) имеет компактный носитель
и f(x) имеет компактный носитель ![]() .
.
Доказательство этого следствия [5] показывает, что двумасштабное разностное уравнение (3) с Δ=1 всегда обладает единственным с точностью до масштабного множителя решением f(х) в пространстве обобщенных функций ![]() . Это решение f(х) имеет компактный носитель
. Это решение f(х) имеет компактный носитель ![]() , а его преобразование Фурье определяется формулой (7).
, а его преобразование Фурье определяется формулой (7).
В дальнейшем в этой работе оценим целесообразность применения в задаче текстурной сегментации изображений решений частного случая уравнения (3) — уравнения (4) с Δ=1, которые принадлежат пространству обобщенных функций и имеют компактный носитель.
При решении задач анализа и сегментации изображений возникает необходимость обработки дискретных данных, поэтому явный вид решения (3) необходим для построения фильтров, согласованных с моделью текстуры. Решения уравнения (3) в пространственной области в явном виде получены только для некоторых значений его коэффициентов. Поэтому рассмотрим процесс приближенного вычисления решений уравнения (3) в пространственной области.
Каскадный алгоритм. Заметим, что двумасштабное разностное уравнение может быть представлено как однородное интегральное уравнение Фредгольма второго рода [7]. Интегральным уравнением называется уравнение, которое содержит неизвестную функцию под знаком интеграла. Например, интегральным уравнением относительно ![]() является уравнение
является уравнение
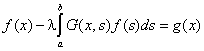 ,
,
где ![]() ,
, ![]() — принимающие вещественные или комплексные значения известные функции переменных
— принимающие вещественные или комплексные значения известные функции переменных ![]() — параметр. Уравнение (9) называется уравнением Фредгольма второго рода. Для этого уравнения предполагают, что ядро
— параметр. Уравнение (9) называется уравнением Фредгольма второго рода. Для этого уравнения предполагают, что ядро ![]() и свободный член
и свободный член ![]() являются квадратично интегрируемыми функциями. В случае
являются квадратично интегрируемыми функциями. В случае ![]() уравнение (9) называется однородным.
уравнение (9) называется однородным.
Очевидно, что двумасштабное разностное уравнение (3) представляет собой однородное уравнение Фредгольма второго рода, причем переменная ![]() под знаком интеграла принимает конечное число дискретных значений и интеграл заменен суммой. Решение уравнения (9) и, следовательно, двумасштабного разностного уравнения (3) может быть получено итерационно с помощью метода последовательных приближений. Он заключается в следующем [7].
под знаком интеграла принимает конечное число дискретных значений и интеграл заменен суммой. Решение уравнения (9) и, следовательно, двумасштабного разностного уравнения (3) может быть получено итерационно с помощью метода последовательных приближений. Он заключается в следующем [7].
Пусть свободный член и ядро уравнения Фредгольма являются непрерывными функциями (первая — на ![]() , вторая — на
, вторая — на ![]() ). Выберем какую-нибудь непрерывную функцию
). Выберем какую-нибудь непрерывную функцию ![]() и подставим ее в правую часть уравнения (9). Получим
и подставим ее в правую часть уравнения (9). Получим
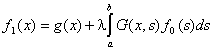 ,
,
причем ![]() также непрерывна на
также непрерывна на ![]() . Продолжая этот процесс, получим последовательность функций
. Продолжая этот процесс, получим последовательность функций ![]() ,
, ![]() , …,
, …, ![]() , …, удовлетворяющих уравнениям
, …, удовлетворяющих уравнениям
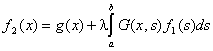 , …,
, …, 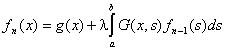 , …
, …
Из этих уравнений следует, что
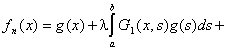
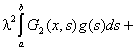
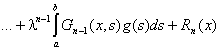 ,
,
где 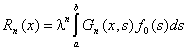 , а
, а ![]() — итерированные ядра, определяемые рекуррентной формулой
— итерированные ядра, определяемые рекуррентной формулой
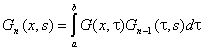 ,
, ![]()
![]() .
.
Известно [7], что при ![]() выполняется
выполняется ![]() и
и ![]() , где
, где ![]() — решение уравнения Фредгольма второго рода.
— решение уравнения Фредгольма второго рода.
С помощью метода последовательных приближений может быть получено как решение двумасштабного разностного уравнения (3), так и его частного случая — уравнения (4).
Итеративный метод поиска решения двумасштабного разностного уравнения на решетке (4) известен как каскадный алгоритм [6]. Согласно этому алгоритму решение (4) представляет собой фиксированную точку f(х)=Gf(х) линейного оператора
![]() ,
,
получаемую в результате применения итеративной схемы fj(х)=Gfj-1(х) к начальному приближению вида
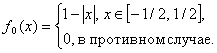
Построение ![]() , если известно
, если известно ![]() , включает три этапа:
, включает три этапа:
1) выделяют сегменты длиной ![]() , на которых
, на которых ![]() постоянна;
постоянна;
2) заменяют значения ![]() на каждом из этих сегментов промасштабированной и сдвинутой версией
на каждом из этих сегментов промасштабированной и сдвинутой версией ![]() ;
;
3) суммируют полученные компоненты ![]() .
.
Последнее означает, что значения ![]() могут быть вычислены путем использования только значений
могут быть вычислены путем использования только значений ![]() в малой окрестности
в малой окрестности ![]() . Например, в случае j=1,
. Например, в случае j=1, 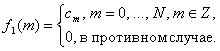
Т. к. любое приближение ![]() является суммой промасштабированных и сдвинутых версий
является суммой промасштабированных и сдвинутых версий ![]() , процесс его построения представляют графически с помощью гистограммы. Тогда начальное приближение каскадного алгоритма
, процесс его построения представляют графически с помощью гистограммы. Тогда начальное приближение каскадного алгоритма
![]()
представляет собой одиночный импульс длительности 1. ![]() изображают прямоугольными импульсами длительности 0,5,
изображают прямоугольными импульсами длительности 0,5, ![]() — импульсами длительности
— импульсами длительности ![]() с амплитудой
с амплитудой ![]()
![]() . Множитель
. Множитель ![]() вводится для нормализации.
вводится для нормализации.
Если существует непрерывное решение (3), а также если решение (3) существует лишь в пространстве обобщенных функций, каскадный алгоритм сходится к этому решению в смысле обобщенных функций, т. е. ![]() сходятся к обобщенной функции
сходятся к обобщенной функции ![]() (рис. 2).
(рис. 2).
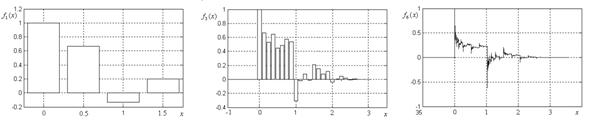
Рис. 2 [6]. Построение последовательности функций ![]() , имеющей предел в пространстве обобщенных функций, представленное с помощью гистограмм:
, имеющей предел в пространстве обобщенных функций, представленное с помощью гистограмм: ![]() (а),
(а), ![]() (б),
(б), ![]() (в)
(в) ![]() .
.
Заметим, что в процессе последовательных приближений каждая функция ![]() зависит от выбора начальной функции
зависит от выбора начальной функции ![]() . Однако предельная функция от выбора
. Однако предельная функция от выбора ![]() не зависит. Cогласно теореме 1, решения двумасштабного разностного уравнения (3) имеют отличное от нуля среднее и определяют масштабные функции вейвлет-анализа.
не зависит. Cогласно теореме 1, решения двумасштабного разностного уравнения (3) имеют отличное от нуля среднее и определяют масштабные функции вейвлет-анализа.
Реализация ССП изображения в пространстве обобщенных функций с компактным носителем. Известно, что хорошей локализацией в пространстве обладают сингулярные обобщенные функции. Дискретизируем функции ![]() , j=1, 2, …, полученные в результате применения каскадного алгоритма для вычисления обобщенной масштабной функции
, j=1, 2, …, полученные в результате применения каскадного алгоритма для вычисления обобщенной масштабной функции ![]() с компактным носителем. Получаем дискретные последовательности
с компактным носителем. Получаем дискретные последовательности ![]() , j=1, 2, …, где Nj — количество коэффициентов соответствующих последовательностей. Эти дискретные последовательности используем в качестве банка фильтров при выполнении ССП для текстурной сегментации изображений.
, j=1, 2, …, где Nj — количество коэффициентов соответствующих последовательностей. Эти дискретные последовательности используем в качестве банка фильтров при выполнении ССП для текстурной сегментации изображений.
Пример импульсных характеристик фильтров, полученных в результате дискретизации ![]() и представляющих собой приближенные решения уравнения
и представляющих собой приближенные решения уравнения
![]() (10)
(10)
в пространстве обобщенных функций с компактным носителем, показан на рис. 3. В качестве коэффициентов уравнения (10) ![]() выбрана последовательность
выбрана последовательность ![]() , нормированная к единице.
, нормированная к единице.
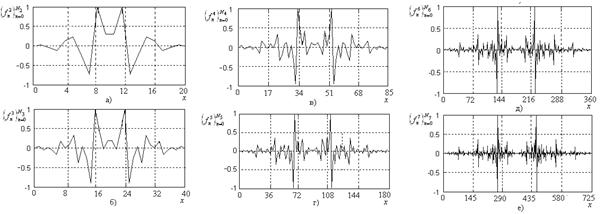
Рис. 3 Импульсные характеристики фильтров ![]() для j=2 (а), 3 (б), 4 (в), 5 (г), 6 (д), 7 (е).
для j=2 (а), 3 (б), 4 (в), 5 (г), 6 (д), 7 (е).
Основные положения этой работы проверялись на тестовом изображении, размером 512х512 пикселей, представляющем собой однородную область упорядоченной текстуры на фоне (рис. 4, а).
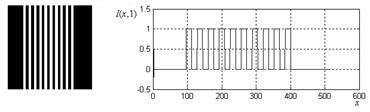
а) б)
Рис. 4 Тестовое изображение (а) и его строка (б).
Это изображение незашумлено и описывается моделью (1). Непроизводный элемент текстуры согласно модели (1), ![]() представляет собой одиночный импульс, протяженностью 16 пикселей. Фрагмент текстуры
представляет собой одиночный импульс, протяженностью 16 пикселей. Фрагмент текстуры ![]() состоит из последовательности десяти импульсов, равноотстоящих друг от друга на расстоянии Dх=16 пикселей. Обработка тестового изображения производилась с помощью фильтров, полученных в результате дискретизации функций
состоит из последовательности десяти импульсов, равноотстоящих друг от друга на расстоянии Dх=16 пикселей. Обработка тестового изображения производилась с помощью фильтров, полученных в результате дискретизации функций ![]() , j=2, 3, 4, 5, 6, 7. Для построения
, j=2, 3, 4, 5, 6, 7. Для построения ![]() коэффициенты уравнения (10) сn, n=0, …, N выбирались как
коэффициенты уравнения (10) сn, n=0, …, N выбирались как ![]() =
= ![]() , N=7. Последовательности
, N=7. Последовательности ![]() , j=2, …, 7, нормировались к единице.
, j=2, …, 7, нормировались к единице.
На рис. 4, б представлена строка тестового изображения, а на рис. 5, а – результат ее обработки с помощью фильтра ![]() , реализующего
, реализующего ![]() .
.
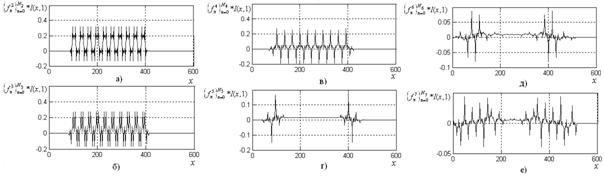
Рис.5 Строка изображения с рис. 3, б в пространстве преобразования с фильтрами ![]() , j=2 (a), 3 (б), 4 (в), 5 (г), 6 (д), 7 (е).
, j=2 (a), 3 (б), 4 (в), 5 (г), 6 (д), 7 (е).
Непроизводные элементы текстуры и однородная текстурная область имеют в пространстве коэффициентов преобразования равные максимумы в области перепадов интенсивности (рис. 5, а — в). При увеличении номера итерации каскадного алгоритма j относительные размеры пиков непроизводных элементов уменьшаются (рис. 5, г), в то же время увеличивается амплитуда пиков на границах текстурной области изображения. Т. о., с помощью функций, полученных в результате каскадного алгоритма и сходящихся к обобщенной масштабной функции, можно регулировать детальность описания текстуры изображения.
Выводы. В работе разработан математический аппарат сигнально-семантического преобразования изображений упорядоченных текстур, позволяющий получить подчеркнутые границы текстурно-однородных областей. Для реализации процедуры сегментации с использованием этого преобразования могут быть использованы как дифференциальные, так и корреляционно-экстремальные методы в соответствии с требованиями к помехоустойчивости и погрешности определения координат точек границ однородных текстурных областей.
Тempered distribution scaling functions with compact support is defined. The model of image processing based on signal-semantic transform with the sequence of local integrable functions which approximate the tempered distribution is proposed.
1. Dunn D., Higgins W.E., Wakeley J. Texture segmentation using 2D Gabor elementary function // IEEE Trans. on PAMI. — 1994. — Vol.16, № 2. — P. 130 — 149.
2. Cohen A., Sere E. Time-frequency localization with non-stationary wavelet packets. // Subband and Wavelet Transforms: Design and Application / Akansu A.N., Smith M.J.T. (eds.) — Kluwer, 1996. — P. 54 — 81.
3. Гельфанд И.М., Шилов Г.Е. Обобщенные функции и действия над ними. Вып. 1. — М.: Физматгиз, 1959. — 470 с.
4. Крылов В.Н., Максимов М.В. Вторичные преобразователи сигналов изображений. — Одесса: Астропринт, 1997. — 176 с.
5. Daubechies I., Lagarias J.C. Two-scale difference equations. I. Existence and global regularity of solutions // SIAM J. Math. Anal. — 1991. — Vol. 22, № 5. — P. 1388 — 1410.
6. Daubechies I. Orthonormal bases of compactly supported wavelets // Comm. Pure Appl. Math. — 1988. — Vol. 41. — P. 909 — 996.
7. Городецкий В.В., Нагнибида Н.И., Настасиев П.П. Методы решения задач по функциональному анализу: Учеб. пособие. — К.: Выща шк., 1990. — 479 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Информационно-измерительные системы
Ковальов О.І. Вимірювання у процесно-орієнтованих стандартахПолякова М.В., Ищенко А.В., Худайбердин Э.И. Порогово-пространственная сегментация цветных текстурированных изображений на основе метода JSEG
Дзюбаненко А. В. Организация компьютерных систем для анализа изображений
Гордеев Б.Н., Зивенко А.В., Наконечный А.Г. Формирование зондирующих импульсов для полиметрических измерительных систем
Богданов А.В., Бень А.П., Хойна С.И. Релаксация обратного тока диодов Шоттки после их магнитно-импульсной обработки (МИО)
Тверезовский В.С., Бараненко Р.В. Проектирование измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Оптимизированная модель измерителя доб-ротности варикапов
Руднєва М.С., Кочеткова О.В., Задорожній Р.О. Принципи побудови оптимальної структури інформаційно-вимірювальної системи геометричних розмірів об’єктів в діапазоні від 1 нм до 1000 нм
Биленко М.С., Рожков С.А., Единович М.Б. Идентификация деформаций пе-риодических структур с использованием систем технического зрения
Рашкевич Ю.М., Ковальчук А.М., Пелешко Д.Д. Афінні перетворення в модифікаціях алгоритму RSA шифрування зображень
Дидык А.А., Фефелов А.А, Литвиненко В.И., Шкурдода С.В., Синяков Ф. В. Классификация масс-спектров с помощью кооперативного иммунного алгоритма
Клименко А.K. Обратная модель для решения задач в системах с многосвязными динамическими объектами
Завгородній А.Б. Порівняльне дослідження твердотільних і рідиннофазних об'єктів методом газорозрядної візуалізації
Голощапов С.С., Петровский А.В., Рожко Ж.А., Боярчук А.И. Измерение доб-ротности колебательного контура на основе метода биения частот
Кириллов О.Л., Якимчук Г.С. Диагностирование критерия безопасности при заполнении замкнутых объемов СПЖ косвенным методом
Долина В.Г. Проблеми підвищення точності рефрактометра на основі прозорих порожнистих циліндрів.
Самков О.В., Захарченко Ю.А. Застосування алгоритму клонального відбору для побудови планів модернізації авіаційної техніки
Попов Д.В. Метод формування регламентів технічного обслуговування повітряних суден
Казак В.М., Чорний Г.П., Чорний Т.Г. Оцінювання готовності технічних об’єктів з урахуванням достовірності їх контролю
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования цифрового измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования устройства для разбраковки варикапов по емкостным параметрaм и добротности
Сосюк А.В. Інтелектуальний автоматизований контроль знань в системах дистанційного навчання
Соколов А.Є. Деякі аспекти систезу комп’ютеризованої адаптивної системи навчання
Полякова М.В., Волкова Н.П., Іванова О.В. Сегментація зображень стохастичних текстур амплітудно-детекторним методом у просторі вейвлет-перетворення
Луцкий М.Г., Пономаренко А.В., Филоненко С.Ф. Обработка сигналов акустической эмиссии при определении положения сквозных дефектов
Литвиненко В.И., Дидык А.А., Захарченко Ю.А. Компьютерная система для решения задач классификации на основе модифицированных иммунных алгоритмов
Лубяный В.З., Голощапов С.С. Прямоотсчетные измерители расхождений емкостей
Беляев А.В. Построение навигации для иерархических структур в WEB-системах и системах управления WEB-сайтом
Терновая Т.И., Сумская О.П., Слободянюк И.И., Булка Т.И. Контроль качества тканей специального назначения с помощью автоматических систем.
Шеховцов А.В. Інформаційний аспект: розпізнавання образів індивідуума.
Полякова М.В. Определение границ сегмента упорядоченной текстуры на изображении с однородным фоном с помощью многоканального обнаружения пачки импульсов.
Литвиненко В.И. Прогнозирования нестационарных временных рядов с помощью синтезируемых нечетких нейронных сетей
Ковриго Ю.М., Мисак В.Ф., Мовчан А.П., Любицький С.В. Автоматизована система діагностики генераторів електростанцій
Браїловський В.В., Іванчук М.М., Ватаманюк П.П., Танасюк В.С. Керований детектор імпульсного ЯКР спектрометра
Забытовская О.И. Построение функции полезности по экспериментальным данным.
Шиманські З. Апаратні засоби сегментації мовного сигналу
Хобин В.А., Титлова О.А. К вопросу измерения парожидкостного фронта в дефлегматоре абсорбционно-диффузионной холодильной машины (АДХМ)
Фефелов А. А. Использование байесовских сетей для решения задачи поиска места и типа отказа сложной технической системы
Слань Ю. М., Трегуб В. Г. Оперативна нейромережна ідентифікація складних об’єктів керування
Ролик А.И. Модель управления перераспределением ресурсов информационно-телекоммуникационной системы при изменении значимости бизнес-процессов
Кириллов О.Л., Якимчук Г.С., Якимчук С.Г. Изучение электрического поля с помощью датчика измерителя электростатического потенциала на модели замкнутого металлического объема
Грицик В.В. Застосування штучних нейронних мереж при проектуванні комп’ютерного зору.
Гасанов А.С. Информационные технологии построения систем прогнозирования отказов
Шеховцов А.В., Везумский А.К., Середа Е.С. Алгоритм сжатия информации без потерь: модифицированный алгоритм LZ77
Ходаков В.Е., Жарикова М.В., Ляшенко Е.Н. Методы и алгоритмы визуализации пространственных данных на примере моделирования распространения лесных пожаров.
Полторак В.П., Дорогой Я.Ю. Система распознавания образов на базе нечеткого нейронного классификатора.
Литвиненко В.И. Синтез радиально-базисных сетей для решения задачи дистанционного определения концентрации хлорофилла.
Бражник Д.А. Управление совмещением изображения объекта в сцене и эталонного изображения.
Бабак В.П., Пономаренко А.В. Локализация места положения сквозных дефектов по сигналам акустической эмиссии.
Мороз В. В. R-D проблема и эффективность систем сжатия изображений.
Крылов В.Н., Полякова М.В., Волкова Н.П. Контурная сегментация в пространстве гиперболического вейвлет-преобразования с использованием математической морфологии.
Квасников В.П., Баранов А.Г. Анализ влияния дестабилизирующих факторов на работу биканальной координатно-измерительной машины.
Казак В.М., Гальченко С.М., Завгородній С.О. Аналіз можливості застосування імовірнісних методів розпізнавання для виявлення пошкоджень зовнішнього обводу літака.
Тищенко И.А., Лубяный В.З. Управление коммутационными процессами в интегрированных сетях связи.
Корниенко-Мифтахова И.К.,Филоненко С.Ф. Информационно-измерительная система для анализа характеристик динамического поведения конструкций.
Тверезовский В.С., Бараненко Р.В. Модель измерителя емкости с линейной шкалой измерений.
Полякова М.В., Крылов В.Н. Мультифрактальный метод автоматизированного распознавания помех на изображении.
Рожков С.О., Федотова О.М. Алгоритм розпізнавання дефектів тканин для автоматичної системи контролю якості.
Бражник Д.А. Использование проективного преобразования для автоматизации обнаружения объектов.
Ходаков В.Є., Шеховцов А.В., Бараненко Р.В. Математичні аспекти створення автоматизованої системи „Реєстр виборців України”