Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 519.872

АНАЛИЗ СИСТЕМЫ ОБСЛУЖИВАНИЯ С РАЗЛИЧНЫМИ УРОВНЯМИ ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРИОРИТЕТОВ

Пономаренко Л.А., Меликов А.З., Нагиев Ф.Н.

Введение

Приоритеты, определяющие процедуры принятия в буфер (очередь) разнотипных заявок, зачастую называются пространственными приоритетами (Space Priorities, SP), а приоритеты, задающие правила выбора типа заявки из очереди (буфера), получили название временных (Time Priorities, TP). В классических схемах приоритетного обслуживания в системах с очередями, как правило, предполагается, что заявки определенного типа обладают (по сравнению с заявками другого типа) одновременно высокими (или низкими) приоритетами обоих видов.

Вместе с тем, интерес представляют модели обслуживания, в которых заявки одного типа являются чувствительными к возможным потерям из-за переполненности буфера и одновременно не предъявляют жестких требований к потерям, в то время как заявки другого типа, наоборот, не предъявляют жестких требований к потерям, а являются очень чувствительными к возможным задержкам в очереди. Иными словами, целесообразно исследовать модели, в которых заявки одного типа имеют высокие SP и низкие TP, а заявки другого типа, наоборот, имеют низкие SP и высокие TP. Модели такого типа назовем моделями обслуживания с различными уровнями пространственных и временных приоритетов (можно также использовать термин модели обслуживания с множественными приоритетами).

Подобные модели достаточно точно описывают работу узлов сетей коммутации пакетов, в которых пакеты трафика реального времени (например, пакеты речевой информации) имеют высокие ТР и низкие SP по сравнению с пакетами трафика нереального времени (например, пакетами данных), имеющими более высокие SP и низкие TP по сравнению с пакетами реального времени. 

Несмотря на то, что указанные модели представляют большой теоретический и практический интерес, они в доступной литературе не достаточно исследованы. Лишь в последние годы в работах [1-3] исследованы такие модели. При этом в работах [1, 2] используется метод имитационного моделирования, а в работе [3] предлагается аналитический метод для нахождения характеристик системы (вероятностей потерь разнотипных заявок и средних времен их ожидания в очереди). Отметим, что в работе [3] для ожидания заявок с различными требованиями TP используются различные буфера и внутри каждого буфера SP реализуются на основе стратегии вытеснения.

В настоящей работе также исследуется модель с различными уровнями TP и SP. Однако, данная модель отличается от [3] двумя моментами. Во-первых, здесь рассматривается модель с общим буфером для ожидания разнотипных заявок. Во-вторых, для нахождения характеристик модели здесь предлагается численный метод, основанный на принципах теории фазового укрупнения [4]. Использование данного подхода позволяет разработать простые вычислительные процедуры для нахождения искомых характеристик. Ранее данный подход был успешно применен для модели систем со специализированными каналами обслуживания и при наличии лишь пространственных приоритетов различного вида [5-7].

1. Описание модели и расчет ее характеристик

Буферное пространство размера B и канал передачи используются совместно заявками двух типов, при этом заявки первого типа представляют трафик нереального времени, заявки второго типа – трафик реального времени. Используется обычное предположение о пуассоновском характере входящих трафиков, т.е. предполагается, что процесс поступления заявок i-го типа подчиняется закону Пуассона с параметром l_i, =1,2.

Из-за сложности рассматриваемой модели и с целью получения достаточно обозримых результатов здесь предполагается, что для обоих трафиков время обслуживания распределено показательно со средним m^-1. Считается, что заявка любого типа освобождает свое место в буфере в момент выбора ее для обслуживания.

Множественные приоритеты определяются следующим образом. Поскольку трафик первого типа является более чувствительным к возможным потерям пакетов из-за переполненности общего буфера, чем трафик второго типа, то они (т.е. заявки первого типа) имеют высокие пространственные приоритеты. Эти приоритеты осуществляются с помощью стратегии доступа с вытеснением, т.е. поступившая заявка первого типа теряется лишь тогда, когда буфер полностью заполнен и число текущих заявок данного типа в буфере не меньше, чем заданное число с, 1 £ с £ В. Иными словами, поступившая заявка первого типа вытесняет из полностью заполненного буфера заявки второго типа, если текущее число заявок первого типа меньше, чем с; в противном случае, т.е. когда в полностью заполненном буфере число заявок первого типа не меньше чем c, поступившая заявка первого типа теряется. Заявки второго типа теряются тогда, когда буфер полностью заполнен. Параметр  с  назовем пороговым параметром для заявок первого типа.

Замечание 1. При c = B рассматриваемые SP приводят к схеме приоритетизации, исследованной в [3], т.е. введение порогового значения с придает рассматриваемым здесь SP элемент адаптивности.

Поскольку трафик второго типа является более чувствительным к возможным задержкам в очереди, чем трафик первого типа, то заявки второго типа имеют высокие относительные временные приоритеты, т.е. заявки первого типа принимаются для обслуживания лишь тогда, когда в момент освобождения канала в буфере отсутствуют заявки второго типа.

Функционирование буфера описывается двумерной цепью Маркова (а более точно – двумерным процессом рождения и гибели) с состояниями типа n = (n₁, n₂), где n_i указывает число заявок i-го типа в очереди, i = 1,2. Фазовое пространство состояний (ФПС) буфера задается так:

                                                        (1)

Согласно определению введенных множественных приоритетов интенсивности переходов между состояниями n, n¢Î E определяются следующим образом:

                 (2)

где e₁ = (1,0), e₂ = (0,1).

Граф модели показан на рис. 1.

Стационарную вероятность состояния n Î E обозначим через p(n). Тогда, согласно известной теореме PASTA [8] стационарные вероятности потери заявок i-го типа (Call Loss Probability, CLP_i(B,c)),  i=1,2 определяются так:

                                                                       (3)

Здесь E_i – множество блокирующих состояний из ФПС (1)  для  трафика  i-го типа, i = 1,2. При этом под множеством блокирующих состояний для трафика i-го типа понимается множество тех состояний из ФПС E, в которых поступление заявки данного типа означает его потерю безотносительно того, поступает ли в этот момент заявка данного типа или нет.

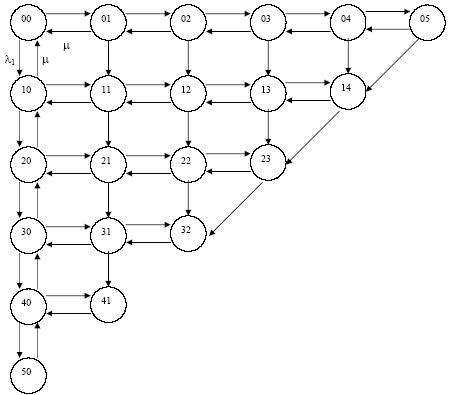
Рис. 1 Граф модели при B = 5, c = 2.

Формально указанные выше множества определяются так:

E₁ = {nÎE₂ : n₁³c};

E₂ = {nÎE: n₁+n₂=B} – множество диагональных состояний.

Отсюда с учетом (3) получаем, что

CLP₁(B, c) < CLP₂(B, c) "cÎ[1, B].

Среднее время задержки в очереди заявок i-го типа (Call Transfer Delay, CTD_i(B,c)) определяется с помощью формулы Литтла для систем обслуживания с конечной очередью:

CTD_i(B, c) := Q_i(B, c)/l_i(1-CLP_i(B, c)),  i = 1,2                               (4)

Здесь Q_i(B,c) обозначает среднее число заявок i-го типа в очереди, i = 1,2. Эти величины определяются так:

                                                      (5)

где E_kⁱ ={nÎE : n_i=k}, i =1,2.

            Следовательно, искомые характеристики модели (3)-(5) определяются через стационарное распределение p(n), nÎE исходной цепи Маркова. С использованием известного критерия Колмогорова для двумерных цепей Маркова [9] можно показать, что для стационарного распределения данной модели не существует мультипликативное решение. Этот факт существенно осложняет проблемы расчета характеристик модели (3)-(5), особенно при больших размерах буфера. Для преодоления этих трудностей предлагается использовать приближенный метод расчета указанных характеристик.

Поскольку предложенный подход достаточно подробно описан в литературе (см., например, [5-7] и библиографию при них), то здесь приводится лишь его краткое изложение применительно к данной модели.

Отметим, что предложенный подход имеет высокую точность и является особенно полезным для расчета стационарного распределения двумерных процессов размножения и гибели, которые являются непрерывными хотя бы по одной компоненте. Напомним, что двумерный процесс размножения и гибели является непрерывным, скажем по первой компоненте, если существует положительные двусторонние вероятности переходов между любыми двумя возможными состояниями типа (i, j) и (i+1, j).

Из соотношений (2) легко видно, что изучаемый двумерный процесс рождения и гибели с ФПС (1) является непрерывным лишь по второй компоненте (см. также рис. 1).

Теперь перейдем к краткому изложению предложенного подхода расчета стационарного распределения изучаемой двумерной цепи Маркова.

            Рассматривается следующее разбиение ФПС E:

            ,                                          (6)

где E_k := E_k¹ (см.(5)).

            Далее классы состояний E_k объединяются в отдельные укрупненные состояния <k> и вводится функция укрупнения на исходном ФПС E:

                                                           (7)

            Функция укрупнения (7) определяет укрупненную цепь Маркова с ФПС

            .                                  

            Стационарное распределение исходной модели определяется так:

                                                           (8)

где  являются стационарными распределениями внутри класса и укрупненной модели, соответственно.

Стационарное распределение внутри класса E_i с учетом (2) определяется как распределение одномерного процесса размножения и гибели:

,                                  (9)

где n₂:=l₂/m (для краткости изложения здесь приводятся формулы лишь для случая n₂¹1).

            Далее на основе (2) и (9) определяется стационарное распределение укрупненной модели:

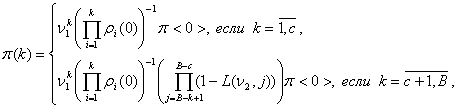               (10)

где

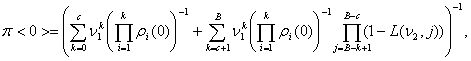                        (11)

n₁=l₁/m,  L(n, k)= n^k(1-n)/(1-n^k+1).

            Тогда, после определенных математических преобразований получим следующие формулы для вычисления искомых характеристик модели:

                                                         (12)

                                                          (13)

                                                                               (14)

                                                                  (15)

Далее, с помощью (12)-(15) вычисляются характеристики (4).

Из формул (9)-(15) видно, что расчет характеристики данной системы обслуживания со сложной схемой приоритетизации сводится к простым вычислительным процедурам. Особенность этих процедур состоит в том, что они подразумевают использование табулированных величин типа L(n, k) (см. также формулы 9).

3. Численные эксперименты по расчету модели

Некоторые результаты численных экспериментов, проведенных с помощью разработанных выше расчетных формул, показаны на рис. 2-13. Во всех экспериментах для простоты принято, что m := 1.

Целью их выполнения является изучение поведения характеристик модели в зависимости от изменения ее параметров (нагрузочных и структурных), а также от порогового параметра для заявок первого типа. Для сравнительного анализа в графиках также показано поведение соответствующих характеристик бесприоритетной модели. Эти характеристики обозначены аналогично приоритетной модели, но только без индексов.

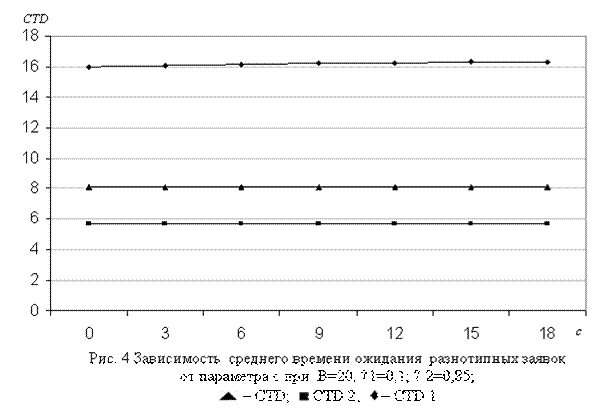
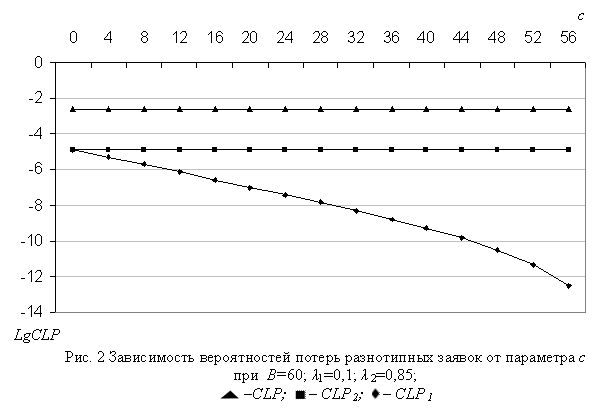
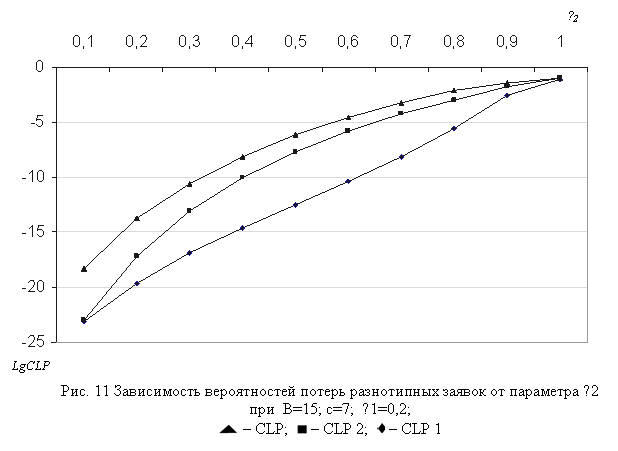
Зависимости характеристик модели от порогового параметра с показаны на рис. 2-4. Как и следовало ожидать, с ростом параметра с шансы для принятия в буфер заявок первого типа растут, и, таким образом, вероятность их потери уменьшается, а одновременно с этим увеличивается вероятность потери пакетов второго типа. При этом скорости их изменения существенным образом зависят от значений параметров модели n₁, n₂ и В (см. рис. 2).

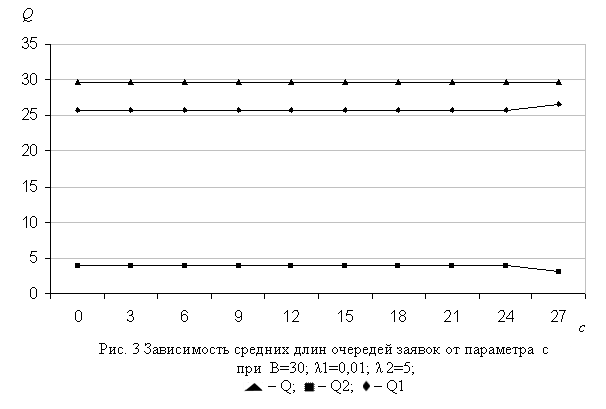
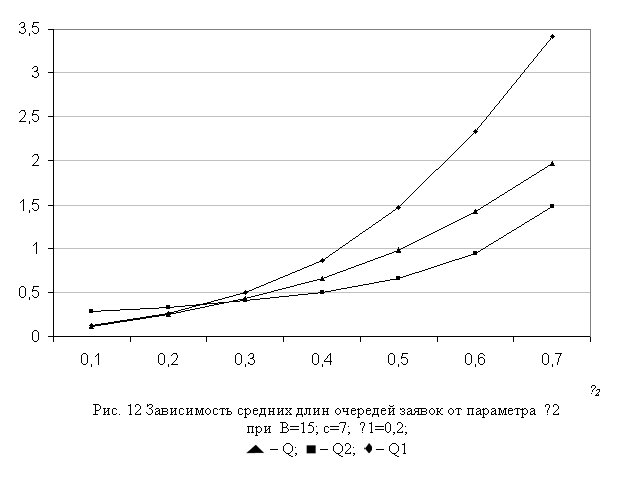
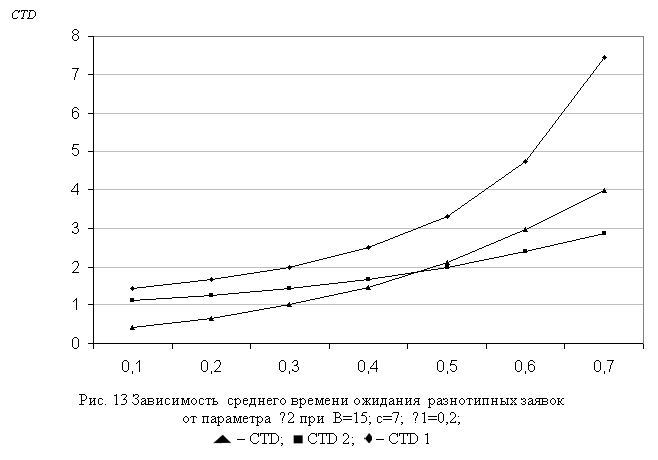
Число заявок первого типа (Q₁) с увеличением параметра с также растет вследствие того, что при этом увеличиваются их шансы попасть в буфер, и одновременно в результате вытеснения из буфера уменьшается число заявок второго типа (Q₂) в буфере (см. рис. 3). Несколько неожиданным оказалось поведение функции CTD₁ от параметра с (рис. 4), т.е. с ростом данного параметра CTD₁ уменьшается. Это объясняется тем, что  при указанных исходных данных с ростом параметра с скорость уменьшения функции CLP₁  во много раз превосходит скорость увеличения функции Q₁ (см. формулы (4)), а CTD₂ при тех же данных является почти постоянной.  

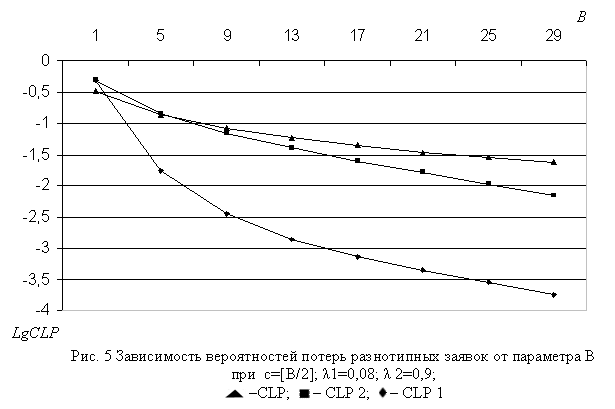
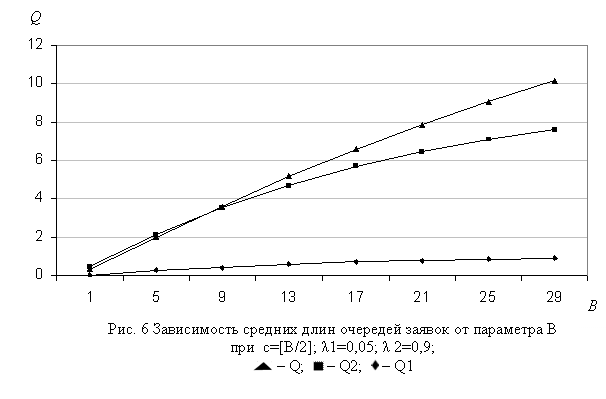
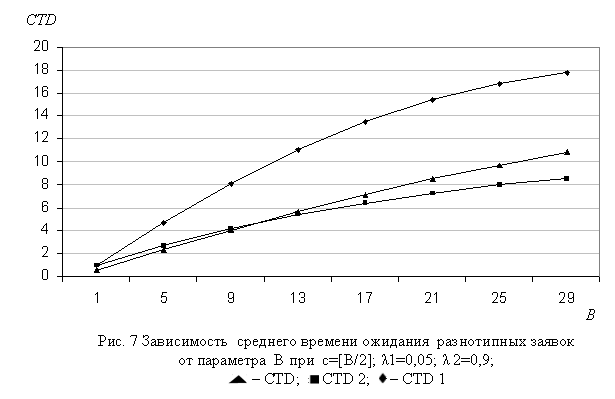
Зависимости характеристик модели от размера буфера (В) показаны на рис. 5-7. Характер этих зависимостей во всех диапазонах изменения исходных данных моделей полностью совпадают с теоретическими ожиданиями, т.е. функции CLP₁ и CLP₂ являются убывающими, а функции Q_k и CTD_k, k = 1,2, наоборот, возрастают относительно аргумента B.    

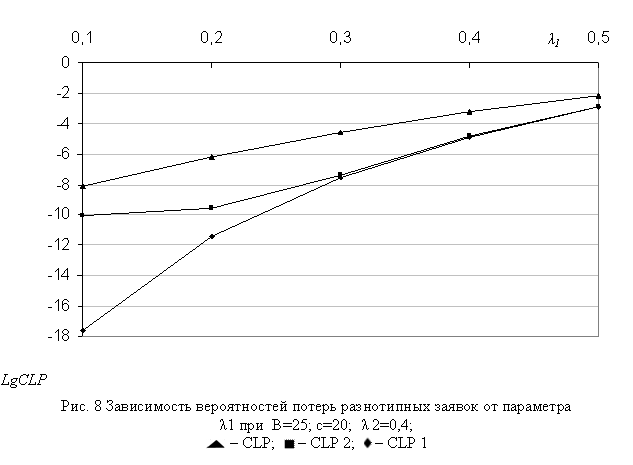
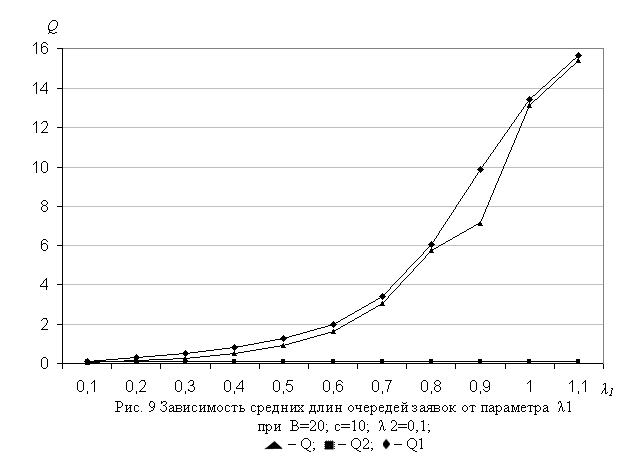
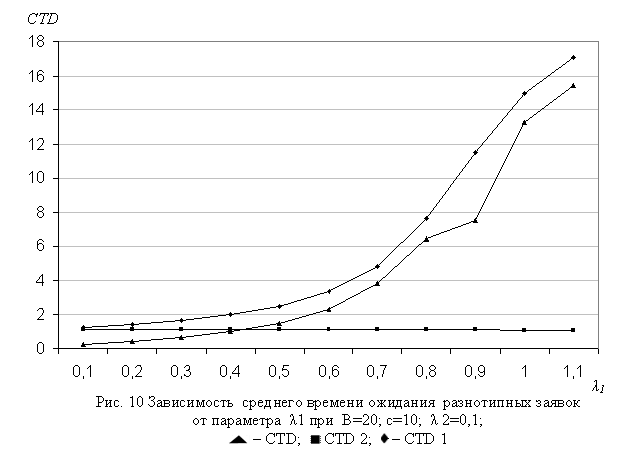
Интерес представляет также изучение зависимости поведения характеристик модели от нагрузки трафиков нереального (l₁) и реального (l₂) времени. Соответствующие трафики показаны на рис. 8-9 и 10-12. Как и следовало ожидать, с ростом нагрузки трафика любого типа все характеристики модели имеют тенденции к возрастанию, при этом скорости их изменения отличаются друг от друга, и существенным образом зависят от исходных данных модели.

 Отметим, что представление в графиках на рис. 2-13 также поведения характеристик бесприоритетной модели позволяют производить сравнительный анализ изучаемых характеристик, и, таким образом, принимать решения относительно целесообразности введения множественных приоритетов. Из представленных графиков видно, что последняя проблема (т.е. принятие решения относительно выбора схемы приоритетизации) не является тривиальной и представляет собой многокритериальную проблему (здесь эти проблемы не рассматриваются).

Заключение

Предложенный в данной работе подход предлагает достаточно простые алгоритмы расчета характеристик модели обслуживания со сложной схемой приоритетизации разнотипных трафиков, представляющих различные требования к возможным потерям и задержкам в очереди. Разработанные алгоритмы могут быть использованы и для выбора оптимальных (в заданном смысле) параметров модели с целью достижения искомых значений исследуемых характеристик. Эти задачи представляют собой предмет специальных исследований.

1.                  Chao H.J., Peckan I.H. Queue management with multiple delay and loss priorities for ATM switches // Proc. ICC’94. – 1994. – P.1184 – 1189.

2.                  Shan Zhi C., Liemin Y. A new priority control of ATM output buffer // Telecommunication Systems. – 1995. – № 4. – P. 61 – 69.

3.                  Lee Y., Choi B.D. Queueing system with multiple delay and loss priorities for ATM networks // Information Systems. – 2001. – № 138. – P. 7 – 29.

4.                  Королюк В.С. Стохастические модели систем. – К.: Наук. думка, 1989. – 208 с.

5.                  Меликов А.З., Фаттахова М.И., Нагиев Ф.Н. Подход фазового укрупнения для оптимизации стратегий доступа с вытеснением в сетях коммутации пакетов // Кибернетика и системный анализ. – 2004. – № 2. – С.107 – 115.

6.                  Пономаренко Л.А., Меликов А.З., Фаттахова М.И. Стратегия вытеснения с виртуальным порогом для доступа в буфер узла интегральной сети // Проблемы управления и информатики. – 2004. – № 4. – С. 106 – 115.

7.                  Пономаренко Л.А., Меликов А.З., Фаттахова М.И. Численные методы исследования многопотоковых систем обслуживания с виртуальным разделением буфера // Кибернетика и системный анализ. – 2004. – № 6. – С. 168 – 172.

8.                  Wolff R.W. Poisson arrivals see time averages // Oper. Res. – 1992. – 30, № 2. – P. 223 – 231.

9.                  Kelly F.P. Reversibility and stochastic networks. – London.: John Wiley & Sons, 1979. – 230 p.