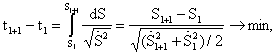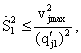УДК 517.9
ИСПОЛЬЗОВАНИЕ МЕТОДА ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ БЕЛЛМАНА В ЗАДАЧАХ ОПТИМИЗАЦИИ БЫСТРОДЕЙСТВИЯ МАНИПУЛЯТОРА
Рудакова А.В., Кузик О.В.
Введение
В последние годы в различных отраслях промышленности для интенсификации производства стали применяться гибкие производственные системы. Наиболее важной технологической компонентой такого интегрированного производства является манипуляционный робот, представляющий собой сложный пространственный механизм с несколькими степенями свободы, содержащий жесткие и упругие звенья, передачи и приводы, который является единой динамической системой, требующей оптимального управления. Оптимальный закон управления манипулятором можно получить, задав функционал максимального быстродействия и решив обратную задачу кинематики.
Постановка задачи
Задача максимального быстродействия задается следующим образом. Необходимо переместить захват манипулятора из начального состояния в конечное за минимальное время, с учетом существующих ограничений на обобщенные скорости и ускорения. Считается, что в начальном и конечном состояниях скорости звеньев манипулятора равны нулю.
Функционал максимального быстродействия задается в виде
|
|
(1) |
или
|
|
|
где tl и tl+1 – время перехода манипулятора в l-ое и в l+1-ое промежуточные состояния; Sl, Sl+1 – значение обобщенной координаты в l-ом и в l+1-ом состояниях; l – точка на траектории захвата.
Ограничения, накладываемые на обобщенные скорости и ускорения, имеют вид:
|
|
(2) |
|
|
(3) |
где
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() - обобщенные скорости и ускорения в в l-ой и в l+1-ой точке траектории движения захвата манипулятора.
- обобщенные скорости и ускорения в в l-ой и в l+1-ой точке траектории движения захвата манипулятора.
В крайних точках манипулятор покоится, следовательно
|
|
(4) |
Таким образом, ![]() следует выбирать таким, чтобы выполнялись условия (2) – (4) и при этом время перемещения (1) было минимальным.
следует выбирать таким, чтобы выполнялись условия (2) – (4) и при этом время перемещения (1) было минимальным.
Решение задачи
Поставленная задача достаточно сложна, так как у манипулятора есть ещё ограничения на обобщенные координаты qj. Следовательно, прежде чем решать задачу оптимизации, нужно определить L-1 промежуточных состояний, для которых определить последовательность векторов x0, x1, … , xL, через которые следует провести траекторию движения, и обобщенные координаты qjl.
В качестве исходных данных для расчета оптимальных движений манипулятора используются матрицы, определяющие расположение оборудования относительно системы координат, связанной с манипулятором; матрицы, определяющие расположение детали на оборудовании; «векторы подхода», задающие направления возможных движений в рабочей зоне станка при загрузке-разгрузке; ограничения на точки траектории, обусловленные геометрической формой станков; ограничения на обобщенные координаты манипулятора; кинематическая и динамическая модели манипулятора; ограничения на число опорных точек; начальная и конечная точки движения манипулятора.
Обобщенные координаты в начале интервала l, то есть в момент времени t0, известны. Для момента t1 найдем обобщенные координаты при помощи метода последовательных приближений, который заключается в следующем: в нулевом приближении обобщенным координатам ![]() ,
, ![]() , … ,
, … , ![]() задают произвольные значения, значения обобщенных координат в первом приближении
задают произвольные значения, значения обобщенных координат в первом приближении ![]() ,
, ![]() , … ,
, … , ![]() находят из системы уравнений
находят из системы уравнений
|
|
(5) |
где ![]() - vμ-тый элемент матрицы Tn, равной произведению матриц перехода Ai (i =1..n).
- vμ-тый элемент матрицы Tn, равной произведению матриц перехода Ai (i =1..n).
Матрицы перехода Ai составляются из матриц элементарных перемещений (вращения и сдвига)
|
Ai = Bвр(k,Qi)Bсд(k,Si)Bсд(i,ai)Bвр(i,αi), |
(6) |
![]() - vμ-тый элемент матрицы Uij=dTi/dqj. Матрицы элементарных перемещений имеют вид
- vμ-тый элемент матрицы Uij=dTi/dqj. Матрицы элементарных перемещений имеют вид
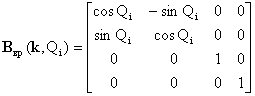 ,
, 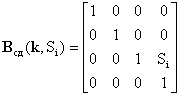 ,
,
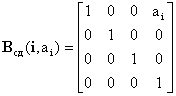 ,
, 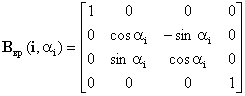 .
.
Так как приближенные значения ![]() известны, то из системы (5) определяются уточненные значения
известны, то из системы (5) определяются уточненные значения ![]() . Итерационная процедура вычислений продолжается до тех пор, пока разность
. Итерационная процедура вычислений продолжается до тех пор, пока разность![]() не становится меньше наперед заданной малой величины ε. При расчете на ЭВМ необходимо следить за тем как велико число итераций, обеспечивающих заданную точность. Если траектория проходит близко от особой точки, в которой сливаются два решения, то число итераций будет возрастать. В этом случае для уменьшения объема вычислений целесообразно уменьшить расчетный шаг по траектории. Одновременно, плохая сходимость итераций – свидетельство того, что траектория выбрана неудачно и манипулятор может работать неустойчиво.
не становится меньше наперед заданной малой величины ε. При расчете на ЭВМ необходимо следить за тем как велико число итераций, обеспечивающих заданную точность. Если траектория проходит близко от особой точки, в которой сливаются два решения, то число итераций будет возрастать. В этом случае для уменьшения объема вычислений целесообразно уменьшить расчетный шаг по траектории. Одновременно, плохая сходимость итераций – свидетельство того, что траектория выбрана неудачно и манипулятор может работать неустойчиво.
Расчеты показывают, что самой оптимальной траекторией движения манипулятора между двумя точками является прямая. Если из-за внешних препятствий движение по прямой организовать невозможно, то траекторию движения необходимо разбить на ряд прямолинейных отрезков, соединяющих опорные точки движения. При решении данной задачи необходимо учитывать геометрию технологического оборудования и тип технологической оснастки, предусмотреть возможность разного захвата детали, применять метод матриц четвертого порядка, использовать как кинематическую, так и динамическую модель манипулятора.
Задача поиска опорных точек решается с помощью моделирования на ЭВМ процесса движения манипулятора на основе кинематической и динамической модели механизма манипулятора.
Задача о наилучшем выборе величины ![]() решается методом динамического программирования. Выбирается параметр точности решения ε – шаг изменения величины
решается методом динамического программирования. Выбирается параметр точности решения ε – шаг изменения величины![]() ; последовательно рассматриваются интервалы (Sl, Sl+1), начиная с последнего (l = L-1). На каждом интервале табулируются две функции
; последовательно рассматриваются интервалы (Sl, Sl+1), начиная с последнего (l = L-1). На каждом интервале табулируются две функции ![]() и
и ![]() , причем величина
, причем величина ![]() в таблицах меняется с шагом ε. Считается, что функция
в таблицах меняется с шагом ε. Считается, что функция ![]() уже известна. Величина τl – это минимальное время, за которое манипулятор можно перевести из точки Sl в конечное состояние, выполнив условия (2-4), если в точке Sl задана скорость
уже известна. Величина τl – это минимальное время, за которое манипулятор можно перевести из точки Sl в конечное состояние, выполнив условия (2-4), если в точке Sl задана скорость ![]() . Величина
. Величина ![]() - это значение
- это значение ![]() при оптимальном движении манипулятора, обеспечивающем его приход в конечное состояние за время τl. Для последнего интервала, где
при оптимальном движении манипулятора, обеспечивающем его приход в конечное состояние за время τl. Для последнего интервала, где ![]() не может иметь, согласно (4), никаких значений кроме 0, и τl(0) = 0. Таблицы для l<L строятся следующим образом: Аргумент
не может иметь, согласно (4), никаких значений кроме 0, и τl(0) = 0. Таблицы для l<L строятся следующим образом: Аргумент ![]() последовательно увеличивается с шагом ε, начиная от нулевого значения. При каждом значении
последовательно увеличивается с шагом ε, начиная от нулевого значения. При каждом значении ![]() в таблицу τl записывается вначале очень большое значение τl, далее, просматривается таблица для функции
в таблицу τl записывается вначале очень большое значение τl, далее, просматривается таблица для функции ![]() и для каждой точки этой таблицы проверяется выполнение неравенств (2-3). Если
и для каждой точки этой таблицы проверяется выполнение неравенств (2-3). Если ![]() и
и ![]() равно нулю, то все неравенства выполняются. При очень большом значении
равно нулю, то все неравенства выполняются. При очень большом значении ![]() неравенства не выполняются ни при каких значениях
неравенства не выполняются ни при каких значениях ![]() .
.
Пусть для некоторой пары ![]() ,
, ![]() неравенства выполнены. Тогда вычисляется
неравенства выполнены. Тогда вычисляется
|
|
(7) |
Полученные значения сравниваются с ранее записанными в таблицу τl значениями ![]() . Если новое значение
. Если новое значение ![]() меньше старого, оно заносится в таблицу, иначе там сохраняется старое значение. Если таблица τl – обновляется, то одновременно в таблицу
меньше старого, оно заносится в таблицу, иначе там сохраняется старое значение. Если таблица τl – обновляется, то одновременно в таблицу![]() заносится значение
заносится значение ![]() , для которого величина
, для которого величина ![]() оказалась менее найденной прежде. В итоге после просмотра всей таблицы
оказалась менее найденной прежде. В итоге после просмотра всей таблицы ![]() для точки
для точки ![]() находится минимальное значение τl и одновременно наилучшее значение
находится минимальное значение τl и одновременно наилучшее значение ![]() , при котором этот минимум достигается.
, при котором этот минимум достигается.
Табулирование ![]() и
и ![]() требует конечного числа операций. Производя расчеты по всем значениям l, можно построить таблицу
требует конечного числа операций. Производя расчеты по всем значениям l, можно построить таблицу ![]() , из которой нам нужна только одна точка (при
, из которой нам нужна только одна точка (при ![]() ), то есть
), то есть ![]() - минимальное время, за которое покоящийся в точке
- минимальное время, за которое покоящийся в точке![]() манипулятор можно перевести в точку
манипулятор можно перевести в точку ![]() , подойдя к этой точке в нулевой скоростью. Чтобы узнать, как изменяется скорость
, подойдя к этой точке в нулевой скоростью. Чтобы узнать, как изменяется скорость ![]() вдоль траектории, последовательно просматривают интервалы (Sl, Sl+1), начиная с первого, для которого l =0. В начале каждого интервала
вдоль траектории, последовательно просматривают интервалы (Sl, Sl+1), начиная с первого, для которого l =0. В начале каждого интервала![]() - известная величина (на первом интервале она равна нулю). Для этого известного значения
- известная величина (на первом интервале она равна нулю). Для этого известного значения ![]() выбирается из таблицы
выбирается из таблицы ![]() наилучшее значение
наилучшее значение ![]() и берется следующий интервал. Так последовательно находятся все наилучшие значения
и берется следующий интервал. Так последовательно находятся все наилучшие значения![]() , обеспечивающие быстродействие.
, обеспечивающие быстродействие.
Заключение
Исходя из вышеизложенного, можно сделать вывод, что, если ввести сильные ограничения на скорость и ускорение одной обобщенной координаты qi и слабые ограничения по прочим обобщенным координатам, то оптимальный закон движения слагается из трех этапов, связанных с qi: разгон с предельным ускорением ![]() , движение с предельной скоростью
, движение с предельной скоростью ![]() , предельное гашение скорости с замедлением
, предельное гашение скорости с замедлением ![]() . Если ужесточить ограничения на скорость и ускорение по прочим обобщенным координатам, то характер определения оптимального движения усложняется:
. Если ужесточить ограничения на скорость и ускорение по прочим обобщенным координатам, то характер определения оптимального движения усложняется:
1 этап – разгон с предельным для q3 ускорением ![]() ;
;
2 этап – движение с предельной для q1 скоростью ![]() ;
;
3 этап – гашение скорости с предельным замедлением ![]() .
.
Таким образом, оптимальные законы движения компонуются из интервалов, на каждом из которых одно из ограничений (на ![]() или
или ![]() ) для какой-то одной из обобщенных координат становятся действующими (соответствующее неравенство превращается в равенство).
) для какой-то одной из обобщенных координат становятся действующими (соответствующее неравенство превращается в равенство).
|
In the article are brought prospects of use numerical methods and theories of matrixes for deciding the problems of kinematics of manipulation robotics. Offered method of determination of general coordinates, velocities and speedups of sections of manipulator on given motion paths. Stated Bellman’s method of dynamics programming adapted for deciding the problems of optimal control of moving a manipulator. |
1. Вукобратович М., Стокич Д. Управление манипуляционными роботами: Теория и приложения. – М.: Наука, 1985.
2. Галиуллин А.С. Обратные задачи динамики. – М.: Наука, 1981.
3. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования. – М.: Машиностроение, 1989.
4. Динамическое управление роботами. /Под ред. Е.И. Юревича. – М.: Наука,1984.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.