УДК 004.627

Введение. Количество информации необходимой человечеству в повседневной работе неуклонно растет. Объемы устройств, для хранения данных и пропускная способность линий связи также растут. Однако, количество информации растет намного быстрее. Данная проблема может быть решена 3 способами.

Первый – ограничение количества информации. К сожалению, он не всегда приемлем. Например, для изображений это означает уменьшение разрешения, что приведет к потере мелких деталей и может сделать изображения вообще бесполезными (например, для медицинских или космических изображений).

Второй – увеличение объема носителей информации и пропускной способности каналов связи. Это решение связано с материальными затратами, причем иногда весьма значительными.

Третий способ – использование сжатия информации. Этот способ позволяет в несколько раз сократить требования к объему устройства хранения данных и пропускной способности каналов связи без дополнительных издержек (за исключением издержек на реализацию алгоритмов сжатия). Условиями его применимости является избы­точность информации и возможность установки специального програм­много обеспечения либо аппаратуры как вблизи источника, так и вблизи приемника информации. Как правило, оба эти условия удовлетворяются.

Первые теоретические разработки в области сжатия информации относятся к концу 40-х годов. В конце семидесятых появились работы Шеннона, Фано и Хафмана.

Необходимость сжатия информации в вычислительных сетях вытекает из того, что пропускная способность каналов связи более дорогостоящий ресурс, чем дисковое пространство, по этой причине сжатие данных до или во время их передачи очень актуально.

Здесь целью сжатия информации является экономия пропускной способности и в конечном итоге ее увеличение.

Все известные алгоритмы сжатия сводятся к шифрованию входной информации, а принимающая сторона выполняет дешифровку принятых данных.

Существуют методы, которые предполагают некоторые потери исходных данных, другие алгоритмы позволяют преобразовать информацию без потерь.

— Сжатие с потерями используется при передаче звуковой или графической информации, при этом учитывается несовершенство органов слуха и зрения, которые не замечают некоторого ухудшения качества, связанного с этими потерями.

— Сжатие информации без потерь осуществляется статистическим кодированием или на основе предварительно созданного словаря. Статистические алгоритмы (напр., схема кодирования Хафмана) присваивают каждому входному символу определенный код. При этом, наиболее часто используемому символу присваивается наиболее короткий код, а наиболее редкому - более длинный. Таблицы кодирования создаются заранее и имеют ограниченный размер. Этот алгоритм обеспечивает наибольшее быстродействие и наименьшие задержки. Для получения высоких коэффициентов сжатия статистический метод требует больших объемов памяти.

Постановка задачи. Известны основные типы избыточности, которые перечислил в своей работе Т. Вел­ч [1]:

а) избыточность распределения событий (разные события имеют разные вероятности);

б) избыточность повторения событий (несколько одинаковых событий могут следовать друг за другом);

в) избыточность цепочек событий (цепочки событий могут повторяться);

г) позиционная избыточность – повышение вероятности появления определенных событий в некоторых позициях потока событий (например, в записях базы данных).

Приведенная классификация составлена в 1984 г. и практически не устарела, однако нуждается в некоторых дополнениях.

В представленной работе предлагается математическая модель, которая учитывает дополнительные условия избыточности и на основе существующего алгоритма сжатия текстовой информации без потерь разрабатывается новый алгоритм [1].

Дополнение 1. Классификация ориентирована в первую очередь на символьные источники информации. Нетекстовым источникам данных характерны свои виды избыточности. Например, графическим данным характерна пространственная избыточность, характеризующаяся высокой вероятностью близости не только значений соседних пикселей, но и их пространственных производных.

 Дополнение 2. Избыточность цепочек событий может быть представлена альтернативным способом – как избыточность распре­деления событий после наступления некоторого количества непосред­ственно предшествующих событий. Практические реализации, основанные на таком подходе, обеспечивают заметно более высокую степень сжатия, чем просто устраняющие цепочечную избыточность.

Для начала рассмотрим метод группового кодирования: подавление нулей. Это один из старейших способов, который исключал избыточность типа б, упоминавшейся ранее. В данном методе текст сканируется на наличие повторяющихся символов. Если количество повторяющихся символов было более 3, то алгоритм заменял данную строку двухсимвольным кодом.

Пример: строка XYZbbbbbQRA заменялась на следующую строку — XYZSc5QRA.

Однако данный алгоритм имеет ряд недостатков. Один из наиболее важных недостатков — способность данного алгоритма устранять избыточность лишь одного типа символов. В факсимильной связи к примеру, это недостатком не является, что видно из рис. 1: присутствуют лишь чёрные и белые пиксели.

Рис. 1 

Следующим шагом будет рассмотрение метода группового кодирования, исключающего недостатки предыдущего метода, в котором напомню, происходило подавление избыточности лишь одного типа символов. Данный алгоритм предлагает заменять повторения трёхсимвольным кодом. На рис. 2 иллюстрируется применение данного метода к символьным данным. Здесь используются следующие обозначения:

Sc — специальный символ, указывающий на то, что за ним следуют сжатые данные;

Х — любой повторяющийся символ;

Сс — счётчик символов, то есть количество повторений сжатого символа.   

Рис. 2  Формат сжатия при групповом кодировании

Примеры сжатия при групповом кодировании приведены в таблице 1.

Таблица 1

Таким образом, данный метод позволяет сократить место, занимаемое любой последовательностью из четырёх и более одинаковых символов.

Рассмотрим алгоритм LZ77. Пусть имеется следующая бессмыслен­ная фраза: the brown fox jumped over the brown foxy jumping frog. Длина этой фразы 53 байта, то есть 424 бита.

Алгоритм обрабатывает этот текст слева направо. Вначале каждый символ преобразуется в 9-битовый код, состоящий из двоичной единицы, за которой следует 8-битовое ASCII-представление символа. Во время обработки текста алгоритм ищет повторяющиеся последовательности.

Когда встречается повторяющаяся последовательность, алгоритм ищет конец такой последовательности, то есть каждый раз алгоритм отыскивает как можно больше символов. Первой такой последовательностью является the brown fox. Повторяю­щаяся последовательность заменяется указателем на первый экземпляр последо­вательности и длиной этой последовательности. В данном случае последователь­ность the brown fox встречается на 26 позиций раньше и имеет длину 13 символов. Для данного примера рассмотрим два варианта кодирования: 8-битовый указатель и 4-битовая длина или 12-битовый указатель и 6-битовая длина. При этом 2-бито­вый заголовок указывает, который вариант выбран: 00 означает первый вариант, а 01 — второй вариант. Таким образом, второй экземпляр последовательности the brown fox кодируется как <00b>,<26d><13d> или 00 00011010 1101.

Оставшиеся части сжатого сообщения представляют собой букву у, последова­тельность <00b><27d|><5d|>, заменяющую последовательность, состоящую из про­бела, за которым следует строка jump, и последовательность символов ing frog.

На рис. 3 иллюстрируется преобразование алгоритма сжатия. Сжатое со­общение состоит из 35 9-битовых символов и двух кодов, то есть всего из 35 • 9 + + 2 • 14 = 343 бит. Таким образом, при 424 бит в несжатом сообщении коэффици­ент сжатия данного метода в этом примере составил 1,24.

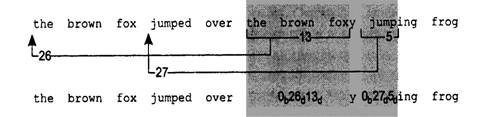
Рис. 3  Пример работы метода LZ77

Основная концепция. В процессе совершенствования существующих алгоритмов сжатия данных без потерь было обосновано выведено, что если отдельные кодируемые символы встречаются в исходном тексте с вероятностью Pi, то в лучшем случае мы можем использовать для каждого символа код длины Li, удовлетворяющей следующему неравенству:

Здесь Pi представляет собой вероятность, с которой i-ый символ встречается в исходных данных, а Li — длину двоичного кода, которым кодируется данный символ. Исходя из неравенства (1) можно показать, что:

Здесь Н(Х) представляет собой энтропию множества символов Х, а Е[L] является средней длиной кода для множества Х. В схеме сжатия без потерь Н(Х) всегда будет нижней границей объёма сжатых данных, так как Н(Х) определяет среднее количество информации, содержащейся в символьном наборе.

Согласно дополнению 2, приведённом в данной работе, эффективность алгоритма сжатия данных может быть повышена путём объединения символов и одновременного кодирования блоков по К символов каждый. В результате получаем следующее неравенство:

Таким образом, существует способ повышения эффективности алгоритма сжатия. Если нам нужно отправить сообщение длинной в N символов, мы можем использовать блок длинной N символов. Таким образом, мы обращаемся с каждым сообщением как с одним из MN возможных результатов, где М представляет собой количество атомарных символов, а N — длину сообщения.     

Решение поставленной задачи.  Как уже было оговорено ранее, эффективность алгоритма сжатия данных может быть повышена путём объединения символов и одновременного кодирования блоков по К символов каждый.

Пусть дан нам следующий текст: “ABCABEFJAB”, который состоит из 10 символов, а это в свою очередь 10 байт или 80 бит.

Алгоритм LZ77 предположим кодирует 1 способом: весь текст преобразуется в 9-битовый код, за которой следует 8 битовое ASCII-представление представление, а остальные кодированные блоки преобразует в 14 битовый код, состоящий из: 2 бит заголовка, 8 битового указателя и 4 битовой длины.

Итого, для данного текста общий размер будет: 6*9+2*14=82 бита, что на 2 бита больше незакодированного сообщения.

Заархивировав данное сообщение с помощью архиватора WinRar версии 7,0 beta 2, получил следующие результаты, смотри рис. 4. Как видно из рисунка, размер сжатого сообщения вышел 79 байт, что составляет 632 бита. 

Рис. 4  Сжатие исходного текста с помощью WinRar

Теперь рассмотрим предложенный алгоритм, модифицированный метод сжатия LZ77.  Здесь весь текст преобразуется в 9-битовый код, за которым следует 8 битовое ASCII-представление символа.

Закодированный текст будет выглядить так:

Как видно, перед каждым символом, добавлен бит: 0 — символ незакодирован, а 1 — символ закодирован. Обозначение <02d> означает число 02 в десятичном коде. После небольших манипуляций, получим 2 числа (0 и 2), где:

0 — позиция начла блока;

2 — количество символов в блоке.

Таким образом, мы получим 8 символов по 9 бит каждый, это 72 бита на весь текст. Исходя из полученного результата, степень сжатия для такого столь малого текста составляет 1,1111. Делая вывод, можно сказать, что полученный модифицированный алгоритм позволяет получить наилучшие показатели степени сжатия для малых текстов.

Однако, даже на этом этапе, можно обнаружить недостаток синтезированного алгоритма — максимальный показатель счётчика будет равен 9, и максимальное значение символов в блоке также будет равно 9.

Решить данную проблему можно следующим путём: преобразуем в 9-битовый код весь текст, за которым следует 8 битовое ASCII-представление символа. Теперь кодирование будет представляться следующим форматом: <x><y><z>, где:

<x> — это 1 бит указывающий кодирован символ или нет;

<y> — указывающий, какой вариант кодирования используется (I или II); 

<z> — закодированный символ.

            Отличия II вариант от I не особенно значительны, за исключением того, что все символы перекодируются в 9-битовый код, размер кода составит 12 бит, что позволяет нам использовать уже 99 позиций для смещения счётчика и 9 символов в блоке.

            Для проверки работоспособности данного алгоритма и сравнения его работы, рассмотрим пример, когда передаётся сообщение по факсимильной связи. Пусть дана следующая последовательность, представленная в таблице 2.

Таблица 2.

Исходная последовательность

Закодируем данную последовательность с помощью алгоритма LZ77, причём будем кодировать блоками по 3 символа и только нули. В результате мы получим: 24 блока по 3 символа, и 19 символов преобразованных в 9-битный код. В результате мы получим: 24*14+19*9=336+171=507 бит, степень сжатия при этом будет составлять 1.5779

Рассмотрим работу представленного алгоритма. Результатом кодирования в первом случае будет: (24+19)*9=387 бит, а степень сжатия будет 2,0671. Во втором варианте кодирования  результат будет следующий: (24*12)+(19*9)=288+171=459 бита, а степень сжатия в данном случае будет равной 1,7429.

Этот же тип данных, сжатый с помощью оговоренного ранее программного обеспечения WinRAR в результате получил размер, равный 102 байтам, что в свою очредь составляет 816 бит, что намного больше размера исходных данных.

Заключение. Необходимо учитывать, что при устранении одних видов избыточности, другие виды избыточности, присущие тому же потоку событий, могут исчезать (например, после устранения в потоке символов избыточности типа “а” устранить другие типы избыточности не представляется возможным) или сохраняться (например, при устранении избыточности типа “б” может сохраняться избыточность типа “а”, хотя ее характеристики несколько меняются). Кроме того, в выходном потоке при устранении определенных видов избыточности могут появляться новые виды избыточности.

Учитывая новые условия избыточности, был предложен модифицированный алгоритм сжатия данных без потерь на основе уже существующего алгоритма LZ77. Экспериментальные исследования наглядно продемонстрировали эффективность модифицированного алгоритма.

Использование данного алгоритма позволит достичь более высоких результатов сжатия информации передаваемой в факсимильной связи, а тем самым, сократить время для передачи сообщения и расходы при междугородней и международной связи.

1.                  Современные компьютерные сети. 2-3 изд. / В. Столингс.—СПб.:Питер, 2003.—783с.

2.                  Теория вероятностей и математическая статистика / В.Е. Гмурман— М.: Высш. шк., 2000.—250с.