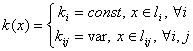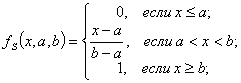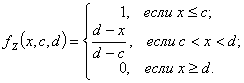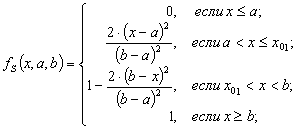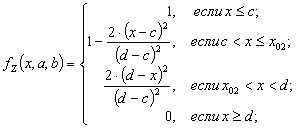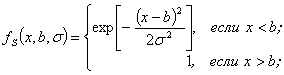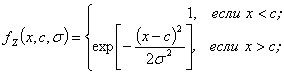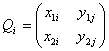УДК 519.711.3
ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ ДЛЯ МОДЕЛИРОВАНИЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕННЫХ ОБЪЕКТОВ
Шейник С.П., Рудакова А.В.
Постановка проблемы. При оперативном управлении распределенными объектами операторами часто приходиться оценивать диспетчерам параметры состояния объектов, которые зависят не только от времени, но и от пространственных координат. Для этого необходимо наличие модели, которая учитывает территориальное изменение коэффициентов, используемых для описания динамического поведения распределенных объектов.
Анализ последних достижений и публикаций. Современные технологические комплексы представляют собой интеграцию множества территориально распределенных объектов и систем управления. Задачи оценивания текущего состояния таких систем и определение оптимального управления представляют значительную трудность, что приводит к недопустимым затратам времени при оперативном управлении [1,2].
Функционирование распределенных объектов можно моделировать с помощью поверхностей (непрерывных оболочек) аппроксимируя значения различных параметров (например, тип почв (способность почв впитывать воду, поступающую с поверхности) (рис.1 а); тип выращиваемых культур (количество воды, расходуемое растениями на создание единицы урожая основной продукции) (рис.1 б) ) по всей области существования объекта [3].
|
а) по типу почв |
б) по виду культур |
|
Рис.1 Классификация орошаемой территории. |
|
Для учета изменений различных коэффициентов в зависимости от пространственных координат в поверхностной модели можно использовать функции принадлежности.
Целью статьи является исследование возможности применения функций принадлежности для моделирования учета различных коэффициентов в пространственно распределенных объектах.
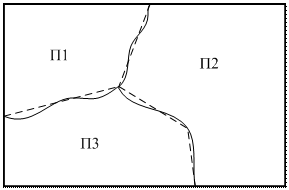
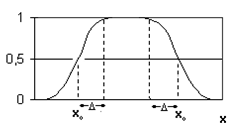
Основная часть. Любой пространственный коэффициент k(x), зависящий от одной координаты х и принимающий различные значения на разных участках можно представить в виде одномерной функции (рис.2).
На графике k(x), изображенном на рис.2, можно выделить области постоянства значений ki и переходные участки kij:
|
|
(1) |
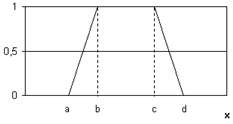
Построим модель изменения коэффициентов при следующих допущениях:
- существуют области постоянства значений li;
- границы областей плотно примыкают друг к другу;
- существуют переходные участки lij, где коэффициенты изменяются плавно (линейно);
- границы проходят через центры переходных участков, и значения коэффициентов на границе определяются как среднее арифметическое значение коэффициентов смежных зон;
- размеры всех переходных зон одинаковы l12=l23=l34=2Δ.
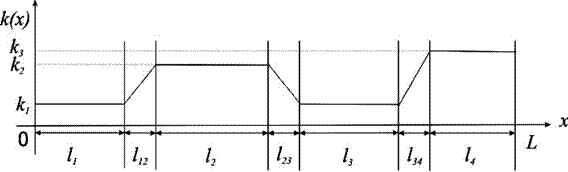
Рис. 2. График изменения коэффициента по координате х
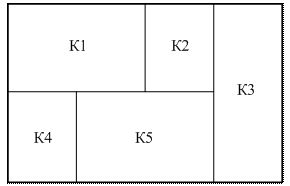
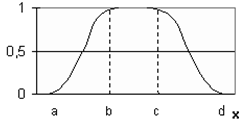
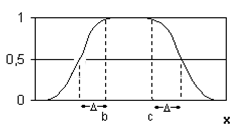
Таким образом, для удобства моделирования параметров распределенного объекта с учетом принятых допущений введем ряд дополнительных обозначений (рис.3):
|
|
(2) |
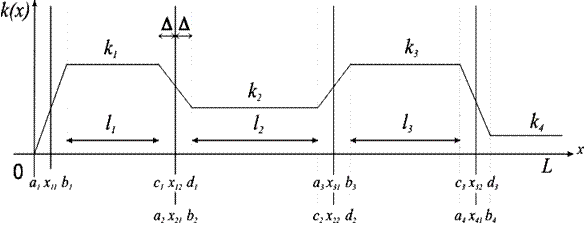
Рис. 3. Геометрическое соответствие описания распределенных областей
Для формирования зависимостей ![]() целесообразно использовать функции принадлежности Π-образного вида [4], которые можно также получить на основе S и Z-образных функций принадлежности по формуле:
целесообразно использовать функции принадлежности Π-образного вида [4], которые можно также получить на основе S и Z-образных функций принадлежности по формуле:
|
|
(3) |
Типовые функции принадлежности S и Z-типа являются: трапециевидная, сплайн-функция, гауссова и сигмоидная. Функции принадлежности для описания переходных участков с учетом принятых допущений и обозначений (2) можно задать следующим образом:
Функции принадлежности трапециевидной формы:
|
S-образная
|
Z-образная
|
(4) |
Сплайн-функции принадлежности:
|
S-образная
|
Z-образная
|
(5) |
где ![]() - центр левой границы;
- центр левой границы; ![]() - центр правой границы.
- центр правой границы.
Гауссовы функции принадлежности:
|
S-образная
|
Z-образная
|
(6) |
где ![]() - коэффициент концентрации;
- коэффициент концентрации; ![]() - размер переходных участков.
- размер переходных участков.
Сигмоидные функции принадлежности:
|
S-образная
|
Z-образная
|
(7) |
где ![]() - коэффициент крутизны;
- коэффициент крутизны; ![]() – допустимая ошибка;
– допустимая ошибка; ![]() ,
,![]() - центры левого и правого переходных участков соответственно.
- центры левого и правого переходных участков соответственно.
Графики соответствующих П-образных функций принадлежности, полученных на основе S и Z-образных функций по выражению (3) приведены на рис.4.
|
а) трапециевидная |
б) сплайн-функция |
|
в) гауссова |
г) сигмоидная |
Рис. 4. Функции принадлежности
Модель пространственно изменяемого коэффициента будем формировать следующим образом:
|
|
(8) |
где n – количество областей; ki – значение коэффициента; ![]() - П-образная функция принадлежности для і-области.
- П-образная функция принадлежности для і-области.
С точки зрения программной реализации наиболее простыми оказались сигмоидные функции принадлежности, для формирования которых не требуется проверки граничных условий (отсутствуют логические операции).
Моделирование графика изменения пространственного коэффициента k(x) проводилось при следующих исходных данных: количество смежных участков – ![]() ; вектор координат центров переходных участков (четких границ между областями) -
; вектор координат центров переходных участков (четких границ между областями) - ![]() ; вектор значений коэффициентов в областях постоянства -
; вектор значений коэффициентов в областях постоянства - ![]() ; характерный размер переходных участков -
; характерный размер переходных участков - ![]() ; допустимое отклонение значений коэффициентов в точках стыковых переходных участков и областей постоянства параметров -
; допустимое отклонение значений коэффициентов в точках стыковых переходных участков и областей постоянства параметров - ![]() .
.
Результаты моделирования функций принадлежности и пространственного коэффициента ![]() приведены на рис.5.
приведены на рис.5.
Аналогичным образом можно при моделировании учитывать разнообразные коэффициенты в территориально распределенных объектах, которые зависят от двух координат ![]() .
.
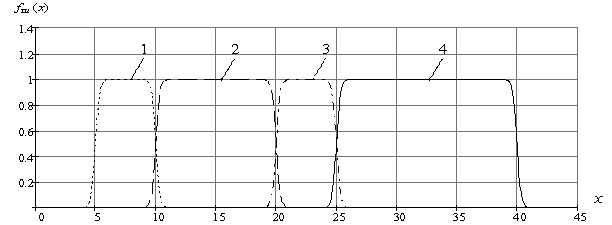
а) сигмоидные П-образные функции принадлежности ![]() для каждого участка:
для каждого участка:
1 – ![]() ; 2 –
; 2 – ![]() ; 3 –
; 3 – ![]() ; 4 –
; 4 – ![]() .
.
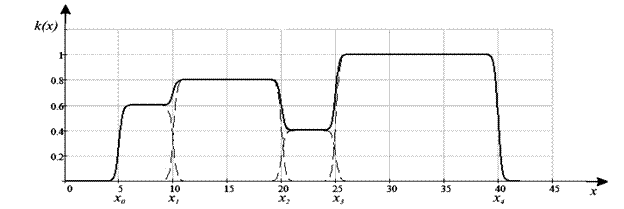 б) пространственный коэффициент k(x):
б) пространственный коэффициент k(x):
Рис.5. Результат моделирования зависимости k(x).
В этом случае П-образные пространственные функции принадлежности можно получить перемножением П-образных функций принадлежности по соответствующим координатам:
|
|
(9) |
где функции ![]() и
и ![]() формируются по выражениям (3).
формируются по выражениям (3).
Модель пространственного коэффициента ![]() изменяющегося по двум координатам запишется аналогично (8) в виде:
изменяющегося по двум координатам запишется аналогично (8) в виде:
|
|
(10) |
где ![]() - количество областей;
- количество областей; ![]() - значение коэффициента;
- значение коэффициента; ![]() - П-образная функция принадлежности для i-области с координатами
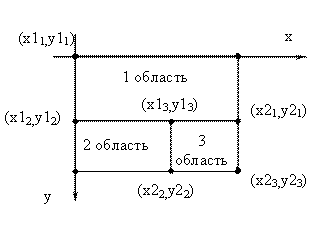
- П-образная функция принадлежности для i-области с координатами![]() . Расположение характерных координат для задания i-области прямоугольной формы можно представить в виде матрицы
. Расположение характерных координат для задания i-области прямоугольной формы можно представить в виде матрицы
|
|
(11) |
где ![]() - координаты левого верхнего угла;
- координаты левого верхнего угла; ![]() - координаты правого нижнего угла.
- координаты правого нижнего угла.
Моделирование изменения пространственного коэффициента ![]() проводилось при следующих исходных данных: количество смежных областей –
проводилось при следующих исходных данных: количество смежных областей – ![]() ; матрица характерных координат областей -,
; матрица характерных координат областей -, ![]() ,
, ![]() ,
, ![]() ; вектор значений коэффициентов в областях постоянства -
; вектор значений коэффициентов в областях постоянства - ![]() ; характерный размер переходных участков -
; характерный размер переходных участков - ![]() ; допустимое отклонение значений коэффициентов в точках стыковых переходных участков и областей постоянства параметров -
; допустимое отклонение значений коэффициентов в точках стыковых переходных участков и областей постоянства параметров - ![]() .
.
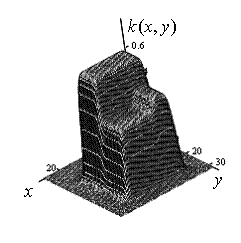
Результаты моделирования пространственного коэффициента ![]() для рассматриваемого разделения на области постоянства (рис.6а) приведены на рис. 6б.
для рассматриваемого разделения на области постоянства (рис.6а) приведены на рис. 6б.
|
|
|
|
а) графическое представление областей |
б) пространственный коэффициент |
Рис.6. Результаты моделирования зависимости ![]()
Выводы. Для моделирования учета различных значений коэффициентов в распределенных объектах можно использовать функции принадлежности П-типа, которые формируются из S и Z-образных функций принадлежности, соответствующих границам (переходным участкам) между отдельными областями.
Наиболее простыми по алгоритму реализации являются сигмоидные функции. Для формирования непрерывной аппроксимирующей функции k(x) достаточно задать характерные параметры областей хi, размеры переходных участков Δ и допустимую ошибку ![]() .
.
Рассмотренный подход можно применить при моделировании территориально распределенных объектов ![]() и для областей произвольной формы с использованием аффинных или полиномиальных преобразований.
и для областей произвольной формы с использованием аффинных или полиномиальных преобразований.
ЛИТЕРАТУРА:
1. Методы робастного, нейро-нечеткого и адаптивного управления./Под ред., Н.Д.Егупова. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2002. – 744с.
2. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1978.
3. Поливода О.В., Шейник С.П., Рудакова А.В. Использование непрерывных оболочек для моделирования влагосодержания почвы//Вестник Херсонского национального технического университета. – 2009. - №2(35). – С.357-362.
4. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПБ.:БВХ-Петербург, 2003. – 736с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.