УДК 66.063.94
МАТЕМАТИЧНА МОДЕЛЬ ТА АЛГОРИТМ ЕКСТРЕМАЛЬНОГО УПРАВЛІННЯ ПРОЦЕСОМ ОСАДЖЕННЯ ДИСПЕРСНОЇ ФАЗИ СУСПЕНЗІЇ
Шпильовий Л.В.
Підвищення ефективності функціонування радіального згущувача на збагачувальних фабриках за рахунок вдосконалення системи автоматичного управління є досить актуальним. Особливої актуальності це питання набирає сьогодні, з огляду на необхідність інтенсифікації всіх збагачувальних процесів, в тому числі згущення, через постійне зниження якості руди, що залучається до переробки, та необхідність забезпечення зростання обсягів виробництва. Необхідність вдосконалення існуючих САУ процесом згущення зумовлена також вимогами економії реагентів (флокулянтів), а також підвищеною увагою до стану забруднення навколишнього середовища зливами згущувачів.
Спроби інтенсифікувати процес згущення за рахунок більш ефективного автоматичного дозування флокулянту в радіальний згущувач відомі давно [1–3]. Так, в [1] пропонувалося флокулянт подавати в залежності від масових витрат дисперсної фази в суспензії живлення згущувача, що мало б забезпечити наперед визначені оптимальні питомі витрати флокулянту, за яких швидкість осадження частинок дисперсної фази була б максимальною. В роботах [2,3] автоматичне дозування флокулянта пропонується здійснювати за допомогою систем регулювання замкненого типу. При цьому в якості вихідного параметру процесу пропонуються посередні показники – мутність зливу [2], чи висота зони проясненої рідини у згущувачі [3]. Останні САР мають ту перевагу, що реагують на всі можливі збурення процесу згущення. Але через велику інерційність об'єкту, особливо на згущувачах великого діаметра, якість автоматичного регулювання та ефективність застосування флокулянтів і в цих випадках залишається незадовільною [4]. Невідповідність сучасного стану автоматизації дозування флокулянтів в процесах згущення вимогам практики зневоднення концентратів та продуктів збагачення корисних копалин пояснюється недостатньою дослідженністю основних закономірностей процесу осадження дисперсної фази зфлокульованих суспензій та відсутністю математичних моделей, придатних для побудови ефективних алгоритмів управління.
Сучасний рівень вивченості механізму флокуляції хоч і дає якісну характеристику процесу, та не дає кількісних залежностей, які для конкретного типу промислової суспензії характеризували б вплив основних технологічних її параметрів на швидкість осадження дисперсної фази; дозволяли визначити раціональні режими процесу і розрахувати оптимальні витрати флокулянту, за яких забезпечується найвища швидкість осадження. При недостатньому дозуванні флокулянту не відбувається злипання частинок в агрегати через малу товщину покриття поверхні частинок дисперсної фази; при передозуванні флокуляція не відбувається через стабілізацію суспензії. Звичайно оптимальні витрати флокулянту визначають в залежності від витрат дисперсної фази суспензії живлення згущувача. Але відомо, що ступінь флокуляції суттєво залежить від електрокінетичного потенціалу на поверхні частинок дисперсної фази, який визначається концентрацією іонів водню в рідкій фазі суспензії [5]. Тому вибір флокулянту та його витрат має бути узгодженим з мінералогічним та гранулометричним складом дисперсної фази, а також іонним складом рідкої фази суспензії. Цей вибір може бути обґрунтований лабораторними дослідами осадження суспензій.
Тож невирішеним залишається вивчення умов та визначення раціональних режимів осадження дисперсної фази за спільного та одночасного впливу основних параметрів процесу на швидкість падіння зфлокульованих частинок, встановлення характеру залежності, розробка математичної моделі, придатної для цілей управління, та алгоритму оптимального управління процесом згущення.
Метою статті є розробка регресійної моделі процесу осадження польовошпатового концентрату та алгоритму управління автоматичним дозуванням флокулянту в радіальний згущувач.
Завдання вирішували шляхом дослідження впливу найбільш важливих параметрів процесу осадження, які визначалася попередніми нашими дослідженнями різних типів промислових суспензій [6,7] та аналізом відомих аналітичних залежностей [8], на швидкість осадження дисперсної фази.
Осадження є визначальною стадією для всього процесу згущення [9]. Зростання швидкості осадження частинок дисперсної фази призводить до зросту продуктивності згущувача по твердому і зливу без зниження якості зливу. При стабільних параметрах живлення менше частинок дисперсної фази виноситься висхідними потоками рідини в злив згущувача.
З огляду на відому залежність продуктивності згущувача від швидкості осадження метою управління режимом осаджування в радіальному згущувачі має бути автоматична підтримка максимального значення швидкості осадження дисперсної фази: w → тах.
Об’єктом дослідження були штучні суспензії, які готували з сухих порошків лежалих хвостів колишньої збагачувальної фабрики, що переробляла руду Маріупольського цирконового родовища. Мінералогічний склад польовошпатового концентрату, мас. доля, % : мікроклін – 44,0; альбіт – 34,4; нефелін – 20,55; егірин – 0,3; лепідомелан – 0,32; циркон – 0,05; пірохлор – 0,01; гідроокисли заліза – 0,22; інші – 0,15.
Хімічний склад концентрату відповідав технічним вимогам технологічного регламенту на виробництво польовошпатового концентрату, мас. доля, % : K2O – 6…7; Na2O – 5…6; SiO2 – 60…65; Fe2O3 – 0,15…0,25; Al2O3 – 20…22; ZrO2 – 0,04; Nb2O5 – 0,03; TiO2 – 0,1.
Питома маса концентрату – 2,60…2,62 г/см3.
Дослідження проводили методом активного експерименту в лабораторних умовах за відомою методикою [10] в скляному циліндрі ємністю 500 см3.
При плануванні експерименту за незалежні фактори приймали: Qф – питомі витрати флокулянту, визначені як об'ємні витрати флокулянту на одиницю загальної поверхні одиниці маси дисперсної фази суспензії, ![]() ; рН – концентрація іонів водню, од.; C – концентрація дисперсної фази в суспензії, %; d – вміст класу – 0,063 мм в дисперсній фазі, %; t – температура суспензії, 0С.
; рН – концентрація іонів водню, од.; C – концентрація дисперсної фази в суспензії, %; d – вміст класу – 0,063 мм в дисперсній фазі, %; t – температура суспензії, 0С.
Величину рН суспензії доводили до завданого значення розчином соди (Na2CO3). Як флокулянт застосовували 0,1 %-ий водний розчин поліакриламіду (ПАА), який вводили в скляний циліндр піпеткою.
В якості цільової функції (Y, мм/с) прийнято швидкість осадження, яка визначалася згідно загальноприйнятих рекомендацій [10]. При проведенні експерименту слідкували за опусканням межі розподілу фаз в циліндрі. Час, за який межа розподілу фаз досягала контрольної позначки на шкалі циліндра, реєстрували за допомогою секундоміра. Швидкість осадження визначали за зміною часу проходження межею розподілу фаз контрольної позначки.
Експеримент поставлено за програмою центрального композиційного ротатабельного плану другого порядку Бокса-Хантера [11]. Ядро плану представлено напівреплікою 25-1 (1=Х1Х2Х3Х4Х5). Реалізовані 16 дослідів на основних рівнях доповнені ще 10 дослідами в зіркових точках (величина зіркового плеча в цьому випадку дорівнює 2) та шістьома дослідами в центрі плану.
Основні рівні, інтервали варіювання факторів та межі області дослідження вибрані за результатами попередніх експериментів і на основі апріорної інформації (табл. 1).
Область зміни незалежних факторів відповідає допустимому технологічним регламентом діапазону зміни технологічних параметрів.
Функція відгуків апроксимована поліномом другого порядку. Обробка результатів експерименту та аналіз регресійної моделі здійснено за допомогою модуля „Планування експерименту” статистичної програми Statgraphics 3.0 Plus.
Значущість коефіцієнтів моделі визначалася за допомогою Р-рівня і наведено на стандартизованому Парето-графіку (рис.1). Вертикальна лінія на рис.1 відповідає 95 % статистичній значущості коефіцієнтів.
Рівняння регресії з урахуванням значущості коефіцієнтів отримало вигляд:
Y = 7,286 + 0,579 X1 − 0,129 X2 − 0,588 X3 − 0,775 X4 + 0,554 X5 −
0,571 X12 + 0,681 X1 X2 − 0,590 X22 (1)
Коефіцієнти моделі наведено в нормованому (кодованому) виді.
Таблиця 1
Основні рівні, інтервали варіювання факторів та межі області дослідження
|
Параметр
|
Позначення
|
Код
|
Одиниця виміру |
Інтервал
|
Основні рівні |
||||
|
+2 |
+1 |
0 |
-1 |
-2 |
|||||
|
Витрати флокулянту |
Qф |
Х1 |
|
0,05 |
0,20 |
0,15 |
0,10 |
0,05 |
0,00 |
|
Концентрація іонів водню |
рН |
Х2 |
од. |
0,80 |
10,0 |
9,20 |
8,40 |
7,60 |
6,80 |
|
Вміст класу -0,063 мм в дисперсній фазі |
d |
Х3 |
% |
5,00 |
100,0 |
95,0 |
90,0 |
85,0 |
80,0 |
|
Концентрація дисперсної фази в суспензії |
C |
Х4 |
% |
5,00 |
30,0 |
25,0 |
20,0 |
15,0 |
10,0 |
|
Температура суспензії |
t |
Х5 |
оС |
5,00 |
26,0 |
21,0 |
16,0 |
11,0 |
6,00 |
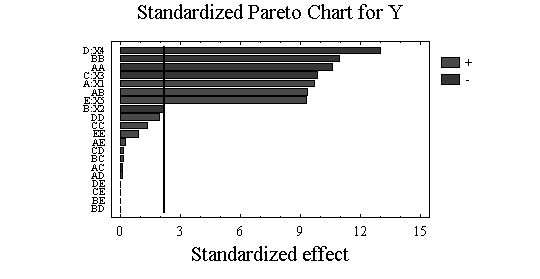
Рис. 1 Значущість коефіцієнтів моделі (Парето-графік)
Як видно з Парето – графіка, статистично значущими є коефіцієнти при лінійних членах рівняння регресії, коефіцієнти при X12 та X22, та коефіцієнт при парній взаємодії членів X1 та X2.
Значення коефіцієнтів регресії в рівнянні (1) визначають силу впливу відповідних факторів чи їх комбінацій на величину функції відгуку, а знак перед коефіцієнтом – характер цього впливу. Як бачимо, на швидкість осадження дисперсної фази найбільше впливають концентрація дисперсної фази в суспензії, питомі витрати флокулянту та концентрація іонів водню в суспензії. Але треба враховувати, що фактори Х1 та Х2 входять до рівняння у вигляді квадратичних членів, що призводить до заниження їх впливу на функцію відгуку при оцінці за величиною коефіцієнтів регресії. Порівняння розрахункових та експериментальних даних швидкості осадження дисперсної фази показало, що різниця між ними мінімальна (стандартна похибка σ = 0,28 мм/с), що свідчить про адекватність моделі. Останнє підтверджується також високим значенням коефіцієнту детермінації R-квадрат, який складав 97,80 %.
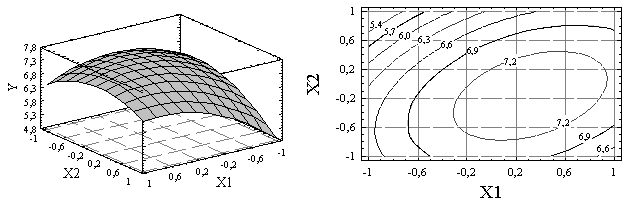
Аналіз регресійної моделі здійснено за допомогою згаданої статистичної програми «Statgraphics 3.0 Plus». На рис. 2 наведено найбільш характерну тривимірну поверхню функції відгуку та її перетини. Зупинимося на них докладніше.
Як видно з рис. 2,а поверхня відгуку Y = f(X1,X2) – це еліптичний параболоїд з екстремумом-максимумом в області Х1 = 0,35; Х2 = – 0,1 (в кодованому вигляді). Екстремальна залежність швидкості осадження від витрат флокулянту може бути пояснена тим, що при недостатніх витратах ПАА на поверхні частинок твердої фази утворюється плівка флокулянту замалої товщини, а при передозуванні флокулянту наступає стабілізація суспензії [13].
а) б)
Рис. 2 Поверхня Y = f (X1,X2) – (а), та її контурні криві – (б) при Х3=Х4=Х5=0
Екстремальний характер залежності швидкості осадження від величини рН середовища пов’язаний, на нашу думку, із загальновизнаним механізмом дії електроліту на подвійний електричний шар (ПЕШ) на поверхні частинок.
Перетини поверхні відгуку Y = f(X1,X2) при середніх (нульових) значеннях інших змінних процесу наведено на рис. 2,б.
Аналіз рівняння (1) показує, що зміни таких факторів, як вміст класу – 0,063 мм в дисперсній фазі суспензії, концентрація дисперсної фази в суспензії живлення, та температура суспензії призводять до зміни швидкості осадження, але не до дрейфу координат екстремуму питомих витрат флокулянту.
Перевірка регресійної залежності (1) в промислових умовах, яка полягала в порівнянні результатів спостережень за величиною швидкості осадження дисперсної фази суспензії в промисловому згущувачі з результатами розрахованих значень швидкості за моделлю, показала достатню збіжність (похибка 10,9 %).
На рис. 3 наведені одномірні залежності функції відгуку від питомих витрат флокулянту за різної концентрації іонів водню в дисперсійному середовищі. Як видно з рисунка, при застосуванні флокулянту швидкість осаджування дисперсної фази збільшується приблизно в 2…5 разів. Але ефективність дії флокулянту суттєво змінюється в залежності від того, в якому за іонним складом дисперсійному середовищі відбувається процес флокуляції. Зміна концентрації іонів водню в суспензії від –2 (рН = 6,8) до +2 (рН = 10,0) призводить до зміни швидкості осадження. Характер залежності при цьому істотно змінюється: відхилення величини рН середовища від оптимального призводить до зниження ефективності дії флокулянту, тобто швидкості осадження. Координати екстремуму змінюються при цьому як по осі ординат, так і по осі абсцис.
Причину такого впливу концентрації іонів водню на ефективність дії флокулянту автори роботи [12] вбачають в тому, що спочатку, із збільшенням рН, спостерігається стиснення дифузної частинки ПЕШ за рахунок переходу протиіонів у внутрішню обкладинку. Це, очевидно, полегшує закріплення і флокулюючу дію реагента. Подальше збільшення рН супроводжується перезарядкою поверхні частинки. При цьому умови закріплення реагенту погіршуються і ефект флокуляції дещо знижується.
Таким чином, координати оптимуму питомих витрат флокулянту, за яких досягається найвища швидкість осадження дисперсної фази, можуть змінюватися в залежності від іонного складу рідкої фази суспензії - дисперсійного середовища, - що має враховуватися при автоматизації режиму осадження в радіальному згущувачі.
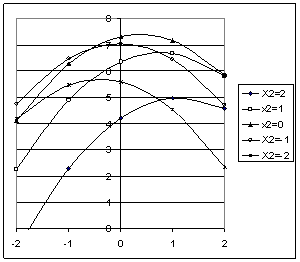
Рис. 3 Залежність швидкості осадження польовошпатового концентрату від питомих витрат флокулянту Х1 та величини рН суспензії Х2
Знаходження оптимальних щодо показників якості значень керуючих впливів і підтримку оптимального режиму при безперервній зміні зовнішніх збурень, що призводять до зміщення координат точки екстремуму, можна здійснити за допомогою системи екстремального управління. Вирішити екстремальну задачу управління можна, використовуючи принцип управління за збуренням, так як існує можливість безперервного контролю основного збурення (величини рН), яке змінює положення точки екстремуму, та встановлено характер впливу цього збурення на зміну режимів роботи системи. В цьому випадку можна створити розімкнений функціональний зв’язок за збуренням, за допомогою якого робота системи в оптимальних режимах буде забезпечуватися з відповідною точністю. Велика інерційність радіального згущувача та труднощі, пов’язані з контролем вихідних показників якості (абсолютної швидкості осадження), а також відносна простота вимірювання величини рН, дозволяють рекомендувати застосування екстремальної системи розімкненого типу з компаундним зв’язком за збуреннями [13].
Екстремальна задача управління режимом осадження дисперсної фази в радіальному згущувачі зводиться до підтримки максимуму швидкості осадження w (показник екстремуму) при існуючій концентрації іонів водню в дисперсійному середовищі рН (збурення) за допомогою зміни питомих витрат флокулянта Qф (керуючий вплив). При такому способі управління показник екстремуму (w) не вимірюється і тому задача екстремального управління вирішується за допомогою жорсткого функціонального зв'язку між збуренням рН і керуючим впливом Qф: Qфопт = f (рН).
Отримавши інформацію про збурення необхідно на основі апріорних даних про властивості об'єкту знайти оптимальні управління. Залежність оптимальних керуючих впливів від збурень Qфопт = f (рН) при зміні останніх може визначатися різними способами, але найбільш економічний полягає в виконанні на моделі попередніх розрахунків, згортці результатів в функції чи таблиці, і використання останніх для управління [14].
При зміні величини рН суспензії необхідно коригувати питомі витрати флокулянту таким чином, щоб швидкість осадження залишалися максимальною. Для побудови алгоритму управління необхідно знати залежність оптимальних питомих витрат флокулянту від величини рН дисперсного середовища. Для цього з статичних характеристик, наведених на рис. 3, для різних значень концентрації іонів водню в робочому діапазоні її зміни визначали величину питомих витрат флокулянту (Qфопт), за яких швидкість осадження дисперсної фази досягає максимального значення. Значення інших факторів (густина суспензії живлення, вміст класу – 0,063 мм в дисперсній фазі, температура) в цих розрахунках приймалися сталими і рівними середнім значенням.
Обробка результатів розрахунків методом найменших квадратів за допомогою пакету Statgraphics 3.0 Рlus дозволила побудувати залежність оптимальних питомих витрат флокулянту від концентрації іонів водню (в кодованому вигляді), яку можна виразити лінійним рівнянням виду:
Qфопт = 0,42 рН + 0,4 (2)
Рівняння (2) є оптимальною характеристикою компаундування, якій притаманна та властивість, що всім точкам, що лежать на ній, відповідає максимальна швидкість осадження при фіксованих значеннях концентрації іонів водню.
При суттєвій зміні коефіцієнтів моделі, наприклад внаслідок зміни мінералогічного складу руди, розрахунок і згортка результатів повторюються. В цьому випадку при управлінні проводяться лише прості розрахунки за залежностями Qфопт = f (рН). Завдяки цьому контролер може бути звільнений від постійного пошуку оптимальних значень управляючих впливів за моделлю. Він може бути зайнятий роботою по корекції моделі, перевірці її адекватності, знаходженню рівнянь виду Qфопт = f (рН) при зміні коефіцієнтів моделі, та рішенню цих рівнянь.
Вимірюючи збурення і визначаючи за формулою (2) керуючі впливи, з врахуванням обмежень 0 ≤ Qфопт ≤ Qфмах можна управляти процесом осадження дисперсної фази оптимально з точки зору вибраного критерію ефективності, та з точністю, що відповідає частці контрольованого збурення в формуванні критерію ефективності.
Висновки. Дослідження процесу осадження, як об’єкту автоматичного управління показало, що існує екстремальна залежність швидкості осадження дисперсної фази суспензії польовошпатового концентрату від питомих витрат флокулянту і концентрації іонів водню в дисперсійному середовищі. Застосування екстремального управління є необхідною умовою підвищення ефективності роботи промислових згущувачів на збагачувальних фабриках. Таке управління можна реалізувати екстремальною системою розімкненого типу. Розроблена регресійна математична модель адекватно описує процес осадження польовошпатових хвостів збагачення рідкіснометалічних руд Маріупольського цирконового родовища. Модель застосована для визначення оптимальних режимів та розробки алгоритму оптимального управління процесом осадження суспензії у радіальному згущувачі.
In work it is developed and analysed regressional model of process of sedimentation of a dispersive phase of tails of enrichment cyrcon ores of the Mariupol deposit, and it is offered algorithm of extreme management of batching flowculantsв in a densifier1.
1. Стальский В. В. Автоматизация управления процессами обезвоживания на обогатительных фабриках. - М.: Недра, 1977. – 200 с.
2. Автоматизация производства на углеобогатительных фабриках / Л. Г. Мелькумов, В. А. Ульшин, М. А. Бастунский и др. - М.: Недра, 1983. - 295 с.
3. Головков Б. Ю., Колпиков Г. Г., Рейбман Л. А. Автоматизация калийных обогатительных фабрик. - М.: Недра, 1983. - 200 с.
4. Папушин Ю.Л., Самойлов А.И. К вопросу автоматического управления процессом сгущения отходов флотации / Наукові праці Дон. держ.техн. універ. Вип. 42, серія гірничо-електромеханічна. - Донецьк: Дон ДТУ, 2002. – С.187 - 191.
4. Небера В.П. Флокуляция минеральных суспензий. - М.: Недра, 1983. - 288 с.
5. Білецький В.С., Шпильовий Л.В. Оптимізація режиму осадження твердої фази у згущувачі // Складні системи і процеси. – 2002, №2. – с. 78 – 82.
6. Шпильовий Л.В., Білецький В.С., Сергєєв П.В. Математичне моделювання процесу осадження твердої фази хвостів флотації рідкісно-металічних руд // Вісник Криворізького технічного університету. Вип. 3.: Зб. наук. пр. - Кривий Ріг: КТУ, 2004.
7. Кизевальтер Б.В. Теоретические основы гравитационных процессов обогащения. – М.: Недра, 1979. – 295 с.
8. Справочник по обогащению руд. Специальные и вспомогательные процессы / Под ред. Богданова О.С., Ненарокомова Ю.Ф., 2-е изд., перераб. и доп. - М.: Недра, 1984. - 358 с.
9. Руководство к практическим заняттям в лаборатории процессов и аппаратов химической технологи. /Под ред. чл..-корр. АН СССР П. Г. Романкова – 6-е изд., перераб. и доп. – Л.: Химия, 1990. – 272 с.
10. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической
11. технологии. – 2-е изд., перераб. и доп. – М.: Высш. шк.., 1985. – 327с.
12. Барбин М.Б. О влиянии ПАВ и рН среды на отстаивание и фильтрование // Изв. ВУЗ. - Цветные металлы. - 1993, № 3-4. – с. 2 - 4
13. Пат. №65879 А Україна, МКВ3 В 01D 21/00. Спосіб автоматичного керування процесом осадження твердої фази / Шпильовий Л.В., Білецький В.С.; Заяв. 01.09.03; Опубл. 15.04.04, Бюл. № 4. – 2 с.
14. Барский Л. А., Козин В. С. Системный анализ в обогащении полезных ископаемых. – М.: Недра, 1977. – 486 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.