УДК 004.02:681.3
МОДЕЛЬ АВТОМАТИЗОВАНОЇ СИСТЕМИ УПРАВЛІННЯ ПОТОКАМИ ТРАНСПОРТНИХ ЗАСОБІВ
Славич В.П.
Постановка проблеми. Постійне збільшення кількості транспортних засобів призводить до перевантаженості доріг, росту транспортних затримок та появі тривалих пробок. Невпинне зростання інтенсивностей транспортного руху викликає необхідність в розробці методів, спрямованих на збільшення пропускних можливостей дорожньої мережі та зменшення відповідних наслідків існуючих транспортних проблем.
Сучасний розв’язок транспортних труднощів полягає в організації автоматизованого управління дорожнім рухом та розробці відповідної бази. Важливою складовою такої автоматизованої системи управління транспортними потоками є інформаційно-математичні методи і моделі, що забезпечують раціональне управління об’єктом транспортної мережі. Завдяки отриманню інформації про параметри потоку в реальному часі, а також враховуючи статистичні параметри процесу, подібна модель використовуються для формування керуючих дій, що передаються на засоби дорожньої сигналізації [1, 2] та безпосередньо впливають на транспортний потік.
Аналіз існуючих методів управління транспортною системою дає висновок, що всі подібні моделі мають два основні недоліки. Перший недолік – це спрощеність моделі, другий – вузьке застосування. Отже, розв’язок, запропонований ними, має невелике практичне значення [3-7].
В зв’язку з цим виникає задача розробки методів управління потоками автомобілів, які б забезпечували прийнятний результат.
Сучасним напрямком побудови подібних моделей є використання апарату нечітких множин та нечіткої логіки [8,9]. Необхідність використання нечіткої теорії обумовлено невизначеністю інформації на перехресті про потік транспортних засобів.
Мета дослідження. Розробка моделі управління режимами роботи світлофорної сигналізації на основі апарату нечіткої логіки, що дозволяє вибирати оптимальні варіанти регулювання з найменшим перебуванням транспортних засобів у системі.
Основний матеріал. Для системи управління потоком транспортних засобів на базі нечіткої логіки використаємо, структуру, що ображено на рис.1.
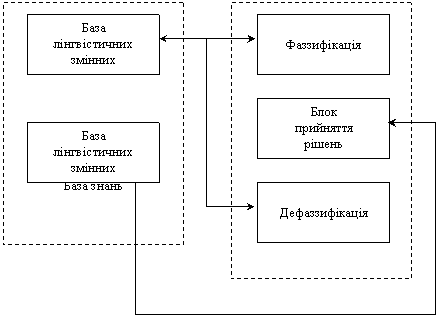 |
Рис.1 Структура системи управління транспортним потоком
Нехай задано систему перехресть (рис.2). Для синхронної роботи світлофорів необхідно, щоб тривалості циклу кожного з них були однакові. Проміжки часу між початками циклів світлофорів двох прилеглих перехресть є час синхронізації tс.
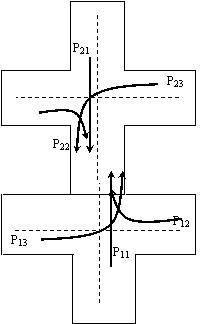 |
Рис. 2 Схема транспортних потоків на двох перехрестях
Система управління потоком транспортних засобів (СУПТЗ) буде регулювати управління tс так, щоб мінімізувати наступну суму часу очікування автомобілів:
![]() , (1)
, (1)
де tij – час очікування автомобілів потоку Pij, ![]() .
.
В запропонованій СУПТЗ в якості вхідних лінгвістичних змінних є наступні:
1) tо – поточний час синхронізації;
2) kij – кількість автомобілів, що проїде на зелений сигнал у напрямку Pij, ![]() .
.
Вихідною лінгвістичною змінною буде Dtс – зміна часу синхронізації tс.
Система має для певного набору значень величин kij видавати таке значення Dtс, яке змінює tс, наближаючи його до оптимального значення tопт.
База правил заповнюється наступним чином:
1. Для заданих значень kij визначається таке значення tопт, при якому tо приймає найменше значення.
2. Визначається, при якому Dtс значення виразу
![]() , (2)
, (2)
буде ближче до оптимального tопт за допомогою наступної системи:
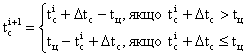 , (3)
, (3)
де tц – тривалість циклу світлофора.
Визначимо мінімальне значення tо. Нехай задано величини tс, kij, ![]() .
.
Введемо наступні позначення:
tср – середній час проїзду між перехрестями;
tр – час розгону автомобіля;
tг – час гальмування автомобіля;
tч – тривалість горіння червоного сигналу світлофора;
tз – тривалість горіння зеленого сигналу світлофора;
Dt – проміжок між двома автомобілями, що їдуть.
Тоді час синхронізації та загальний час очікування в залежності від одного з випадків визначаються наступними умовами:
1. Якщо всі автомобілі залишаються на червоне світло та чекають однаковий час, то шукані параметри знаходяться з виразів:
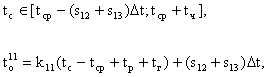 (4)
(4)
де s12 – кількість автомобілів потоку P12, що залишились перед червоним світлом.
2. Якщо частина транспортних засобів проїжджає на зелений сигнал, а решта очікує при червоному світлі, то:
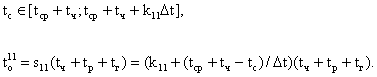 (5)
(5)
3. Якщо усі автомобілі проїжджають на зелений сигнал, то відповідні значення параметрів часу дорівнюють:
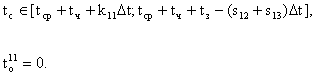 (6)
(6)
Висновки. Таким чином, в даній роботі запропоновано модель управління режимами роботи світлофорної сигналізації на системі перехресть, що побудована на основі апарату нечіткої логіки. Модель дозволяє вибирати оптимальні варіанти регулювання сигналів світлофора на перехресті таким чином, щоб транспортні засоби перебували у системі найменший час, що в свою чергу сприяє рішенню таких важливих проблем транспортних потоків, як дорожні затримки та транспортні затори.
A case the modes of operations of the traffic-light signaling of the system of crossings frame is offered.
1. Лобанов Е.М., Сильянов В.В. и др. Пропускная способность автомобильных дорог. – М.: Транспорт, 1970. – 150 с.
2. Печерский М.П., Хорович Б.Г. Автоматизированные системы управления дорожным движением в городах. – М.: Транспорт, 1979. – 176 с.
3. Барышев М.Л., Драчевский В.И., Капитанов В.Т. Исследования эффективности автоматизированных систем управления дорожным движением: Методические рекомендации. – М.: ВНИЦБД МВД СССР, 1990. – 56 с.
4. Брайловский Н.О., Грановский Б.Н. Управление движением транспортных средств. – М.: Транспорт, 1976. – 110 с.
5. Гаврилов А.А. Моделирование дорожного движения. – М.: Транспорт, 1980. – 189 с.
6. Клинковштейн Г.И. Организация дорожного движения. Учебник для автомобильно-дорожных вузов и факультетов. – М.: Транспорт, 2001. – 192 с.
7. Рябиков Н.А., Байбулатов X.А., Байбулатова Н.X. О факторах, влияющих на формирование автотранспортных потоков. Транспорт: наука, техника, управление. – М.: ВИНИТИ, 2001.
8. Петров В.В., Шрайбер Л.3. Анализ распадения группы автомобилей на перегоне. - В кн.: Технико-экономическое обоснование параметров дорог. Сб.научных трудов ОмПИ, Омск, 1986, с.44-47.
9. Романов А. Г. Закономерности дорожного движения в городах. – М.: ВНИИБД МВД СССР, 1980. – 82 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.