УДК 681.5; 004.94
ПОРІВНЯЛЬНИЙ АНАЛІЗ КЕРУВАННЯ РЕГУЛЯТОРОМ НА ОСНОВІ ЛОКАЛЬНОЇ МОДЕЛІ КЕРОВАНОГО ПРОЦЕСУ ТА П-РЕГУЛЯТОРОМ
Вступ. Одним із найбільш поширених методів регулювання замкнених динамічних систем зі зворотнім зв’язком є використання PID-регуляторів (Proportional-Integral-Derivative) [1], що дозволяють реалізувати керування для багатьох практичних задач, особливо в тих випадках, коли динаміка процесу є стійкою та технічні вимоги до робочих характеристик є обмеженими.
В більшості випадків синтез керування вимагає наявності математичної моделі керованого процесу. На практиці за умови малої апріорної інформації про динаміку об'єкта керування та зовнішні впливи синтез моделі керованого процесу в реальному часі класичними методами на основі дуального керування та статистичної теорії прийняття рішень [2, 3] неможливий через складність обчислюваного порядку [4].
В [5, 6] показано, що модель керованого процесу для таких систем може бути створена на основі сигналу керування, вплив якого на об’єкт керування в поточний момент часу є еквівалентним дії зовнішніх невідомих збурень. Запропонований в [5, 6] метод активно-резонансного (АР) керування дозволяє синтезувати локальну модель керованого процесу (ЛМКП) в реальному часі в умовах малої апріорної інформації про об'єкт керування та зовнішні збурення.
Отже, виникає задача порівняння можливостей стабілізації об'єкта керування регулятором на основі алгоритму синтезу ЛМКП (АР-регулятор) і регулятором на основі широковідомого закону керування, оскільки принципи побудови і функціонування цих регуляторів різні.
Пропорційний (П) регулятор реалізує найбільш простий і поширений закон керування, при якому керуючий вплив лінійно залежить від відхилення вихідної керованої реакції системи.
Метою роботи є розробка методики і проведення порівняльного аналізу стабілізації об'єкта керування АР-регулятором та П-регулятором.
Постановка задачі. Розробку методології порівняльного аналізу властивостей регулятора на основі ЛМКП і П-регулятора виконаємо на прикладі системи керування зі зворотним зв'язком, що містить об'єкт керування, на який діє зовнішнє збурення, та регулятор, що формує сигнал керування.
Розглянемо систему керування, що задана наступним чином [7, 8]:
|
|
(1) |
|
|
(2) |
|
|
(3) |
де t, [с] – час моделювання; ![]() , [с], – інтервал дискретизації; i – порядковий номер часового відліку; y(t), [Н] – вихідна реакція керованого об'єкта; u(t), [Н] – керуючий сигнал регулятора; f(t) – сигнал зовнішнього збурення з параметрами: A, [Н] – амплітуда; ω, [с-1] – кутова частота; φ, [рад] – фазовий зсув; Aob, Bob – коефіцієнти підсилення об'єктом керування сигналу зовнішнього збурення та керуючого сигналу, відповідно.
, [с], – інтервал дискретизації; i – порядковий номер часового відліку; y(t), [Н] – вихідна реакція керованого об'єкта; u(t), [Н] – керуючий сигнал регулятора; f(t) – сигнал зовнішнього збурення з параметрами: A, [Н] – амплітуда; ω, [с-1] – кутова частота; φ, [рад] – фазовий зсув; Aob, Bob – коефіцієнти підсилення об'єктом керування сигналу зовнішнього збурення та керуючого сигналу, відповідно.
Один із можливих алгоритмів створення ЛМКП на основі пробних керувальних впливів і лінійного прогнозу поведінки керованого об’єкта й активно-резонансний алгоритм стабілізації з її використанням докладно описані в [5, 6].
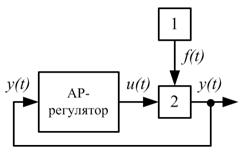
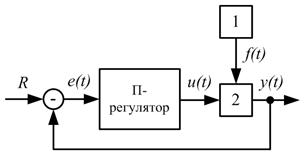
На рис. 1 наведено структурні схеми системи керування з АР- та П-регулятором:
|
|
|
|
а) |
б) |
Рис. 1 Структура системи:
а) АР-регулятор, б) П-регулятор;
1 – блок зовнішнього збурення, 2 – об'єкт керування,
e(t) – похибка керування, R – задавальне значення
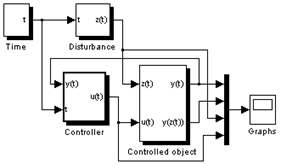
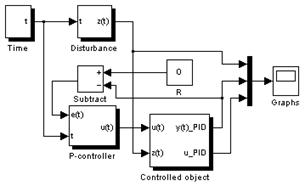
Розробка імітаційних моделей. Імітаційну модель процесу керування системою з П-регулятором (рис. 2 б) було створено на основі розробленої в [7, 8] імітаційної моделі системи керування з регулятором на основі ЛМКП (рис. 2 а) в пакеті MATLAB / Simulink.
|
|
|
|
а) |
б) |
|
|
|
Рис. 2 Схема імітаційної моделі системи керування в пакеті MATLAB / Simulink з:
а) регулятором на основі ЛМКП, б) П-регулятором
Розроблені імітаційні моделі мають наступні однакові блоки (підсистеми): Time – блок генерування часу, Disturbance – блок генерування зовнішніх збурень, Controlled Object – блок моделювання динаміки об'єкта керування. Відмінними є наступні блоки: Controller – блок регулятора на основі ЛМКП, та P-controller – блок П-регулятора.
Методика порівняльного аналізу стабілізації об'єкта керування. Для проведення аналізу необхідно визначити адекватні характеристики регуляторів, що забезпечують еквівалентність їх функціонування, та отримати порівнювані залежності.
Для спрощення сприйняття результатів порівняння введемо наступні умовні позначення. Нехай:
uAR(t), uP(t), [H] – сигнал керування регулятора на основі ЛМКП та П-регулятора, відповідно;
N – кількість часових відліків синтезу ЛМКП АР-регулятором,
Nopt – оптимальна кількість часових відліків синтезу ЛМКП АР-регулятором, що визначається як 1/16 півперіоду зовнішнього збурення згідно доведеній в [9] гіпотезі про наявність оптимальної кількості часових відліків синтезу еквіваленту сигналу зовнішнього збурення в активно-резонансному алгоритмі керування;
Kp – пропорційний коефіцієнт П-регулятора;
Ymax_AR, Ymax_P, [H] – максимальне відхилення вихідної реакції y(t) об’єкта при керуванні регулятором на основі ЛМКП та П-регулятором, відповідно;
YAR, [H] – відхилення вихідної реакції y(t) об’єкта при керуванні АР-регулятором на часовому інтервалі синтезу ЛМКП;
Dm_AR_A = Ymax_AR /A, DP_A = Ymax_P / A – відношення максимального відхилення вихідної реакції y(t) об’єкта при керуванні АР-регулятором та П-регулятором до амплітуди зовнішнього збурення, відповідно, (безрозмірна величина);
DAR_A = YAR /A – відношення відхилення керованої реакції y(t) об’єкта керування при керуванні АР-регулятором на часовому інтервалі синтезу ЛМКП до амплітуди зовнішнього збурення, (безрозмірна величина);
Dm_AR_ω = Ymax_AR /ω, DP_ω = Ymax_P / ω – відношення максимального відхилення вихідної реакції y(t) об’єкта при керуванні АР-регулятором та П-регулятором до кутової частоти зовнішнього збурення, відповідно, (безрозмірна величина);
DAR_ω = YAR /ω – відношення відхилення керованої реакції y(t) об’єкта керування при керуванні АР-регулятором на часовому інтервалі синтезу ЛМКП до кутової частоти зовнішнього збурення, (безрозмірна величина);
![]() – порядковий номер.
– порядковий номер.
Порівняльний аналіз стабілізації об'єкта керування П-регулятором і регулятором на основі ЛМКП будемо виконувати за наступним алгоритмом:
1) визначення параметрів імітаційної моделі з АР- та П-регулятором, а саме:
– коефіцієнтів підсилення об’єкта керування;
– параметрів зовнішнього збурення f(t);
– кількості часових відліків N синтезу ЛМКП АР-регулятором;
– задавального значення для П-регулятора;
– часу функціонування імітаційної моделі.
2) забезпечення адекватного моделювання, при якому керуючі сигнали регуляторів мають бути еквівалентними на часовому інтервалі синтезу ЛМКП для встановлених параметрів, що здійснюється обчисленням методом найменших квадратів коефіцієнта Kp, при якому uAR(t) = uP(t) на часовому інтервалі синтезу АР-регулятором ЛМКП;
3) отримання результатів моделювання:
а) запуск імітаційних моделей системи керування з відповідними регуляторами;
б) фіксування значень Ymax_AR, YAR та Ymax_P вихідної реакції y(t) об’єкта керування для встановлених параметрів.
4) порівняння наступних характеристик:
– залежність Ymax_AR, YAR та Ymax_P від амплітуди зовнішнього збурення;
– залежність Ymax_AR, YAR та Ymax_P від кутової частоти зовнішнього збурення;
– відношення Ymax_AR, YAR та Ymax_P до амплітуди і частоти збурення f(t);
– фазовий зсув між вихідною реакцією y(t) об'єкта керування та сигналом зовнішнього збурення f(t).
Порівняльний аналіз стабілізації. В табл. 1 наведено параметри зовнішнього збурення f(t), для яких аналізувались результати імітаційного моделювання.
Таблиця 1
Параметри f(t)
|
А |
ω, с-1 |
φ |
|
1, 2, ..., 10 |
|
0 |
|
|
В табл. 2 наведено значення коефіцієнту Kp при фіксованому та оптимальному значенні N для вказаних в табл. 1 параметрів зовнішнього збурення:
Таблиця 2
Коефіцієнт Kp для різних значень N та ω
|
ω1, с-1 |
Kp при N=10 |
Nopt |
Kp |
|
ω2, с-1 |
Kp при N=10 |
Nopt |
Kp |
|
π/5 |
0,163393 |
30 |
0,164697 |
π |
0,163534 |
6 |
0,171218 |
|
|
2∙π/5 |
0,16341 |
16 |
0,163476 |
π/2 |
0,163424 |
13 |
0,162381 |
|
|
3∙π/5 |
0,16344 |
10 |
0,16344 |
π/3 |
0,163403 |
19 |
0,163432 |
|
|
4∙π/5 |
0,163481 |
8 |
0,164951 |
π/4 |
0,163396 |
25 |
0,164148 |
|
|
5∙π/5 |
0,163534 |
6 |
0,171218 |
π/5 |
0,163393 |
30 |
0,164697 |
|
|
6∙π/5 |
0,163599 |
5 |
0,174869 |
π/6 |
0,163391 |
38 |
0,165082 |
|
|
7∙π/5 |
0,163676 |
4 |
0,200188 |
π/7 |
0,16339 |
44 |
0,165287 |
|
|
8∙π/5 |
0,161638 |
4 |
0,200245 |
π/8 |
0,163389 |
50 |
0,165446 |
|
|
9∙π/5 |
0,163866 |
4 |
0,200311 |
π/9 |
0,163389 |
56 |
0,165573 |
|
|
10∙π/5 |
0,16398 |
4 |
0,200383 |
π/10 |
0,163388 |
63 |
0,16566 |
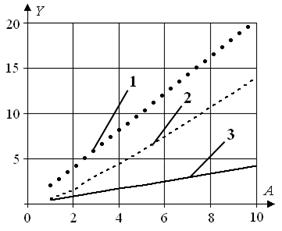
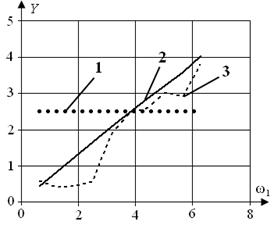
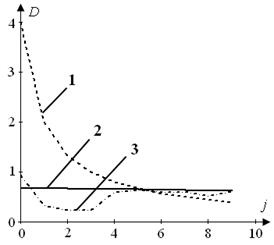
На рис. 6 та рис. 7 наведено приклади залежності максимального відхилення вихідної реакції y(t) об'єкта керування від амплітуди A зовнішнього збурення та його відношення до цих значень амплітуди при ω = π/5, φ = 0, відповідно.
|
|
|
|
а) |
б) |
Рис. 6 Залежність максимального відхилення вихідної реакції y(t)
від амплітуди A зовнішнього збурення при:
а) N, б) Nopt; 1 – Ymax_P, 2 – YAR, 3 – Ymax_AR
|
|
|
|
а) |
б) |
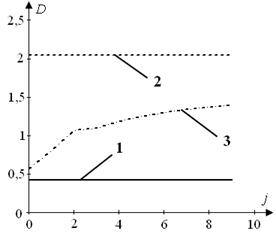
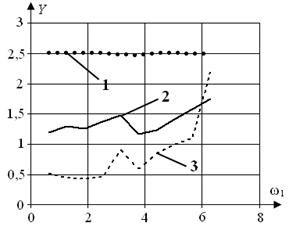
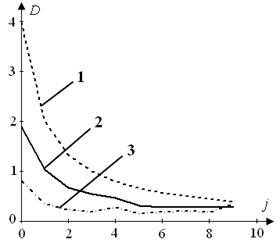
Рис. 7 Відношення максимального відхилення реакції y(t)
до амплітуди А при:
а) N, б) Nopt; 1 – DP_A, 2 – DAR_A , 3 – Dm_AR_A
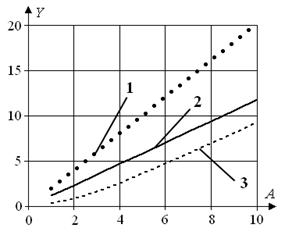
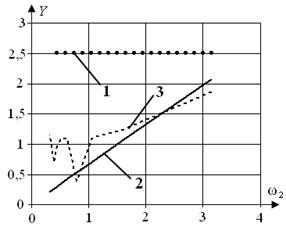
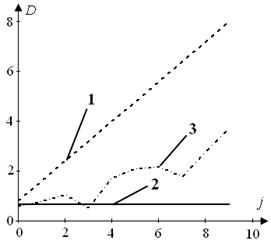
На рис. 8 наведено приклади залежності максимального відхилення вихідної реакції y(t) об'єкта керування від значень кутової частоти при A = 1, φ = 0:
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
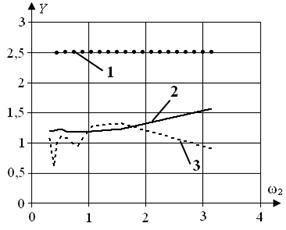
Рис. 8 Залежність максимального відхилення вихідної реакції y(t) від кутової частоти:
а) ω1 при N, б) ω1 при Nopt, в) ω2 при N, г) ω2 при Nopt; 1 – Ymax_P, 2 – YAR , 3 – Ymax_A
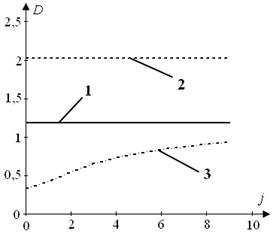
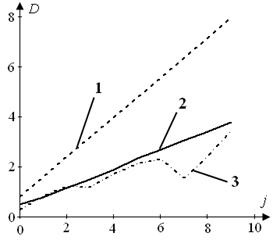
На рис. 9 наведено приклади відношення максимального відхилення вихідної реакції y(t) об'єкта до значень кутової частоти ω при A = 1, φ = 0.
Фазовий зсув між вихідною реакцією y(t) об'єкта керування та сигналом зовнішнього збурення f(t) не залежить від його кутової частоти ω та є нульовим як при фіксованому N, так і при оптимальному Nopt.
Висновки. Таким чином, розроблена методика дозволяє проводити порівняльний аналіз стабілізації об'єкта керування регулятором на основі ЛМКП і пропорційним регулятором. З проведеного дослідження можна зробити наступні висновки:
1) максимальне відхилення вихідної реакції y(t) об'єкта керування при стабілізації АР-регулятором залежить від амплітуди A зовнішнього збурення f(t) лінійно як при фіксованому N = 10, так і при оптимальному Nopt значеннях кількості часових відліків синтезу ЛМКП, аналогічно П-регулятору;
2) на часовому інтервалі півперіоду сигналу зовнішнього збурення як при фіксованому N = 10, так і при оптимальному Nopt значеннях кількості часових відліків синтезу ЛМКП максимальне відхилення вихідної реакції y(t) об'єкта керування при стабілізації АР-регулятором залежить від значень кутової частоти ω зовнішнього збурення нелінійно та може бути апроксимоване поліномом 6-го порядку з коефіцієнтом детермінації близьким до 1, на відміну від стабілізації П-регулятором, при дії якого максимальне відхилення вихідної реакції y(t) об'єкта керування не залежить від значень кутової частоти ω зовнішнього збурення f(t), і є сталим;
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
Рис. 9 Відношення максимального відхилення вихідної реакції y(t) до кутової частоти: а) ω1 при N, б) ω1 при Nopt, в) ω2 при N, г) ω2 при Nopt; 1 – DP_ω, 2 – DAR_ω , 3 – Dm_AR_ω
2) на часовому інтервалі півперіоду сигналу зовнішнього збурення як при фіксованому N = 10, так і при оптимальному Nopt максимальне відхилення вихідної реакції y(t) об'єкта керування при стабілізації АР-регулятором залежить від значень кутової частоти ω зовнішнього збурення нелінійно та може бути апроксимоване поліномом 6-го порядку з коефіцієнтом детермінації близьким до 1, на відміну від стабілізації П-регулятором, при дії якого максимальне відхилення вихідної реакції y(t) об'єкта керування не залежить від значень кутової частоти ω зовнішнього збурення f(t), і є сталим;
3) на часовому інтервалі синтезу ЛМКП максимальне відхилення вихідної реакції y(t) об'єкта керування при фіксованому N залежить від кутової частоти ω зовнішнього збурення лінійно, а при оптимальному Nopt – нелінійно та може бути апроксимоване поліномом 6-го порядку з коефіцієнтом детермінації близьким до 1, на відміну від стабілізації П-регулятором, при дії якого максимальне відхилення вихідної реакції y(t) об'єкта не залежить від значень кутової частоти ω зовнішнього збурення f(t), і є сталим;
4) при стабілізації АР-регулятором максимальне відхилення вихідної реакції y(t) об'єкту керування є меншим порівняно зі стабілізацією П-регулятором, що є перевагою регулятора на основі ЛМКП.
Розроблена в даній роботі методика проведення порівняльного аналізу процесу стабілізації об'єкта керування регулятором на основі ЛМКП і П-регулятором може бути використана для побудови і порівняння АЧХ, ЛАЧХ, ФЧХ, АФЧХ вихідного сигналу системи керування з регулятором на основі ЛМКП і пропорційним регулятором.
ЛІТЕРАТУРА
1. K. Astrom, T. Huggland. PID Controllers: Theory, Design and Tuning. 2nd edition. – North Carolina, USA: Instrument Society of America, Research Triangle Park, 1995. – 343 p.
2. Справочник по теории автоматического управления. /Под. ред. А.А. Красовского. – М.: Наука., 1987. – 712 с.
3. Фельдбаум А.А. Основы теории оптимальных автоматических систем. Изд.2, испр. и доп.– М.: «Наука», 1966. – 624 с.
4. Кунцевич В.М. Управление в условиях неопределенности: гарантированные результаты в задачах управления и идентификации. – Киев: Наук. Думка, 2006. – 264 с.
5. Гученко М.І. Активно-резонансний алгоритм стабілізації. – Нові технології. Науковий вісник Інституту економіки та нових технологій ім. Ю.І. Кравченка, № 1(2), 2003. – c. 57-61.
6. Гученко М.І. Активно-резонансний принцип керування // Збірник тез доповідей 16 Міжнародної конференції з автоматичного управління "Автоматика – 2009". Чернівці, 22 – 25 вересня, 2009, с. 59-61.
7. Славко Е.Г., Гученко Н.И. Реализация алгоритма активного резонанса в среде Simulink для задачи стабилизации динамической систем // Тезисы докладов Двенадцатой Международной научно-технической конференции “Моделирование, идентификация, синтез систем управления”, Москва-Донецк. – 16-23 сентября 2009. – с. 70-71.
8. Славко О.Г., Гученко М.І. Побудова імітаційної моделі активно-резонансного регулятора // Збірник тез VII Міжнародної науково-практичної конференції "Математичне та програмне забезпечення інтелектуальних систем" (MPZIS-2009). – м. Дніпропетровськ, 2009. – с. 254-255.
9. Гученко Н.И., Славко Е.Г., Серик М.Ю., Иванова М.Н. Исследование влияния времени моделирования сигнала возмущения на точность стабилизации управляемой системы. – Вісник Кременчуцького державного політехнічного університету, № 2/2006(37). – Кременчук, 2006. – с. 12-15.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииВойтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.