Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 004.75

ГЕНЕТИЧНІ АЛГОРИТМИ ВИРІШЕННЯ ЗАДАЧ УПРАВЛІННЯ РЕСУРСАМИ І НАВАНТАЖЕННЯМ ЦЕНТРІВ ОБРОБЛЕННЯ ДАНИХ

Теленик С.Ф., Ролік О.І., Букасов М.М., Андросов С.А.

Вступ. Глобальна інформатизація, викликана стрімким розвитком інформаційних технологій (ІТ), обумовила зростання вимог до кількісних і якісних параметрів інформаційного обслуговування бізнесу [1]. Реакцією на ці процеси стало поширення інформаційно-телекомунікаційних систем (ІТС), призначених для підтримки процесів прийняття управлінських рішень міністерств, відомств і великих корпорацій. Створення високопродуктивної, надійної ІТ-інфраструктури ІТС реалізується на основі центрів оброблення даних (ЦОД) — комплексних організаційно-технічних рішень. Основними завданнями ЦОД є консолідоване зберігання і оброблення даних користувачів, надання їм прикладних сервісів, підтримка функціонування застосувань.

У галузі ІТ накопичений певний досвід створення і експлуатації ЦОД. Він підтвердив, що експлуатація ЦОД можлива лише за наявності організаційної структури, оснащеної сучасним інструментарієм та комплексом методик збору, аналізу інформації, прийняття рішень та управління їх відпрацюванням. Їх створення вимагає глибокого розуміння функціонування ІТ-інфраструктури, чіткої постановки проблем дослідження, розроблення математичних моделей і відповідних методів вирішення задач та, насамкінець, реалізації згаданих інструментарію та методик у структурі системи управління ІТ-інфраструктурою (СУІ).

Серед проблем, які ще потребують розв’язання, залишається важлива проблема управління продуктивністю ІТ-інфраструктури і насамперед базова її складова — розподіл і управління навантаженням і ресурсами ЦОД. Також вимагають ефективного розв’язання проблеми управління рівнем обслуговування користувачів мереж, впливу неполадок у мережі на рівень обслуговування користувачів, виявлення нелигитимного використання ресурсів операторів зв’язку та інші проблеми [2—4].

У статті автори на основі узагальнення накопиченого досвіду розв’язання проблеми розподілу і управління навантаженням і ресурсами центрів оброблення даних пропонують модифікації раніше розроблених моделей, які більш вдало враховують реалії цієї цікавої галузі досліджень. З метою розроблення універсального алгоритму для цього класу задач авторами пропонується варіант керованого генетичного алгоритму. Керованість означає вплив на вибір чергових операторів формування популяції у залежності від деяких важливих її параметрів. Шляхом налаштування зазначених параметрів керований генетичний алгоритм (ГА) можна досить швидко «навчити» розв’язувати різноманітні проблеми зазначеного класу, особливістю яких є складний характер взаємодії критеріїв і обмежень, що раніше часто призводило до передчасного виродження популяції.

1 Розподіл і управління навантаженням і ресурсами ЦОД: досвід практичного впровадження і експериментальних досліджень. Комплекс моделей розподілу і управління навантаженням і ресурсами ЦОД для різних технологій хостингу запропонований авторами у циклі праць [5—10], зокрема для випадків:

— віртуального хостингу [5, 6]: дискретний і неперервний варіанти моделі;

— виділених серверів [7];

— серверної віртуалізації [8].

У кожній із зазначених робіт проблема розподілу і управління навантаженням і ресурсами ЦОД розв’язувалась шляхом реалізації послідовно (за необхідності, ітеративно) виконуваних етапів планування, управління і диспетчеризації ресурсів і навантаження.

Задачі планування та управління розподілом ресурсів і навантаженням зводяться до оптимізаційних проблем вигляду:

                                                              ,                                                                        (1)

де f(x): Ω → R — функція, яка визначає ефективність рішення х, критерій оптимальності, оснований на конкретній постановці задачі управління, Ω — область допустимих рішень. Без втрати узагальненості результатів можна вважати, що f(x) ≥ 0, а Ω — дискретний або неперервний простір (в залежності від обраного варіанту математичної моделі).

Функція f(x) та область Ω залежать від технологій хостингу, побудови прикладного програмного забезпечення, кластеризації і віртуалізації, а також прийнятих критеріїв ефективності і ресурсних, технологічних та інших актуальних обмежень.

Для задачі управління при віртуальному хостингу зазначені вище математичні моделі були формалізовані наступним чином [5, 6]:

N={N₁,…,N_n} — множина серверів, кількість яких дорівнює n;

А={А₁,…,А_m} — множина застосувань, кількість яких дорівнює m;

З опису системи, яка моделюється, легко зрозуміти, що потребу в обчислювальних потужностях можуть забезпечити декілька серверів своєю сумарною процесорною місткістю (у випадку розподілених обчислень). Тоді на кожному з обраних сервері розміщується екземпляр застосування, якщо потреби в оперативній пам’яті, пам’яті жорстких дисків та пропускній здатності каналів повністю задовольняються ресурсами кожного окремого серверу.

Для позначення результату (шуканого оптимального розміщення) у математичній моделі вводиться матриця X=||x_ji||, де

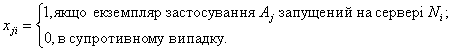
для дискретного варіанту моделі, і

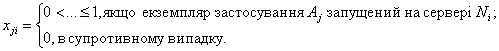
для неперервного, при якому значення x_ji відповідає частці процесорного часу, виділеній на i-му сервері для j-го застосування.

Для неперервного варіанту реалізації моделі вводиться додатковий параметр, який характеризує факт наявності екземпляру певного застосування на сервері:

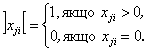                                                                                                                   (2)

Оптимальне розміщення X=||x_ji|| повинне враховувати такі обмеження:

— сумарні незалежні від навантаження вимоги визначених для розміщення на сервері екземплярів застосувань не перевищують відповідні параметри сервера;

— сумарні залежні від навантаження вимоги визначених для розміщення на сервері екземплярів застосувань не перевищують відповідні параметри сервера;

— залежні від навантаження вимоги застосувань повинні бути забезпечені сумарними можливостями ресурсів тих серверів, на яких розміщуються екземпляри відповідних застосувань;

— обмеження, пов’язані з можливістю розгортання застосування А_j на сервері N_і.

У розглянутому циклі робіт [5—10] для розв’язку були обрані наступні задачі з оптимізації розподілу ресурсів і навантажень:

1) Задача мінімізації витрат на підтримку клієнтських запитів. Тобто вибирається така мінімальна за витратами на їх підтримку підмножина серверів, які зможуть підтримати необхідну для задоволення вимог існуючих користувачів множину екземплярів застосувань.

У контексті задачі вводиться додаткова змінна y_i, що характеризує зайнятість і-го сервера.

Формалізація критерію має наступний вигляд:

                                                             ,                                                                       (3)

де s_i — вартість підтримки серверу N_і.

Змінна зайнятості сервера приймає наступні значення:

— для дискретного варіанту: у_і = х_1і Ú х_2і Ú…Ú х_mі, і=1,…,n.

— для неперервного варіанту: у_і = ]х_1і[Ú ]х_2і[Ú…Ú ]х_mі[, і=1,…,n.

2) Задача рівномірного завантаження серверів з метою уникнути відмов у обслуговуванні користувачів у разі різкого збільшення навантаження.

Формалізація критерію для дискретного варіанту розподілу:

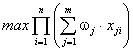                                                      ,                                                               (4)

де w_j — вимоги застосування А_j до процесорної місткості серверів, а для неперервного:

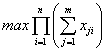                                                         .                                                                   (5)

3) Задача мінімізації сумарних витрат на підтримку клієнтських запитів і реалізацію переходу до нового оптимального плану розміщення застосувань.

Формалізація критерію для дискретного варіанту розподілу:

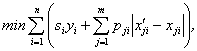                                                                                                       (6)

а для неперервного:

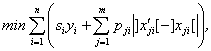                                                                                                   (7)

де значення параметру p_ji відповідає вартості розгортання певного застосування на певному сервері, а  характеризує початковий план розташування застосувань на серверах.

Для вирішення сформульованих задач управління розподілом ресурсів і навантаженням у роботах були використані:

— базовий варіант ГА;

— евристичні алгоритми з урахуванням специфіки критеріїв і обмежень.

Результати виконаних експериментів продемонстрували працездатність обраних методів.

Нижче наведені характеристики залежності одержаного оптимального значення критерію (цільової функції (ЦФ)) від розмірності задачі (кількості серверів та застосувань, що плануються до розміщення на серверах). Аналізуючи характеристики, можна порівняти оптимальність результатів евристичних та генетичних методів пошуку рішень. З огляду на те, що ГА для різних початкових параметрів популяції може давати різні рішення, на графіках присутні дві величини, що характеризують ГА: кращий варіант розв’язку, отриманий під час експериментів, та середнє значення оптимальності отриманого розв’язку.

Отримані характеристики:

1) Характеристики до задачі мінімізації витрат на підтримку клієнтських запитів (3) (за ординату береться відношення величини ЦФ до загальної вартості усіх серверів):

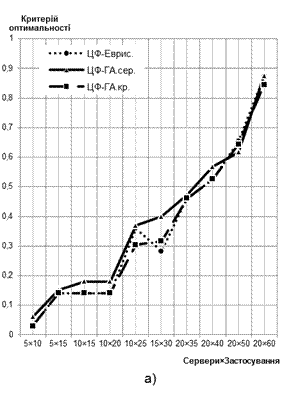
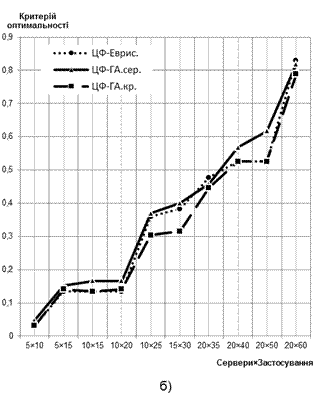
Рис. 1 Залежність значення ЦФ від розмірності вирішуваної задачі:
а) дискретний варіант формулювання задачі; б) неперервний варіант формулювання задачі

На основі отриманих характеристик можна зробити ряд висновків, зокрема:

— як генетичний, так і евристичний алгоритм пошуку оптимального рішення показали себе придатними до застосування у задачах подібного типу;

— середнє значення результату, одержаного за допомогою ГА, дещо гірше, ніж значення евристичного. Це можна пояснити наявністю багатьох випадкових процесів у основі виконання ГА, що зумовлюють певну непередбачуваність кінцевих результатів (випадковість складу початкової популяції, випадковість мутації та точки кросоверу);

— хоча середнє значення оптимуму ГА і менше, ніж евристичного, та на графіку чітко видно, що кращий результат ГА не поступається, а інколи навіть перевершує результати евристичного алгоритму (задача мінімізації — кращий результат знаходиться нижче по осі ординат). Це можна пояснити тим, що структура та сутність ГА дозволяє йому уникати «локальних оптимумів», та досягати їх «глобальних» значень;

— варто зауважити, що рівномірність результату неперервного варіанту значно більша, ніж у дискретного. Це можна пояснити тим фактом, що обчислювальні потужності ЦОД при неперервному варіанті використовуються значно кращим чином, ніж при дискретному.

2) Задача рівномірного завантаження фізичних серверів (4, 5).

За ординату береться відношення величини ЦФ розв’язку до теоретично розрахованого оптимуму критерію, абсцисою є розмірність задачі — Сервери×Застосування. Характеристики будуються для обох варіантів математичної моделі:

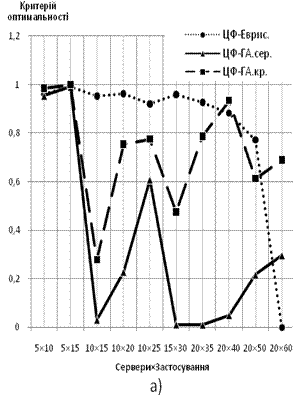
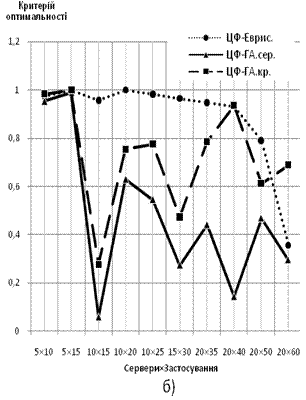
Рис. 2 Залежність значення ЦФ від розмірності вирішуваної задачі:
а) дискретний варіант формулювання задачі; б) неперервний варіант формулювання задачі

Як видно із результатів, отриманих у ході експерименту, метод, оснований на використанні ГА, досяг значно гірших за оптимальністю розв’язків, ніж евристичний підхід.

Одержані результати можливо пояснити тим, що для кожного специфічного критерію оптимальності, що використовується для знаходження кращого розв’язку, необхідно певним чином модифікувати структуру ГА в плані генерації початкових випадкових даних стартової популяції, операцій кросоверу і мутації задля покращення збіжності до оптимуму процесів пошуку ГА.

Причина більшості збоїв ГА при тестуванні реалізації даної задачі була викликана специфікою початкових даних, на основі яких будувалась робота ГА.

В деяких випадках, як і у попередній задачі, ГА досягав значень показника оптимальності кращих, ніж евристичний. Причина у наявності «локальних» та «глобальних» оптимумів цільової функції.

3) Задача мінімізації сумарних витрат на підтримку клієнтських запитів і реалізацію переходу до нового оптимального плану розміщення застосувань (6, 7).

За ординату береться відношення величини ЦФ (вартості підтримки з урахуванням переходу) до сумарної вартості підтримки усіх серверів парку, абсцисою є розмірність задачі — Сервери×Застосування. Характеристики будуються для обох варіантів математичної моделі:

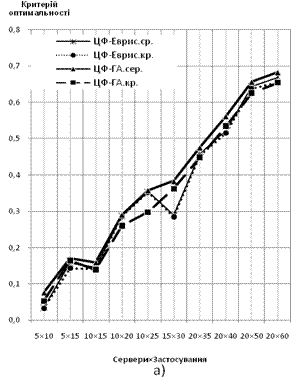
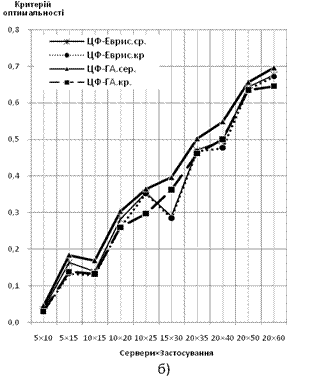
Рис. 3 Залежність значення ЦФ від розмірності вирішуваної задачі:
а) дискретний варіант формулювання задачі;  б) неперервний варіант формулювання задачі

У двох останніх експериментах ГА продемонстрував прийнятну оптимальність у порівнянні з евристичним алгоритмом. Характеристики подібні до характеристик першої із розглянутих задач. Подібність результатів можна пояснити близькістю формулювання критеріїв оптимальності, та більш придатною для даного типа задачі початковою популяцією хромосомних наборів.

Наведені вище результати дозволяють зробити такі висновки:

— як генетичний, так і евристичний алгоритм пошуку оптимального рішення показали себе придатними до застосування у задачах подібного типу;

— експерименти показали, що евристичні алгоритми дозволяють переважно одержувати розв’язки швидше, але з меншим наближенням до оптимуму, тобто оптимальність розв’язків ГА, для деяких задач, перевищує їх евристичні відповідники;

— середнє значення оптимальності розв’язків ГА значно менше, ніж оптимальність кращого з отриманих розв’язків. Це можна пояснити наявністю випадкових процесів, на базі яких будується реалізація ГА: випадковість стартової популяції алгоритму, моменту і позиції мутації та кросоверу;

— для певного класу задач (певного критерію оптимальності) ГА показав кращі результати, ніж для інших. Це вказує на необхідність певного налаштування конкретної реалізації ГА під потреби конкретної задачі, задля забезпечення необхідного характеру збіжності процесів пошуку оптимуму. Окрім налаштувань ГА під конкретну задачу є можливість змінити формулювання критерію оптимальності, без втрати логіки оптимізації.

На основі проведених досліджень можна сказати, що, по-перше, запропоновані моделі працюють, але в окремих випадках вимагають деяких уточнень. По-друге, використання класичного генетичного алгоритму не завжди дає потрібну точність результату, а адаптація алгоритму під кожну окрему задачу вимагає достатньо великих витрат часу.

2 Постановка проблеми поглиблення досліджень. З урахуванням зазначеного вище, метою цього дослідження є уточнення окремих моделей управління ресурсами і навантаженням ЦОД, а також розроблення універсального ГА, який можна було б просто налаштовувати на специфіку різних задач розподілу і управління ресурсами і навантаженням.

3 Модифікація і розвиток існуючих моделей. В ході аналізу методів пошуку оптимального розподілу ресурсів і навантаження, а також проведення експериментів було вирішено внести точність у формулювання критерію оптимальності задачі мінімізації сумарних витрат на підтримку клієнтських запитів і реалізацію переходу до нового оптимального плану розміщення застосувань. У формулах (6) та (7) модулі різниць та  будуть дорівнювати 1 тільки у випадку, коли на певному сервері не було застосування у попередньому плані і з’явилось у новому ( та ). Випадок, коли застосування зникає із серверу у зв’язку з переходом до нового плану, не несе витрат на перенесення програмного забезпечення.

4 Керований генетичний алгоритм. Оскільки проблеми проектування, аналізу і управління ІТС становлять окремий клас проблем великої вимірності, то для ГА при вирішенні цих проблем важливою умовою є ефективне управління збіжністю. Тобто необхідно мати такий механізм у ГА, який, виходячи із вимірності задачі і заданої точності рішень, міг би знайти потрібний компроміс між кількістю кроків алгоритму і точністю рішень.

Виникає необхідність розробити керований ГА для розв’язання цієї проблеми і обґрунтувати його збіжність. Керований ГА повинен враховувати особливості проблеми, характеристики попередньої популяції і послідовності найкращих рішень з метою визначення такої послідовності операторів кросинговеру, мутації та вибору, яка забезпечує найшвидшу збіжність.

Розглянемо універсальну схему застосування ГА з контрольованою збіжністю до класу задач проектування, аналізу і оптимізації ІТС. На рисунку 4 наведена блок-схема керованого ГА.

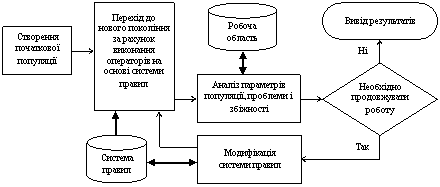
Рис. 4 Блок-схема керованого генетичного алгоритму

Основна відмінність запропонованого керованого ГА від базового ГА, розглянутого раніше, полягає у механізмі отримання нової популяції особин на базі представників минулої епохи.

У базовому варіанті ГА отримання популяції нової епохи відбувалось шляхом послідовного виконання операторів кросоверу (С), мутації (М) (з певною вірогідністю, над нащадком, одержаним з кросоверу) та селекції (S) (відбір кращих з одержаних результатів). Певного роду селекція відбувалась також перед кросовером при відборі за певним принципом особин, що братимуть у кросовері участь. Таким чином, у формуванні популяції кожної наступної епохи брали участь усі три типи операторів ГА.

Подібна організація процесу, хоча і давала збіжність пошуку, але не гарантувала оптимальності розв’язку. Це пов’язано із наявністю проблеми балансу «дослідження» і «використання» [11,12], яка полягає у балансуванні між використанням вже існуючого матеріалу (закріплення оптимальних схем розв’язку за допомогою кросоверу) та дослідженням нових оптимумів, що не входять до вивченого простору (отримання якісно нових схем за допомогою використання мутації). Велика кількість мутацій може привести до руйнування схеми кращого представника поточної популяції, в той час, як використання кросоверу призводить до підвищення швидкості збіжності процесів пошуку до оптимуму (може бути як «локальним», так і «глобальним»).

Із постановки проблеми видно, що при використанні базового варіанту ГА явних механізмів балансування між «дослідженням» і «використанням» немає. Процеси відбуваються без контролю у послідовності, заданій схемою самого алгоритму.

При використанні керованого ГА (рисунок 4) відбувається забезпечення балансування між «дослідженням» і «використанням» шляхом введення системи правил, на базі якої відбувається вибір оператора (кросоверу чи мутації), у результаті використання якого буде отримана популяція наступної епохи. Таких чином, ми присвячуємо кожну окрему епоху процесу пошуку, або «використанню» існуючого матеріалу (закріпленням оптимальних розв’язків), або «дослідженню» нових областей простору розв’язків. Селекція буде відбуватись у кожному з випадків, залишаючи у складі популяції нової епохи лише кращих представників із сукупності представників минулої епохи та одержаних на їх базі нащадків. У випадку, коли кількість отриманих нащадків буде занадто мала, сукупність, з якої робитиметься відбір, поповнюватиметься додатковим вливанням випадково згенерованих представників — для забезпечення різноманіття генетичного матеріалу популяції.

Для того, щоб сформувати систему правил керованого ГА необхідно вибрати параметри процесу, за якими буде оцінюватись характер його збіжності, та потреба у використанні конкретного оператора алгоритму (С або М) для кожної конкретної епохи. Певні підходи до формулювання таких параметрів процесів наводились авторами [12] у їх дослідженнях збіжності ГА.

Введемо наступні параметри:

— Коефіцієнт приросту популяції.

Під час генерації популяції нової епохи за допомогою використання одного з операторів (С або М) одержана кількість нащадків може бути дуже малою у порівнянні із розміром популяції. Цей факт вказує на вироджуваність популяції, пов’язану з недостатнім різноманіттям генетичного матеріалу, і потребує відповідних дій (додаткового «вливання» нового генетичного матеріалу).

                                                                ,                                                                         (8)

де l — кількість отриманих нащадків, n — розмір популяції.

— Тиск відбору.

Під час роботи ГА необхідно мати параметр, який характеризував би ступінь наближення поточної популяції до оптимуму. Відомо, що алгоритм пошуку зупиниться, коли максимальне значення оптимальності співпаде (або достатньо сильно наблизиться) до середнього значення оптимальності всієї популяції.

Введемо тиск відбору, як величину відношення максимального оптимуму популяції поточної епохи до її середньої оптимальності. При цьому приймемо, що критерієм оптимальності є максимізація значення ЦФ. Тоді тиск відбору дорівнює:

                                                            ,                                                                      (9)

де  — ЦФ пошуку, а  — середнє значення ЦФ поточної популяції.

Із визначення параметру можна зробити висновок, що виконується умова . Значення тиску відбору дорівнює 1 у випадку, коли оптимальність усіх представників популяції рівна.

— Швидкість зміни збіжності.

Необхідно мати параметр, який характеризував би тенденції зміни збіжності ГА при переході від епохи до епохи. Введемо поняття швидкості збіжності, як різницю між значеннями тисків відбору популяцій попередньої та поточної епох:

                                                         .                                                                 (10)

Сформулюємо набір правил, за якими буде обиратись операція для одержання популяції наступної епохи:

1) Якщо коефіцієнт приросту популяції менший за критичне значення, то виникає необхідність проводити додаткове «вливання» нового генетичного матеріалу (оператор RI).

Формалізація правила має вигляд:

                                                  IF () THEN RI;                                                          (11)

2) Якщо значення швидкості збіжності стає від’ємним при переході від k-ої до (k+1)-ої епохи — то для формування популяції наступної епохи буде використовуватись оператор кросоверу (С).

За умови того, що при переході від епохи до епохи середня пристосованість популяції не зменшується (при переході від епохи до епохи відбувається селекція лише кращих представників), швидкість збіжності може стати від’ємною тільки за умови, що тиск відбору поточної епохи став більшим за тиск відбору попередньої. Це, в свою чергу, можливо за умови знаходження нового максимального значення оптимальності, тобто знаходження кращого розв’язку задачі. Заради збереження кращого розв’язку необхідно від стратегії «дослідження» перейти до стратегії «використання», а отже до кросоверу.

Формалізація правила має вигляд:

                                                   IF () THEN C;                                                           (12)

3) Якщо значення швидкості збіжності ГА, а також значення тиску відбору популяції поточної епохи не менші, ніж граничні значення (характер збіжності процесів ще не визначений, немає сходження до «локального» оптимуму), то для одержання популяції наступної епохи використовується кросовер.

Формалізація правила має вигляд:

                                 IF (() AND ()) THEN C;                                        (13)

4) Якщо значення швидкості збіжності, або значення тиску відбору популяції поточної епохи менші за граничні, то для отримання популяції наступної епохи використовується мутація.

В цьому випадку пошук оптимального розв’язку сходиться до певного «локального» оптимуму і потрібно перейти від стратегії «використання» до стратегії «дослідження», а отже до мутації.

Формалізація правила має вигляд:

                                  IF (() OR ()) THEN M;                                         (14)

Окрім правил вибору наступного оператору генерації популяції до системи правил слід також занести правила зупинки процесу пошуку:

5) Якщо швидкість збіжності а також тиск відбору популяції протягом двох епох підряд були менші за критичні — процес зупиняється, відповіддю приймається максимальний оптимум популяції поточної епохи. Умова перевірки на популяціях двох останніх епох вводиться для надання шансу для мутації виявити новий кращий результат у недосліджених областях простору розв’язків.

Формалізація правила має вигляд:

                                         IF ((() AND ())

                            AND (() AND ())) THEN EXIT;                                   (15)

6) Якщо максимум оптимальності популяції поточної епохи стає меншим, ніж максимум оптимальності минулої — процес зупиняється, останньою правильною епохою визнається попередня, а кращим результатом пошуку — максимум оптимуму попередньої епохи.

Формалізація правила має вигляд:

                          IF () THEN STEP_BACK; EXIT;                                 (16)

Як видно із одержаних правил (11 — 16), для організації управління процесами у ГА необхідно задатись початковими значеннями параметрів граничних та критичних швидкостей збіжності та тисків відбору (відповідно ,,,), а також значенням  — критичним для коефіцієнту приросту популяції. Налаштуванням цих коефіцієнтів можна регулювати швидкість збіжності пошуку ГА та характер основних процесів, що в ньому відбуваються. Ці процеси проходять на етапі модифікації системи правил (рисунок 4), що дозволяє влаштувати свого роду зворотній зв'язок по оптимальності отриманого результату.

Варто зазначити, що кількість можливих правил управління процесами у ГА не обмежується описаною раніше множиною. Якщо ввести додаткові показники збіжності ГА, то можна збільшити базу правил схеми, зображеної на рисунку 4. При цьому може виникнути ситуація, при якій для певного набору значень параметрів можуть одночасно спрацьовувати кілька конфліктних правил (правил, що різним чином визначають хід одного і того ж процесу). У цьому випадку слід використовувати систему оцінювання внеску кожного з правил у кінцевий результат (встановлення рангів правил системи або їх динамічне оцінювання у ході процесу на основі якісного внеску кожного окремого правила у кінцевий результат) і обирати із можливої множини найбільш пріоритетні.

5 Експериментальне дослідження керованого ГА. Алгоритм, блок-схема якого зображена на рисунку 4, був програмно реалізований. Після цього була проведена низка експериментів для порівняння оптимальності результатів керованого ГА (КГА) із розробленими евристиками.

Результати експериментів:

1) Характеристики до задачі мінімізації витрат на підтримку клієнтських запитів. Оскільки за умовами правил задача має бути задачею максимізації, змінимо критерій задачі. Від мінімізації витрат перейдемо до максимізації економії, в якості величини економії ввівши різницю між вартістю підтримки усіх серверів серверного парку та мінімальними витратами із початкової задачі. Маємо критерій нової задачі:

                                                                                                                         (17)

де S — сумарна вартість підтримки серверів серверного парку.

За ординату береться відношення величини ЦФ до загальної вартості усіх серверів поточної конфігурації, за абсцису — розмірність задачі:

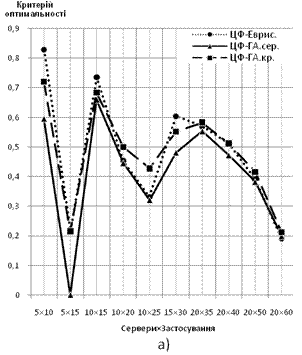
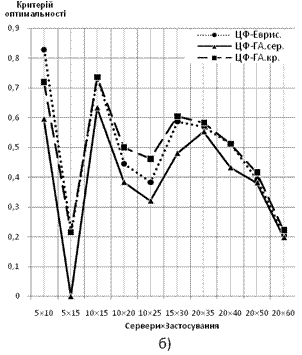
Рис. 5 Залежність значення ЦФ від розмірності вирішуваної задачі: а) дискретний варіант формулювання задачі; б) неперервний варіант формулювання задачі

2) Характеристики до задачі рівномірного завантаження фізичних серверів.

Результати досліджень наведені на рис. 6. За ординату береться відношення величини ЦФ розв’язку до теоретично розрахованого оптимуму критерію, абсцисою є розмірність задачі — Сервери×Застосування. Характеристики будуються для обох варіантів математичної моделі:

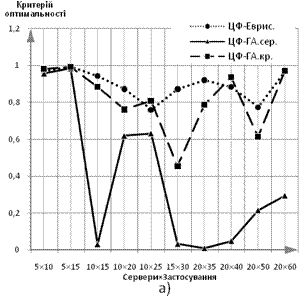
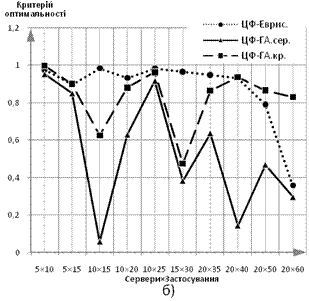
Рис. 6 Залежність значення ЦФ від розмірності вирішуваної задачі: а) дискретний варіант формулювання задачі,  б) неперервний варіант формулювання задачі

3) Характеристики до задачі мінімізації сумарних витрат на підтримку клієнтських запитів і реалізацію переходу до нового оптимального плану розміщення застосувань.

За ординату береться відношення величини ЦФ (вартості підтримки з урахуванням переходу) до сумарної вартості підтримки усіх серверів парку поточної конфігурації, абсцисою є розмірність задачі — Сервери×Застосування. Характеристики будуються для обох варіантів математичної моделі:

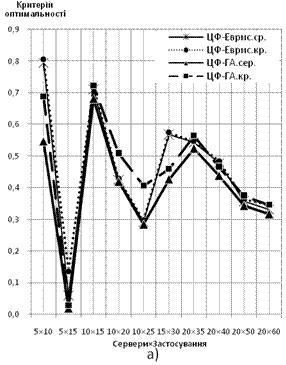
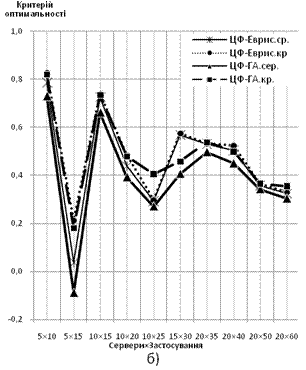
Рис. 7 Залежність значення ЦФ від розмірності вирішуваної задачі: а) дискретний варіант формулювання задачі б) неперервний варіант формулювання задачі

Характеристика порівняння оптимальності отриманих результатів для базового та керованого варіантів реалізації ГА — БГА і КГА відповідно (задача мінімізації витрат на підтримку запитів):

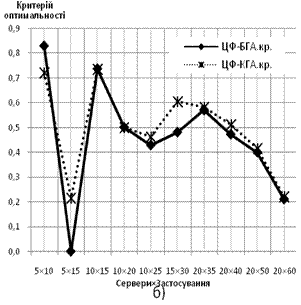
Рис. 8 Порівняння оптимальності розв’язків для БГА і КГА: а) середні значення оптимальності; б) кращі значення оптимальності

Як видно із ряду отриманих характеристик, використання керованого ГА дозволяє отримати покрашені результати відносно базового ГА. Варто зазначити, що у більшості випадків керований варіант отримував розв’язки швидше за кількістю епох за базовий ГА. У випадках, коли налаштуванням параметрів процес пошуку у керованого ГА збільшувався, одержаний результат у більшості випадків був оптимальнішим за варіант розв’язку базового ГА.

Таким чином, налаштовуючи систему правил керованого ГА, можна для кожної задачі підібрати схему значень, за якою за орієнтовну кількість кроків (епох) можна досягти розв’язку достатнього рівня оптимальності. Але пошук таких схем параметрів вимагає витрат часу та експериментальної роботи.

6 Особливості налаштування керованого ГА. Як вже було зазначено раніше, налаштування параметрів систему правил керованого ГА прямим чином впливають на якісні характеристики процесів у ньому. Для дослідження цього впливу побудуємо характеристики залежності кращого та середнього значень оптимальності розв’язку та кількості епох у залежності від значень параметрів.

Для прикладу розглянемо комбінований вплив зміни граничних швидкості збіжності та тиску відбору на оптимальність та швидкість протікання процесу пошуку для задачі мінімізації витрат на підтримку серверів (максимізації економії) при інших незмінних параметрах системи.

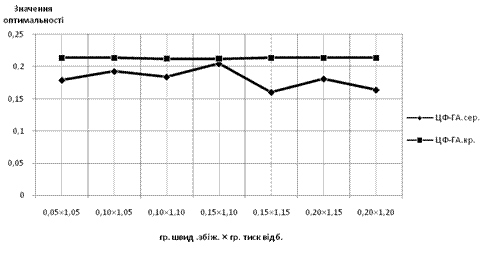
Рис. 9 Залежність показника оптимальності розв’язку від граничних значень швидкості збіжності та тиску відбору

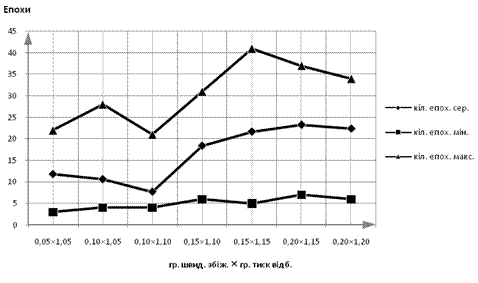
Рис. 10 Залежність кількості епох у процесі пошуку від граничних значень швидкості збіжності та тиску відбору

Суттєвий вплив на протікання процесів мають величини граничних швидкості збіжності та тиску відбору — оскільки визначають послідовність операцій кросоверу та мутацій. Дані величини будуть мати вплив на оптимальність отриманого розв’язку, а також на характер наближення до нього.

Величини критичних швидкості збіжності та тиску відбору впливають на момент зупинки пошуку оптимального рішення. Зменшуючи ці величини, можна досягти великої точності наближення до оптимуму за рахунок значного збільшення кількості епох у процесі пошуку. Слід зауважити, що при певних значеннях цих величин для певних задач процес пошуку може тривати нескінченно (якщо граничні значення фізично недосяжні, що випливає з формулювання ЦФ та наявних даних). Тому до регулювання цих параметрів слід ставитися дуже уважно, якщо процес пошуку має досягати кінцевого результату за скінчений проміжок часу.

Величина граничного приросту популяції впливає на частоту використання «вливання» додаткового генетичного матеріалу. Це опосередковано впливає, як на оптимальність знайденого розв’язку, так і на тривалість самого процесу пошуку.

Варто зауважити, що вплив кожного з розглянутих параметрів на хід процесу залежить у багатьох випадках від характеру самої задачі, поставленої перед алгоритмом, та особливостей математичних моделей даних, що ним використовуються. Таким чином, кожна із задач, поставлених перед алгоритмом, вимагає свого налаштування параметрів його системи правил.

Висновки. У статті запропонований варіант генетичного алгоритму, який відрізняється від відомих керуванням порядком виконання операторів.

Разом із розробленими авторами у циклі праць моделями і методами він покладений в основу реалізації функцій оптимізації створеної в НТУУ «КПІ» СУІ SmartBase.ITSControl. Ця система впроваджена у двох великих розподілених ІТС і використовується в декількох дослідно-конструкторських роботах, які перебувають на стадії проектування. Від попередніх технологій управління навантаженням і розподілом ресурсів СУІ SmartBase.ITSControl відрізняють надання адміністраторам можливості використовувати декілька критеріїв, врахування довільних типів абстрактних і конкретних ресурсів, гнучкість у переході до нових планів розміщення навантаження тощо.

Подальший розвиток досліджень пов’язаний з розробленням моделей і методів для інших моделей хостингу, що дозволить розширити множину ситуацій, в яких може застосовуватися створена СУІ SmartBase.ITSControl, та удосконаленням розроблених алгоритмів для підвищення її ефективності.

Перелік використаних джерел.

1.                  Павлов О.А. Інформаційні технології та алгоритмізація в управлінні / О.А.Павлов, С.Ф.Теленик. — К.: Техніка, 2002. — 344 с.

2.                  Теленик С.Ф. Определение распространения влияния неисправностей в сети доступа на качество предоставляемых сервисов / С.Ф. Теленик, А.И. Ролик, М.М. Букасов, М.В. Ясочка// Вісник НТУУ «КПІ». Інформатика, управління та обчислювальна техніка: Зб. наук. пр. — К.: Век+, — 2009. — №50. — С. 164 — 173.

3.                  Теленик С.Ф. Методы диагностики компонентов информационно-телекоммуникационных систем / С.Ф.Теленик, А.И. Ролик, Ю.С. Тимофеева //«Наукові вісті» Інституту менеджменту і економіки «Галицька академія». — Івано-Франківськ, 2009. — 1(15). — С. 49—58.

4.                  Ролик А.И. Управление устранением неисправностей в ИТ-системах / А.И. Ролик, Ю.С. Тимофеева, Н.И. Турский // Вісник НТУУ «КПІ». Інформатика, управління та обчислювальна техніка. — К.: «ВЕК+», — 2008. — № 49. — С. 94—107.

5.                  Теленик С.Ф. Управління ресурсами центрів оброблення даних / С.Ф.Теленик, О.І.Ролік, М.М.Букасов, К.О.Крижова // Вісн. Львів. ун-ту. Сер. прикл. матем. інформ. — Вип. 15. — 2009. — С. 325—340.

6.                  Теленик С. Управління навантаженням і ресурсами центрів оброблення даних при віртуальному хостингу / С.Теленик, О.Ролік, М.Букасов, С.Андросов, Р.Римар // Вісн. Тернопільського держ. техн. ун-ту. — 2009. — Том 14. — № 4. — С. 198—210.

7.                  Теленик С.Ф. Управління навантаженням і ресурсами центрів оброблення даних при виділених серверах/ С.Ф. Теленик, О.І. Ролік, М.М. Букасов, Р.В. Римар, К.О. Ролік // Автоматика. Автоматизація. Електротехнічні комплекси та системи. — Херсон, 2009. — № 2 (24). — С. 122—136.

8.                  Теленик С.Ф. Моделі і методи розподілу ресурсів в системах з серверною віртуалізацією / С.Ф. Теленик, О.І. Ролік, М.М. Букасов, О.А. Косован, О.І. Кобець // Зб. наук. праць ВІТІ НТУУ «КПІ».— №3.— К., 2009.— С.100—109.

9.                  Теленик С.Ф. Моделі управління розподілом обмежених ресурсів в інформаційно-телекомунікаційній мережі АСУ / С.Ф. Теленик, О.І. Ролік, М.М. Букасов // Вісник НТУУ «КПІ». Інформатика, управління та обчислювальна техніка. — К.: «Экотех». — 2006.— №44.— С. 234—239.

10.              Теленик С.Ф. Моделі управління віртуальними машинами при серверній віртуалізації / С.Ф. Теленик, О.І. Ролік, М.М. Букасов, А.Ю. Лабунський // Вісник НТУУ «КПІ». Інформатика, управління та обчислювальна техніка. — К.: «ВЕК+», — 2009.— № 51. — С. 150—155.

11.              Холланд Дж. Генетические алгоритмы / Дж. Холланд // В мире науки. — 1992.— №9—10.— С. 32—40.

12.              K.S. Leung, “A New Model of Simulated Evolutionary Computation — Convergence Analysis and Specifications”/ K.S. Leung, Q.H. Duan, Z.B. Xu, and C. K. Wong// IEEE Transactions on Evolutionary Computation, Vol. 5, No. 1. — February, 2001 — P. 3—16.