УДК 681.3
МОДИФИЦИРОВАННЫЙ РЕКУРРЕНТНЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
С СУПРЕМАЛЬНЫМИ СВОЙСТВАМИ
Тимофеев В.А.
Введение. На сегодня проблема управления техническим объектом в условиях неопределенности – одна из центральных проблем современной теории управления. Адекватным математическим аппаратом для решения этой проблемы является теория адаптивных систем управления, а широкое распространение микропроцессорной техники привело к развитию дискретных адаптивных систем управления [1-16].
К настоящему времени сформировался ряд относительно независимых направлений в теории адаптивных систем. Здесь, прежде всего, следует выделить адаптивные регуляторы с минимальной дисперсией (основополагающая работа [17]), адаптивные регуляторы с обобщенной минимальной дисперсией (основополагающие работы [18,19]), адаптивные системы с требуемым размещением нулей и полюсов (основополагающие работы [19-21]), системы с адаптивными упредителями (основополагающая работа [22]).
Во всех этих подходах предполагается, что возмущения, действующие в системе, имеют стохастическую природу, причем это, как правило, белый шум с нулевым математическим ожиданием и ограниченной дисперсией. В практических ситуациях статистические предпосылки являются надуманными, в связи с чем гораздо более реальными представляются допущения лишь об ограниченности шума или его разностей по амплитуде. В этих условиях использование методов идентификации, основанных на квадратичных критериях и, прежде всего, рекуррентного метода наименьших квадратов явно неэффективно. Возникающие затруднения частично могут быть преодолены в рамках адаптивных робастных систем управления [23-26], в которых, тем не менее, все равно «спрятаны» определенные статистические предпосылки.
В связи с этим представляется целесообразным осуществить синтез теории адаптивного и критического управления, что приведет к созданию адаптивных супремальных методов контроля, идентификации и управления динамическими объектами, функционирующими в условиях существенной неопределенности о характеристиках объекта и окружающей среды.
Целью настоящей работы и является разработка рекуррентного метода идентификации, обеспечивающего получение оценок, обладающих супремальными свойствами, которые не зависят от статистических характаристик сигналов и помех, и свойствами МНК-оценок.
Постановка задачи. Рассмотрим динамический
объект, функционирующий в замкнутой системе управления ![]() ,
описываемый разностным уравнением
,
описываемый разностным уравнением
![]() , (1)
, (1)
где полиномы ![]() с
с ![]() ;
; ![]() - время чистого запаздывания
- время чистого запаздывания ![]()
![]() и
и ![]() - выходной, управляющий и возмущающий
сигналы соответственно.
- выходной, управляющий и возмущающий
сигналы соответственно.
Относительно возмущений предполагается ограниченность их первых разностей.
В случае, если параметры объекта априори известны и неизменны, задача критического управления может быть решена с помощью супремального регулятора, т.е.
![]() (2)
(2)
где полиномы ![]() с
с ![]() и
и ![]() задаются уравнением
задаются уравнением
![]()
В том случае, если параметры объекта неизвестны, можно воспользоваться тем или иным методом идентификации, а затем применить закон управления (2), в котором истинные значения параметров объекта заменены их оценками. В этом и состоит суть адаптивного подхода к проектированию систем управления объектами, функционирующими в условиях неопределенности. Как правило, в качестве процедур идентификации те или иные модификации рекуррентного метода наименьших квадратов либо проекционные алгоритмы, так или иначе связанные с квадратичными критериями. При использовании критериев, отличных от квадратичных, например, модульных, хотя и получают робастные процедуры, статистический смысл задачи идентификации тем не менее сохраняется. Естественно, что такие алгоритмы идентификации не могут быть использованы в критических системах управления.
В связи с этим возникает необходимость синтеза адаптивных алгоритмов идентификации, не связанных ни с какими статистическими предпосылками, обладающих высокой скоростью сходимости, вычислительной простотой и пригодных для работы в реальном времени в контуре критической системы управления динамическим объектом.
Алгоритмы идентификации, применяемые в критических системах. Введем в рассмотрение полином
![]() (3)
(3)
где ![]() ,
,
и перепишем уравнение объекта (1) в виде
![]() (4)
(4)
где ![]()
![]()
![]()
![]()
Тогда задача идентификации с позиции теории критических систем
сводится к нахождению оценок неизвестного вектора параметров ![]() таких, что
таких, что
![]() . (5)
. (5)
Здесь ![]() - оценка параметра
- оценка параметра ![]() .
.
К настоящему времени сложился ряд подходов к задаче идентификации, связанной с неравенством (5). Это, прежде всего, подход Фогеля-Хуанга [27], в основе которого лежат некоторые геометрические построения. Известна также процедура Лозано-Лила-Ортеги [28], синтезированная как на геометрических предпосылках, так и исходя из условий устойчивости процесса сходимости. Нельзя не отметить также алгоритм Канудас де Вита-Каррильо [29], являющийся некоторой модификацией экспоненциально взвешенного рекуррентного МНК. Несмотря на эффективность этих процедур, их использование в критических системах наталкивается на серьезные затруднения.
Так, оптимальный алгоритм Фогеля-Хуанга настолько сложен с
вычислительной точки зрения, что не может быть и речи о его использовании в
режиме реального времени. Эта сложность обусловлена, прежде всего,
необходимостью отыскания на каждой итерации глобального минимума
многоэкстремальной функции ![]() переменных, что само
по себе является достаточно сложной проблемой.
переменных, что само
по себе является достаточно сложной проблемой.
В алгоритме Лозано-Лила-Ортеги, имеющем вид
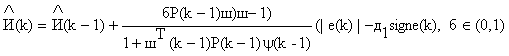 ; (6)
; (6)
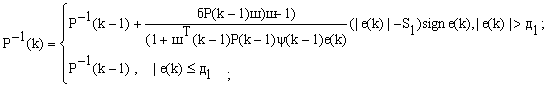 (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
априори
предполагается ограниченность значения ![]() ,
из которого следует условие сходимости
,
из которого следует условие сходимости
![]()
т.е. ошибка
идентификации ![]() никогда не может быть по
модулю меньше заданных ограничений
никогда не может быть по
модулю меньше заданных ограничений ![]() .
.
В алгоритме Канудас де Вита-Каррильо
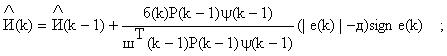 (10)
(10)
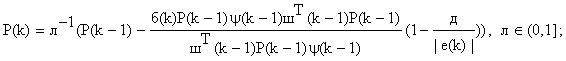 (11)
(11)
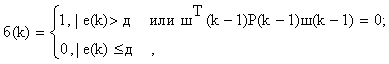 (12)
(12)
где ![]() определяется соотношением (9),
определяется соотношением (9),
![]()
в ситуации, когда ![]() и значение
и значение ![]() близко
к нулю, возникает режим неустойчивости, поскольку компоненты вектора
близко
к нулю, возникает режим неустойчивости, поскольку компоненты вектора
![]()
могут неограниченно
возрастать. Кроме того, в случае, когда ![]() ,
невозможно гарантировать выполнение условия
,
невозможно гарантировать выполнение условия ![]() в
предположении, что
в
предположении, что ![]() ограничено.
ограничено.
Модифицированный алгоритм идентификации и оценивание его сходимости. Объединяя достоинства рассмотренных процедур, можно ввести комбинированный алгоритм, являющийся своеобразной комбинацией рекуррентного МНК и процедур (6)-(8) и (10)-(12).
Рассмотрим алгоритм вида
![]()
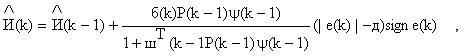 (13)
(13)
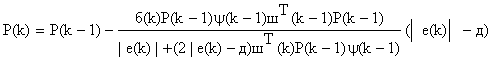 , (14)
, (14)
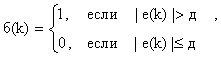 (15)
(15)
где ![]() определяется в соответствии с (9),
и проанализируем его сходимость.
определяется в соответствии с (9),
и проанализируем его сходимость.
Введем в рассмотрение вектор уклонений оценок от истинных значений параметров
![]()
и функцию Ляпунова
![]()
Объединяя (4) с (13)-(15), получаем
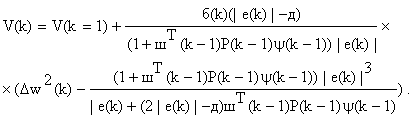 (16)
(16)
С учетом ранее введенного условия ![]() несложно
переписать (16) в виде неравенства
несложно
переписать (16) в виде неравенства
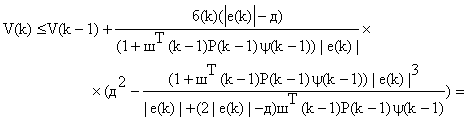
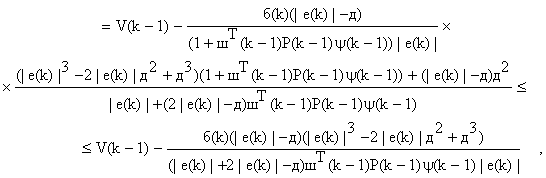
которое справедливо
в случае ![]() Кроме того, поскольку в этом случае
Кроме того, поскольку в этом случае
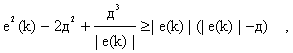
несложно видеть, что
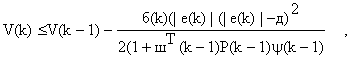 (17)
(17)
откуда
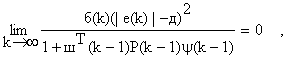 (18)
(18)
что свидетельствует о критериальной сходимости алгоритма (13)-(15).
Перенеся в левую часть (13) ![]() и возведя обе части
полученного выражения в квадрат, получаем
и возведя обе части
полученного выражения в квадрат, получаем
![]()
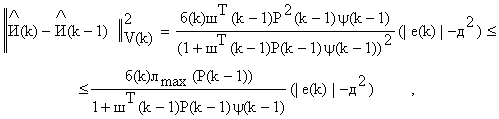 (19)
(19)
где ![]() - максимальное собственное значение
матрицы
- максимальное собственное значение
матрицы ![]()
![]() .
.
Из (14) очевидно следует условие
![]()
позволяющее переписать (19) в виде
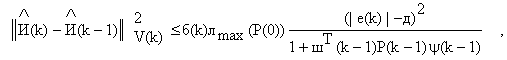
который вместе с выражением (18) свидетельствует об аргументной сходимости алгоритма.
Далее, используя лемму об обращении матриц, запишем
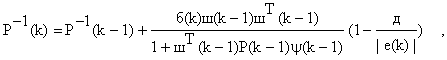
откуда следует неравенство
![]()
где ![]() - минимальное собственное значение
матрицы
- минимальное собственное значение
матрицы ![]() .
.
Это неравенство совместно с (17) приводит к тому, что
![]()
и
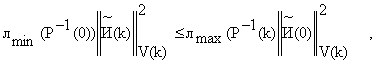
откуда можно записать выражение
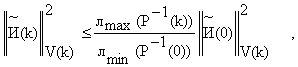
определяющее скорость сходимости введенного алгоритма.
Выводы.
В работе предложена модификация рекуррентного МНК, обладающая супремальными
свойствами. Так как основой данного алгоритма является рекуррентный МНК, трудностей
с его практической реализацией не возникает. Полученная оценка скорости сходимости
предложенного алгоритма свидетельствует о том, что эта скорость в значительной
мере определяется свойствами ковариационной матрицы наблюдений ![]() ( соотношением ее максимального и минимального собственных чисел).
Кроме того, входящая в алгоритм величина
( соотношением ее максимального и минимального собственных чисел).
Кроме того, входящая в алгоритм величина ![]() зачастую
известна лишь приближенно, поэтому необходимо в процессе идентификации
осуществлять оценивание (уточнение) этой величины и подставлять полученные
оценки в алгоритм идентификации.
зачастую
известна лишь приближенно, поэтому необходимо в процессе идентификации
осуществлять оценивание (уточнение) этой величины и подставлять полученные
оценки в алгоритм идентификации.
|
In work updating of a recurrent method of the least squares, having supremal properties, is offered. The offered recurrent method of identification provides reception of estimations which do not depend on statistical characteristics of signals and handicapes. |
1. Isermann R. Practical aspects of process identification // Automatica.-1980.-16.-P. 575-597.
2. Evans R. J., Betz R. E. New results and applications of adaptive control to classes of nonlinear systems // Ricerche di Automatica.-1982.-13.-№2.-Р. 277-297.
3. Tsypkin Y. Z. The theory of adaptive and learning systems // Cybern.:Theory and Appl. - Washington, D. C., 1983.- P. 59-89.
4. Astr6m K. J. Theory and Applications of adaptive control - a survey // Automica.- 1983.-19.-№5.-Р. 471-486.
5. Цыпкин Я. 3., Кельманс Г. К. Дискретные адаптивные системы управления // Итоги науки и техники. Техн. кибернетика. - Т. 17.-М.: ВИНИТИ, 1984.-С. 3-73.
6. Navendra К. S., Annaswamy A. M. Recent trends in adaptive control theory // J. Soc. Instrum. And Control Eng.- 1984.-23-.No5.-P. 27-34.
7. Kumar P. R. A survey of some results in stochastic adaptive control // SIAM J. Control and Optim.-1985.-23-№3.- Р. 329-380. Unbehauen H. Theory and application of adaptive control // Ргос. 7th IFAC/ IMACS Conf. -Vienna.- 1985.-P. 1-17.
8. Иванов В. А., Шапировский M. P. Адаптивные системы управления с моделями // Итоги науки и техники. Техн. кибернетика. -Т.18.-М.: ВИНИТИ, 1986.-С. 210-240.
9. King-Sun Fu. Learning control systems - Review and outlook // IEEE Trans. on Pattern Anal. and Mach. Intel.-1986.-8.-Mo3.-P. 327-342.
10. De Keyser R. M. C. Applying adaptive control problems and solutions // Journal A. - 1986.-27.-№3.- Р. 111-119.
11. Martin Sanchez J. M. Adaptive control for time - variant processes // Int. J. Contr.- 1986.-44.-№2.-Р. 315-329.
12. Кунцевич В.М. Адаптивное управление: алгоритмы, системы, применение . -К.: Выща шк., 1988.- 64 с.
13. Александров А. Г. Оптимальные и адаптивные системы. - М.:Высш. шк., 1989.-263с.
14. Романенко В. Д., Игнатенко Б. В. Адаптивное управление технологическими процессами на базе микроЭВМ. - К.: Выща шк., 1990.-334с.
15. Astr6m К. J., Wittenmark В. On self-tuning regulators // Automatica.-1973.-9.-P.185-199.
16. Clarke D. W., Gawthrop P. J. Self-tuning controller// Proc. IEE.-1975.-122.-P. 929-934.
17. Wellstead P. E., Edmunds М. J., Prager D., Zanker P. Self-tuningpole/ zero assignment regulators // Int. J. Contr.-1979.-30.-№1.- Р. 1-26.
18. Wellstead P. E., Prager D., Zanker P. Pole assignment self-tuning regulator // Proc. DEE.-1979.-126.-D.- P. 781-787.
19. Astrom K. J., Wittenmark B. Self-tuning controllers based on pole-zero placement // Proc. IEE.-1980.-127.-D.- P. 120-130.
20. Kreisselmeier G., Narendra K. S. Stable MRAC in the presence of bounded disturbances // IEEE Trans. on Autom. Contr.-1982.-27.- P. 1169-1175.
21. Clarke D. W., Mohtadi C., Tuffs P. S. Generalized predictive control. Tue basis algorithm // Automatica.-1987.- 22.- №2.- P. 137-148.
22. Samson С. Stability analysis of adaptively controlled systems subject to bounded disturbances // Automatica.- 1983.-19.- P. 81-89.
23. Narendra K. S., Annaswamy A. М. Robust adaptive control in the presence of bounded disturbances // IEEE Trans. on Autom. Contr.-1986.-31.-№4.-P.306-315.
24. 0rtega R., Lozano-Leal R., A note on direct adaptive control of systems with bounded disturbances // Automatica.-1987.-23.- №2.- P. 253-254.
25. Fogel E., Huang Y. F. On the value of information in system identification - bounded noise case // Automatica. -1982.-18.-№2.- Р. 229-238.
26. Lozano-Leal R., Ortega R. Reformulation of the parameter identification problem for system with bounded disturbances //Automatica.- 1987.-23.- №2.- P. 245-257.
27. Canudas de Wit C.C., Carrilo J. A modified EW - RLS algorithm for systems with bounded disturbances // Automatica.-1990.- 26.- P. 599-606.
28. Фомин В. Н. Математическая теория обучаемых опознающих систем. - Л.: Изд. ЛГУ, 1976. – 235 c
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.