УДК 004.942.001.57:621.1

         Постановка задачи

       Установки теплоснабжения, использующие нетрадиционные источники энергии являются перспективными с точки зрения экономии ресурсов топлива и снижения вредного воздействия на окружающую среду. Для увеличения срока эксплуатации, экономичного использования тепла и топлива, эффективной работы установки необходимо применение средств автоматизации. Одна из таких установок, представленная в [1], как объект управления ранее не рассматривалась.

       Путь решения задачи

         Для автоматизированного управления установкой теплоснабжения необходимо знать свойства этой установки в целом и отдельных её элементов. В данной статье рассмотрены модели отдельных элементов установки теплоснабжения в линейном приближении.

Структурная схема установки теплоснабжения изображена на рис. 1.

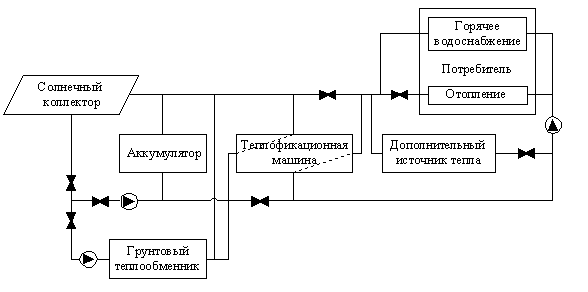
Рис. 1 Структурная схема установки теплоснабжения

Установка теплоснабжения состоит из следующих элементов:

–– солнечный коллектор;

–– аккумулятор тепла;

–– грунтовый теплообменник;

–– помещение потребителя;

–– дополнительный источник тепла;

–– теплофикационная машина.

Основным элементом рассматриваемой установки является плоский солнечный коллектор. Структурная схема солнечного коллектора представлена на рис. 2.

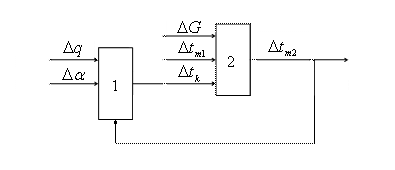
Рис. 2 Структурная схема солнечного коллектора

Солнечный коллектор условно разбит на два звена.

Звено 1 – отражает связь между удельным тепловым потоком солнечной инсоляции , коэффициентом теплоотдачи от стенки солнечного коллектора к теплоносителю , который является функцией скорости теплоносителя, температурой теплоносителя на выходе солнечного коллектора  и температурой стенки солнечного коллектора .

Звено 2 – отражает связь между расходом теплоносителя через солнечный коллектор , температурами теплоносителя на входе солнечного коллектора , стенки солнечного коллектора и температурой теплоносителя на выходе солнечного коллектора .

Исходя из приведённой структурной схемы и теплового баланса для рассматриваемого элемента установки, была получена система дифференциальных уравнений, которая устанавливает связь между указанными параметрами:

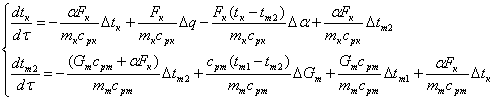             ,              (1)

где ,  – площади теплообмена со стороны теплового потока от солнца и стенки солнечного коллектора, соответственно;

,  – массы солнечного коллектора и теплоносителя, соответственно;

,  – удельные теплоёмкости стенки солнечного коллектора и теплоносителя, соответственно;

 –изменение соответствующей величины.

Переходя к описанию свойств солнечного коллектора в матричной форме записи динамических систем [2], были получены следующие матрицы:

, , , ,

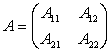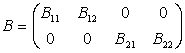где: , , , , , , , .

Следующим элементом установки является аккумулятор тепла. Для рассматриваемой установки теплоснабжения выбран аккумулятор теплоты емкостного типа для краткосрочного аккумулирования. Параметрическая схема бака-аккумулятора тепла изображена на рис. 3.

Рис. 3 Параметрическая схема бака-аккумулятора тепла

Температура в аккумуляторе  зависит от температуры теплоносителя на входе в аккумулятор . На основе данной схемы и теплового баланса для бака-аккумулятора получено дифференциальное уравнение:

                                                       ,                                                      (2)

где  – расход теплоносителя, проходящего через аккумулятор;

 – масса конструкции аккумулятора.

Для описания свойств рассматриваемого аккумулятора в матричной форме записи динамических систем были получены следующие матрицы:

, , , ,

где: , .

Следующим элементом установки теплоснабжения является грунтовый теплообменник. Поле грунтовых теплообменников является источником тепловой энергии либо аккумулятором тепловой энергии в зависимости от температур теплоносителя и грунта. Поле грунтовых теплообменников – набор трубок Фильда, расположенных в грунте на некотором расстоянии друг от друга. Грунтовый теплообменник-аккумулятор представляет собой трубку Фильда погруженную в грунт. Расчётная схема теплообменника приведена на рис.4 а). Теплообменник можно представить в виде цилиндра диаметром  и высотой . Структурная схема грунтового теплообменника представлена на рис. 4 б).

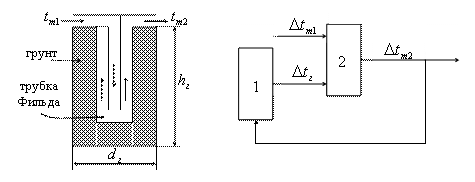
а)                                            б)

Рис. 4 Расчётная (а) и структурная (б) схемы грунтового теплообменника

Грунтовый теплообменник условно разбит на два звена.

Звено 1 – отражает связь между температурой теплоносителя на выходе грунтового теплообменника  и температурой грунта .

Звено 2 – отражает связь между температурами объёма грунта теплообменника , теплоносителя на входе теплообменника  и температурой теплоносителя выходе .

Система дифференциальных уравнений, полученная из структурно-параметрической схемы и теплового баланса для рассматриваемого элемента установки, устанавливает связь между указанными параметрами:

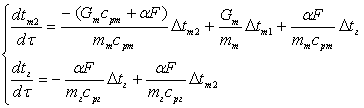                              ,                              (3)

где  – расход теплоносителя;

,  – удельные теплоёмкости теплоносителя и грунта теплообменника, соответственно;

,  – массы теплоносителя, проходящего через теплообменник, и объёма грунта теплообменника, соответственно;

 – коэффициент теплоотдачи от теплоносителя к объёму грунта теплообменника;

 – площадь теплообмена со стороны теплоносителя.

Переходя к описанию свойств грунтового теплообменника в матричной форме записи динамических систем, были получены следующие матрицы:

, , , ,

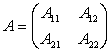где: , , , , .

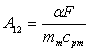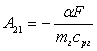При этом были приняты следующие обозначения:

В качестве следующего элемента установки теплоснабжения рассмотрим помещение потребителя. Для данной установки теплоснабжения рассматривается помещение жилого дома. Параметрическая схема помещения изображена на рис. 5.

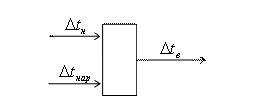
Рис. 5 Параметрическая схема помещения потребителя

Помещение представляет собой прямоугольную комнату с окном площадью , стенами общей площадью  и установленным нагревателем с площадью теплообмена . Данная схема отражает связь между температурами окружающей среды , поверхности нагревателя  и воздуха в помещении .

Приведённая схема и тепловой баланс для помещения потребителя являются основой для полученного дифференциального уравнения, которое устанавливает связь между указанными параметрами:

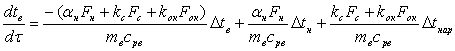                  ,                   (4)

где  – масса воздуха в помещении;

 – удельная теплоёмкость воздуха в помещении;

 – коэффициент теплоотдачи от нагревателя воздуху в помещении;

,  – коэффициенты теплопередачи через стену и окна помещения, соответственно.

Матрицы, полученные при переходе к описанию свойств солнечного коллектора в матричной форме записи динамических систем, имеют следующий вид:

, , , ,

где: , , .

Следующий элемент рассматриваемой установки теплоснабжения – дополнительный источник тепла, в качестве которого выбран водогрейный котёл на газообразном топливе. Динамические свойства таких котельных агрегатов достаточно подробно описаны в [3, 4, 5, 6].

Приведённые матрицы элементов установки теплоснабжения можно объединить в единую систему матриц. Однако, структура полученной системы является переменной и зависит от режима работы установки теплоснабжения.

Выводы

Рассмотренные модели позволяют составить обобщённую модель установки теплоснабжения при различных видах взаимосвязей между данными элементами, что позволит синтезировать систему оптимального управления установкой теплоснабжения.

           The heat supply system uses the alternative power sources (solar – ground). It consists from the elements. The mathematics models of the elements are described in this paper. These models let write the generalized model of the heat supply system at various kind of conduction between the elements. These models can be used for at synthesizing a regulator of optimum control by such system.

1.                  Денисова А.Е., Тодорцев Ю.К., Максименко И.Н. К вопросу об автоматизации интегрированной установки теплоснабжения с возобновляемыми источниками энергии // АЭКС. – 2004. – № 2 (14). – С. 227 – 231 .

2.                  Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами: Учебник для вузов. – М.: Энергоатомиздат. 1985. – 296 с., ил.

3.                  Демченко В.А. Автоматизация и моделирование технологических процессов АЭС и ТЭС.: Учебное пособие. – Одесса: Астропринт, 2001. – 306 с., ил.

4.                  Профос П. Регулирование паросиловых установок. – М.: Энергия, 1967. – 368 с.

5.                  Чермак И., Петерка В., Заворка И. Динамика регулируемых систем в теплоэнергетике и химии. – М.: Мир, 1972. – 623 с.

6.                  Остапенко Ю.О. Ідентифікація та моделювання технологічних об’єктів керування. – К.: Задруга, 1999. – 422 с.