Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК    378.147:044.4’24(477)

МОДЕЛИ ЗАДАЧИ РАСПРЕДЕЛЕНИЯ В ТЕОРИИ РАСПИСАНИЯ

Ускач А.Ф., Гогунский В.Д., Яковенко А.Е.

Большинство задач теории расписаний в общей постановке весьма привлекательны в силу их кажущейся простоты. Однако достижение даже небольшого прогресса на пути их решения связано, как правило, с огромными теоретическими и практическими трудностями. С точки зрения теории сложности, большинство задач теории расписаний относится к классу NP-сложных задач, требующих для своего решения разработки эвристических (приближенных) алгоритмов, учитывающих специфику рассматриваемой в задаче предметной области.

В теории расписаний основное внимание уделяется вопросам оптимального распределения и упорядочения конечного множества требований, обслуживаемых детерминированными системами с одним или несколькими приборами, при различных предположениях относительно характера их обслуживания.

В качестве приборов могут вычислительные машины, учебные помещения, преподаватели и т.п., в качестве требований – обрабатываемые детали, выполняемые программы, поезда, группы студентов и т.п.

При планировании учебного процесса могут быть выделены такие "блоки", как преподаватели, осуществляющие определенные работы по обучению студентов, учебные группы студентов, воспринимающие определенную информацию и т.д.
Теория расписаний решает три класса задач – задачи упорядочения, распределения и согласования. Задача закрепления преподавателей за группами студентов и распределения учебных помещений принадлежит к классу распределительных задач [1].

Многокритериальность задачи составления расписания и сложность объекта, для которого сроится математическая модель, обуславливает необходимость серьезного математического исследования объекта для увеличения функциональных возможностей алгоритмов составления расписаний без значительного усложнения модели и, как следствие, увеличения объемов используемой памяти и времени решения задачи.

В данной статье рассматриваются методы построения моделей задачи распределения в теории расписания для определения наиболее применимого метода.

            1. Линейная модель. Построим математическую модель задачи распределения на примере расписания  вуза в терминах линейного программирования: имеется N учебных групп, занятия проводятся в рабочие дни в полуторачасовые интервалы, которые будем называть парами. Пусть t – номер рабочего дня недели, t Є T_n, где T_n – множество номеров рабочих дней для группы n є N; j – номер пары, j = 1 ,…, J, где J – общее количество пар. С каждой учебной группой n в течение недели, согласно учебному плану, проводится W_n занятий.

Предположим p – номер (имя) преподавателя, p = 1 ,…, P. Введем в рассмотрение булево значение :

1, если в группе n занятие wn проводит преподаватель p; 0 – в противном случае;

Учебная нагрузка преподавателей планируется до составления расписания занятий, вследствие чего на данном этапе величину  можно считать заданной. Для каждого преподавателя p, p = 1 ,…, P  задана также его аудиторная нагрузка  –  N_p часов в неделю.

Задача составления расписания заключается в определении для каждого занятия дня недели и пары в этот день с учетом выполнения конструируемых ниже ограничений и минимизации некоторой целевой функции.

Введем следующие искомую булеву переменную:

1, если в группе n в день t на паре j проводится занятие wn 0 – в противном случае;

= 

Ограничения: для каждой группы n должны выполняться все аудиторные работы в течение недели:

(1)

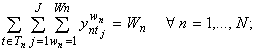
В любой день t на каждой паре j для каждой группы n может проводиться не более одного занятия:

(2)

                

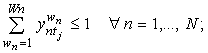
Каждые занятие w_n соответственно для всех групп n может проводиться не более одного раза в любой день t:

(3)

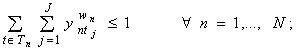
Если переменная увязывают все виды занятий с временем их проведения, то произведение  связывает время проведения с именем преподавателя.

В каждый день t и в каждой паре j преподаватель p может вести не более одного занятия по одной дисциплине в одной группе:

(4)

(5)

Каждый преподаватель p в течение недели должен провести аудиторные занятия:

Представленными соотношениями исчерпываются безусловные ограничения, с которыми всегда считаются при составлении расписания. Могут, однако, быть и специфические условия, прежде всего проведение отдельных видов работы по “верхней” или по “нижней” неделе (т.е. один академический час в неделю). Не исключены и другие специальные условия, но для упрощения модели они не рассматривались.

Целевая функция: рассмотрим выражение для величины аудиторной нагрузки в день t преподавателя p:

(6)

(7)

Вводятся ограничения вида:

где M – произвольное положительное достаточно большое число;  – искомая булева переменная.

Из (7) вытекает, что если , то  = 1, и если , то  = 0.

С учетом указанного выше содержательного смысла критерия оптимизации в дополнительных ограничениях (7), а также вводя весовые коэффициенты статуса преподавателя (его ученые степени и звание, занимаемая должность, научно-общественная активность), получаем искомый критерий оптимальности:

(8)

Введенная целевая функция не является единственно возможной. Введение других целевых функций не меняет ограничений математической модели и методов решения задачи, но может существенно повлиять на результаты вычислений.

Поставленная задача максимизации линейной целевой функции при заданной системе ограничений является задачей линейного целочисленного булева программирования, поскольку все коэффициенты ограничений целочисленные в силу дискретности исходных данных задачи; кроме этого искомые переменные математической модели могут принимать только два значения.

К наиболее широко используемым приемам сокращения перебора относятся приемы, основанные на методе ветвей и границ или на методе неявного перебора. Эти приемы состоят в построении «частичных решений», представленных в виде дерева поиска и применении методов построения оценок, позволяющих отсекать бесперспективные частичные решения. [1]

Другой подход – использование модификации симплекс-метода для случая задачи целочисленного линейного программирования [2].

    Однако большая размерность данной задачи теории расписания и содержание значительного числа булевых переменных приводит к неизбежности экспоненциальности времени решения задачи не зависимо от выбора метода решения.

2. Комбинаторный подход сводится к целенаправленной перестановке пар работ в некоторой исходной последовательности, пока не будет получено оптимальное (близкое к оптимальному) решение. Сформулируем задачу распределения: пусть задано множество N групп учебного заведения, в которых работают множество Р = {1, 2,…, p} преподавателей. Длительности t_iL, i = 1, … , p, L = 1, … , N, работ преподавателей в группах одинаковы (время проведения занятия). Не нарушая общности рассуждений, их можно считать равными единице. Необходимо построить расписание занятий без наличия «окон», при условии минимизации суммы моментов завершения распределения нагрузки преподавателей. Но так как некоторые t_iL = 0 (не во всех группах у преподавателей есть нагрузка), то задача минимизации суммарного времени работы оказывается NP-трудной, что доказывается путем сведение ее к задаче о трехцветной раскраске 4-регулярного графа: дан неориентированный граф G =  (X,U) без петель, степень каждой вершины которого равна четырем. Можно ли раскрасить вершины графа G в три цвета таким образом, что никакие две смежные вершины не окрашиваются в один цвет?

Рассмотрим соответствующую задачу распознавания: определить, существует ли расписание s⁰ (как с «окнами», так и без «окон») такое, что  ( –суммарное время работы преподавателей ) для заданного y.

Положим к примеру p = 95 |X| + 5 |U|, P = {1, 2,.., p}; n=25 |X| +5 |U|, N = {1, 2,.., n}. Так как число ребер произвольного графа равно полусумме степеней его вершин и по условию граф G 4-регулярный, заключаем, что |U|=2 |X|, т. е. p = 3n.

Множество N приборов разобьем на два подмножества N(U) и N(X). Первое подмножество содержит 5|U| групп, соответствующих ребрам u_k є U графа G и обозначаемых U_l(k), 1 ≤ l ≤ 5, 1 ≤ k ≤ |U|. Второе подмножество состоит из 25|X| групп, соответствующих вершинам x_j  є X графа G и обозначаемых X_lq(j), 1 ≤ l ≤ 5, 1 ≤ q ≤ 5, 1 ≤ j ≤ |X|.

Множество P преподавателей разобьем на три подмножества P(W), P(U), P(X).

Множество P(W) преподавателей состоит из 25|X| преподавателей обозначаемых w_lq(j), 1 ≤  l ≤ 5, 1 ≤ q ≤ 5, 1 ≤ j ≤ |X|. Если в графе G вершине x_j инцидентны ребра u_k1, u_k2, u_k3, u_k4, то преподаватель w_lq(j), 1 ≤ l ≤ 5, 1 ≤ q ≤ 5, работает в четырех группах U₁(k₁), U₁(k₂), U₁(k₃), U₁(k₄)  из множества N(U), а также в группе X_lq(j) и не работает во всех других группах.

Множество P(U) преподавателей состоит из 5 |U| преподавателей, соответствующих ребрам u_k графа G и обозначаемых u_m(k), 1 ≤ m ≤ 5, 1≤ k ≤ |U|. Преподаватель u_m(k) работает только в пяти группах вида u_l(k), 1 ≤ l ≤ 5.

Множество P(X) преподавателей состоит из 70|X| преподавателей, соответствующих вершинам x_j графа G и обозначаемых x_lm(j), 1 ≤ l ≤ 5, 1 ≤ m ≤ 14, 1 ≤ j ≤ |X|. Преподаватель x_lm(j),работает в пяти группах x_lq(j), 1 ≤  q ≤ 5.

Таким образом, каждый преподаватель множества Р должен работать ровно в пяти группах.

В результате дальнейших рассуждений можно показать, что задача о 3-раскраске 4-регулярного графа имеет решение тогда и только тогда, когда в построенной задаче существует расписание s⁰ такое, что  [1].

Поскольку задача о трехцветной раскраске 4-регулярного графа NP-полна и реализация ее сведена к рассматриваемой задаче распознавания путем выполнения полиномиального (относительно |X| ) числа операций, то задача построения расписания, минимизирующего суммарное время работы, в случае, когда все t_iL є {0,1}, является NP-трудной.

3. Сетевое представление. Зададим дополнительные условия в постановке задачи расписания (множество {1, 2,…, L, … , M} групп учебного заведения, в которых работают множество N = {1, 2, … , n} преподавателей, длительности работы преподавателя в группе соответствует одному занятию): преподаватель k є N проводит занятия в группах в определенном порядке (). Количество групп ,  для каждого преподавателя отвечает его нагрузке, т. е.  не обязательно различны.

Т. к. на практике порядок () не является заданным, то данное условие предполагает, используя элементы комбинаторики, определить число Р комбинаций перестановок последовательностей (), k є N:

Полученное число говорит о количестве вариантов условий поставленной задачи.

Введем понятие операции как процесса проведения преподавателем занятия в группе. Т. е. процесс работы преподавателя k состоит в последовательном проведении занятий в r_k группах. Если преподаватель k проводит занятие в группе L в q-й по очереди раз, то эту операцию будем обозначать через (k, L, q), а длительность ее выполнения через t( k, L, q).

Представим все операции в виде точек (кружков) на плоскости. Каждые две операции  (k₁, L₁, q₁) и (k₂, L₂, q₂) могут быть зависимы или независимы в том смысле, что календарное время выполнения одной из них оказывает или не оказывает влияние на календарное время выполнения другой. В условиях рассматриваемой задачи целесообразно выделить три вида бинарных межоперационных отношений.

Если k₁ ≠ k₂ и L₁ ≠ L₂, то операции (k₁, L₁, q₁) и (k₂, L₂, q₂) являются независимыми. Графически они не соединяются никакими видами связей – ребрами, дугами и т. п.

Если k₁ = k₂ = k, то по условию задачи одна из операций, для определенности, (k₁, L₂, q₂) следует во времени за второй. В данном случае операция (k, L₂, q₂) не может быть начата раньше, чем закончится операция (k, L₁, q₁). Графически операции (k, L₁, q₁) и (k, L₂, q₂) соединяются дугой, направленной от первой операции ко второй.

Если L₁ = L = L и k₁ ≠ k₂, то операции (k₁, L, q₁) и (k₂, L, q₂) не могут выполняться одновременно, однако очередность их выполнения заранее не оговорена. В этом случае соединим операции ребром.

В результате получаем смешанный граф (X, , U), где X – множество операций (вершин), – множество дуг, U – множество ребер. На рис. 1 изображен смешанный граф для 4-х групп и 3-х преподавателей.

Каждое допустимое расписание определяет календарные сроки проведения каждой операции и тем самым однозначно фиксирует определенные последовательности выполнения операций в каждой группе. Иными словами, каждому расписанию соответствует некоторый ориентированный бесконечный граф, порождаемый данным смешанным графом в результате замены всех его ребер дугами.

Каждый бесконтурный ориентированный граф определяет бесконечное число (допустимых) расписаний. Действительно, если приписать каждой дуге этого графа, соединяющей вершину (k₁, L₁, q₁) с вершиной (k₂, L₂, q₂), число t(k₁, L₁, q₁) – длительность операции (k₁, L₁, q₁). В результате получим сетевой график. Используя обычную технику сетевого планирования, можно определить время начала и окончания каждой операции, т. е. построить расписание проведения преподавателями занятий в группах. Таких расписаний, очевидно, можно построить сколь угодно много.

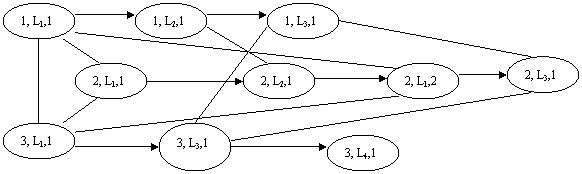 Рис. 1 Смешанный граф для 4-х групп и 3-х преподавателей

Для построения сетевого графика можно воспользоваться следующей процедурой:

а) в списке операций выбираем одну из операций, которая не следует ни за одной операцией списка;

б) заменяем все ребра в рассматриваемом смешанном графе, соединяющие выбранную операцию и другие операции списка, на исходящие из соответствующей ей вершины дуги. Удаляем операцию из списка;

в)  если список операций исчерпан, процедура окончена, в противном случае переходим к пункту а).

Выбирая в п. а) различные операции, получаем в результате многократного применения данной процедуры все допустимые (относительно исходного смешанного графа) сетевые графики.

Поскольку нас интересует оптимальное (по быстродействию) расписание, то среди указанного множества расписаний целесообразно выделить расписание, при котором каждая операция начинает выполнятся в момент времени завершения всех предшествующих ей операций. Тем самым каждому бесконечному графу, порождаемому рассматриваемым смешанным графом, будет соответствовать одно вполне определенное расписание.

На рис. 2 изображены два бесконтурных графа (сетевые графики), порождаемых графом, изображенным на рис. 1, в результате замены всех его ребер дугами. Каждой дуге соответствует длительность выполнения (1 – одно занятие), каждой вершине приписано календарное время начала выполнения соответствующей операции. Сетевые графики дополнены вершиной Z – окончание всех операций.

Согласно сетевому графику первое расписание является более эффективным, чем второе.

Таким образом, задача построения оптимального по быстродействию расписания может быть решена перебором конечного числа возможных вариантов расписаний. Этот перебор определяется числом бесконтурных графов, порождаемых данным смешанным графом.

4. Эвристический подход. Описанный выше метод построения допустимых расписаний включает построение бесконтурного ориентированного графа и последующие вычисление необходимых временных характеристик по полученному сетевому графику.

Конструирование графа осуществляется пошагово и на каждом шаге осуществляется выбор очередной операции из множества возможных претендентов. От того, на сколько правильно на каждом шаге осуществляется этот выбор, зависит качество получаемого в дальнейшем допустимого расписания.

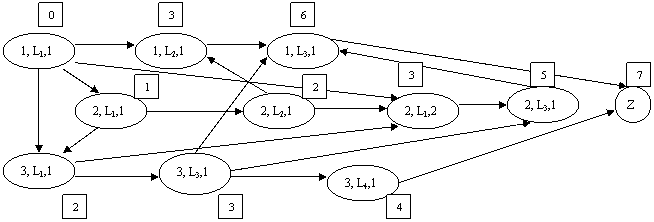
а)

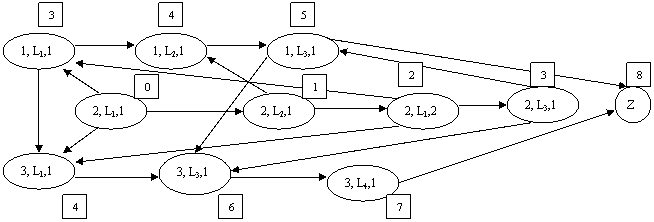
б)

Рис. 2 Бесконтурные графы (сетевые графики)

Поскольку анализ всех возможных последствий выбора той или иной операции практически не реализуем, появляется необходимость принимать решение в условиях относительной неопределенности, на основе анализа ограниченного объема информации, имеющейся к моменту принятия решения. Поэтому представляется целесообразным совместить процессы конструирования сетевого графика и расчеты соответствующих временных характеристик [3].

Выбор операции должен проводиться с учетом имеющейся информации с тем, чтобы обеспечить достаточно высокое качество получаемого расписания. С другой стороны, степень полноты учета этой информации определяет скорость построения отдельного расписания, следовательно, число допустимых расписаний, генерируемых за приемлемый промежуток времени.

Известны генераторы, которые за достаточно большой промежуток времени позволяют построить все допустимые расписания ( Г(R) — генератор с равновероятной выборкой, выбирает любую операцию из множества l возможных на данном шаге претендентов с вероятностью 1/l ); генераторы, исключающие из рассмотрения заведомо неконкурентоспособные расписания ( Г(А) — генератор активных расписаний, который при выборе дает предпочтение операции не изменяющей календарное время начала выполнения других операций, в противном случае также выбирает любую операцию с вероятностью 1/l ).

Наиболее распространены на практике генераторы, использующие разнообразные правила предпочтения (приоритеты). Но они не гарантируют получения оптимального расписания.

В генераторе LRT (longest remaining time) заложено правило быстрее обслужить требование, общая длительность обслуживания которого является наибольшей (преподаватель с наибольшей нагрузкой).

Генераторы FIFO, LIFO (First In— First On, Last In— Last On) используют правило «первый пришел— первый обслуживается» и «последний пришел — последний обслуживается» соответственно, в первом случае выбирается операция с наименьшим календарным временем начала выполнения, во втором— с наибольшим.

Существует также множество видов генераторов, которые используют одновременно несколько даже противоречивых условий с равной вероятностью, например, правила генераторов FIFO и LIFO. Эффективность выбора того или иного генератора определяется временем решения поставленной задачи.

Выводы:

            1. В работе предложены линейная и сетевая модели задачи распределения в теории расписания.

            2. Не зависимо от выбора алгоритма и модели данной задачи, ее решение является трудоемким за счет большого числа входных данных и переменных, и поэтому, обобщая модель задачи распределения, не следует пренебрегать ее частными результатами.

            3. Использование статистического подхода по выявлению эффективного алгоритма решения задачи распределения в теории расписаний требует разработки статистической модели предметной области, основной задачей которой является генерация исходных данных в соответствии с установленными законами распределения случайных величин. Естественно, что множество исходных данных должно быть сформировано в соответствии с требованиями и ограничениями, накладываемыми предметной областью.

            3. Эффективность решения задачи распределения в теории расписания возрастает при комплексном и последовательном использовании рассмотренных алгоритмов.

1.                  Танаев В.С., Сотсков Ю.Н., Струсевич  В.А. Теория расписаний. Многостадийные системы.— М.: Наука, 1989. — 328 с.

2.                  Ху Т. Целочисленное программирование и потоки в сетях.—М.: Мир, 1979.— 519 с.

3.                  Танаев В.С., Гордон В.С., Шафранский Я.Н. Теория расписаний. Одностадийные системы.— М.: Наука, 1984. — 381 с.