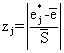УДК 621.3
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА УПРАВЛЕНИЯ КИНЕМАТИЧЕСКОЙ ТОЧНОСТЬЮ ШАРИКО-ВИНТОВЫХ ПЕРЕДАЧ
Вайсман В.А.
Актуальной проблемой современного машиностроения является совершенствование технологии шарико-винтовых передач (ШВП) и расширение ассортимента изделий, где они применяются, что связано с тем, что ШВП организует передачу крутящего момента при помощи подшипников качения. Этот подход является энергетически оправданным, т.к. приводит к экономии затрат. Кроме того, значительное увеличение количества циклов и надежность опредеяют широту применения ШВП – от автомобильных подъемников до атомных электростанций. В последнем случае требования к точности геометрических параметров винта, гайки и шариков весьма высоки, т.к. погрешности изготовления значительно снижают нагрузочную способность, долговечность и надежность работы передачи.
Анализ последних публикаций [1-4] показал, что отечественными учеными недостаточно внимания уделяется проблеме математического моделирования процесса управления точностью изделий станкостроения, как одного из основных свойств, характеризующих их качество. А ведь проблема качества и повышения конкурентоспособности становится ключевой для предприятий Украины, способствуя очевидному росту интереса к стратегическим вопросам бизнеса и к проблеме качества, а также к подходам и методам их решения.
Одной из нерешенных задач в этой области является математическое моделирование процесса управления кинематической точностью ШВП. При этом необходимо учитывать, что неточности, вызываемые случайными факторами, оказывают существенное влияние на кинематику передачи, что приводит к снижению ее эффективности в составе соответствующих механизмов и машин.
Изложение исследований. Для проведения статистических расчетов кинематической точности шариковых винтовых передач (ШВП) необходимо определить вероятностные характеристики случайной функции, которая в каждом опыте, сводящемся к случайному выбору винта из имеющейся совокупности винтов, принимает конкретный вид. При этом областью задания этой функции Е = Е(s) следует считать диапазон изменения s, соответствующий измеряемой длине резьбы винта.
При расчете параметров кинематической точности ШВП в качестве исходных данных принимаются наборы экспериментально полученных точек Аi(γi, еi), i = 1, 2, …, n (каждой ШВП соответствует свой набор) в декартовой системе координат Оγе, по оси абсцисс которой откладывается угол γ поворота винта, а по оси ординат – отклонение е от действительного перемещения точки касания шарика с канавкой от номинального.
Перейдем от аргумента γ к аргументу s – расстоянию указанной точки касания от ее начального положения, соответствующего γ=0, отсчитываемому по теоретической траектории этой точки, представляющей собой винтовую линию. Если R и h – соответственно, радиус и шаг этой линии, то ее параметрические уравнения в соответствующей декартовой системе координат будут следующими:
x = R Cos γ, y = R Sin γ, z = ![]() [1].
[1].
Поэтому 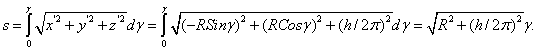
![]() - формула перехода от γ к s. Будем считать, что в дальнейшем, согласно этой формуле, величина γ заменена на s.
- формула перехода от γ к s. Будем считать, что в дальнейшем, согласно этой формуле, величина γ заменена на s.
Теоретически, при неограниченном увеличении n, набор точек Аi(γi, еi), i = 1, 2, …, n трансформируется в некоторую кривую, представляющую собой для данной ШВП графическую зависимость е от s. Соответствующую этой кривой непрерывную функцию е = е(s) будем считать реализацией случайной функции неслучайного аргумента Е = Е(s), представляющей собой зависимость случайного отклонения Е действительного перемещения от номинального (для совокупности всех винтов данного типоразмера) от s .
Таким образом, Е = Е(s) – случайная функция, которая в каждом опыте, сводящемся к случайному выбору винта из имеющейся совокупности винтов, принимает конкретный вид е = е(s) зависимости е от s для этого винта. При этом областью задания функции Е = Е(s) будем считать диапазон изменения s, соответствующий измеряемой длине резьбы винта. Иными словами, каждый конкретный винт отождествляется с одной из реализаций е = е(s) случайной функции Е = Е(s).
Пусть Е – случайная величина, являющаяся сечением случайной функции Е = Е(s) при произвольном фиксированном значении аргумента s = s0. Необходимо выяснить, подчиняется ли Е нормальному закону распределения. Известно несколько способов проверки этой гипотезы [5]. Однако, как показывает практический опыт применения этих способов, оптимально использовать одновременно два из них: по размаху варьирования и по c2-критерию.
Первый из них весьма прост, служит для быстрой проверки и при положительном результате ориентирует на применение второго способа – для точной проверки нормальности распределения. Первый способ применим для случая 3 < n < 1000. Его суть заключается в следующем: вычисляется размах варьирования R = emax – emin, где emax = max {ei}, i = 1, 2, …, n; emin = min {ei}, i = 1, 2, …, n; подсчитывается отношение R/S, где 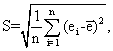 ei – экспериментально полученные значения случайной величины Е = Е(s0) и
ei – экспериментально полученные значения случайной величины Е = Е(s0) и ![]() - среднее этих значений, и это значение сопоставляется с критическими верхней и нижней его границами, приведенными в табл. 1 [5].
- среднее этих значений, и это значение сопоставляется с критическими верхней и нижней его границами, приведенными в табл. 1 [5].
Таблица 1
|
Объем выборки |
Нижние границы |
Верхние границы |
|||||||||||
|
|
Вероятность ошибки |
||||||||||||
|
|
0,000 |
0,005 |
0,010 |
0,025 |
0,050 |
0,100 |
0,100 |
0,050 |
0,025 |
0,010 |
0,005 |
0,000 |
|
|
3 |
1,732 |
1,735 |
1,737 |
1,745 |
1,758 |
1,782 |
1,997 |
1,999 |
2,000 |
2,000 |
2,000 |
2,000 |
|
|
4 |
1,731 |
1,830 |
1,870 |
1,930 |
1,980 |
2,040 |
2,409 |
2,429 |
2,439 |
2,415 |
2,447 |
2,449 |
|
|
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
|
|
1000 |
1,999 |
5,500 |
5,570 |
5,680 |
5,790 |
5,920 |
7,110 |
7,330 |
7,540 |
7,800 |
7,990 |
44,70 |
|
Если R/S оказывается меньше нижней или больше верхней границы, то нормального распределения нет. Если же R/S оказывается в пределах между нижней и верхней границами, то можно рассчитывать, что Е приближенно подчиняется нормальному закону распределения. Следовательно, можно перейти к применению методики по c2-критерию. Ее суть состоит в следующем. Производится группирование экспериментально полученных чисел:
ei, i = 1, 2, …, n. (1)
Для этого промежуток <emin, emax>, содержащий эти числа, разбивается на k интервалов одинаковой длины Dе и подсчитывается количество элементов выборки (1), попавших в каждый из указанных интервалов nj, j = 1, 2, …, k. Значениям е, находящимся в одном и том же j-ом интервале, приписывается значение ![]() , которое соответствует середине указанного интервала (при этом наблюдения, попадающие на границу (j – 1)-го и j-го интервалов, следует относить к интервалу с номером 1).
, которое соответствует середине указанного интервала (при этом наблюдения, попадающие на границу (j – 1)-го и j-го интервалов, следует относить к интервалу с номером 1).
После группирования данные удобно представлять таблицей следующего вида:
Таблица 2
Номера интервалов |
Середины интервалов |
Частоты интервалов nj |
1 |
|
n1 |
2 |
|
n2 |
¼ |
¼ |
¼ |
k |
|
nk |
Примечание: nj – абсолютная частота для j-го интервала, т.е. количество элементов выборки (1), попавших в этот интервал.
Предварительное количество kпр интервалов группирования рекомендуется находить из полуэмпирического соотношения kпр = 1 + 3,32 lg n с округлением в сторону ближайшего целого числа.
После этого определяется длина интервалов ![]() Середина промежутка <emin, emax>
Середина промежутка <emin, emax> ![]() принимается в качестве центра некоторого интервала, после чего легко можно найти границы и окончательное количество k указанных интервалов так, чтобы в совокупности они перекрывали промежуток <emin, emax>. После этого заполняется табл.2, являющаяся фрагментом таблицы 3.
принимается в качестве центра некоторого интервала, после чего легко можно найти границы и окончательное количество k указанных интервалов так, чтобы в совокупности они перекрывали промежуток <emin, emax>. После этого заполняется табл.2, являющаяся фрагментом таблицы 3.
В таблице 3
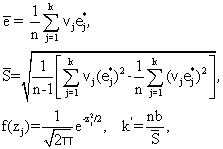
где b – длина интервалов; ![]() - ожидаемая по стандартному нормальному распределению (т.е. по распределению с плотностью вероятности
- ожидаемая по стандартному нормальному распределению (т.е. по распределению с плотностью вероятности ![]() ) частота для j-го интервала.
) частота для j-го интервала.
Расчетное значение c2 для всех интервалов вычисляется по формуле
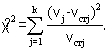
Таблица 3
|
Номера Интервалов |
Середины интервалов ej*
|
Частоты интервалов nj
|
|
nj |
nj |
|
|
f(zj) |
nстj = k’ f(zj) |
nj - nстj |
(nj - nстj )2 |
(nj - nстj )2/ nстj |
|
1 |
|
n1 |
( |
n1 |
n1( |
|
z1 |
f(z1) |
nст1 |
n1-nст1 |
(n1-nст1)2 |
|
|
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
¼ |
|
k |
|
nk |
( |
nk |
nk( |
|
zk |
f(zk) |
nстk |
nk-nстk |
(nk-nстk)2 |
|
Это значение сравнивается с табличным c2 (n, р%) при заданном уровне значимости р% (например, 10%-ном) и числе степеней свободы n = k – 1 – 2 ( т.к. оцениваются два параметра ![]() ). В случае, если
). В случае, если ![]() £ c2 (n, р%), то гипотеза о нормальности закона распределения случайной функции Е = Е(s) принимается, в противном же случае – отвергается.
£ c2 (n, р%), то гипотеза о нормальности закона распределения случайной функции Е = Е(s) принимается, в противном же случае – отвергается.
Вывод. Положительный результат такой проверки существенно упрощает исследование кинематической точности винтов ШВП. Если будет установлено, что Е(s) обладает этими свойствами, то в процессе последующего производства винтов данного типоразмера можно будет подвергать изучению не всю серию винтов, а всего лишь несколько (либо даже один из этих винтов), что, разумеется существенно сократит затраты времени на контроль точности и повысит эффективность производства.
In the article the decision of task of statistical research of kinematics exactness of ball-shaped helical gears is expounded, that allows to handle the process of rise of their quality, to minimize the expenditures of time on the control of exactness of wares and promote efficiency of the ball-shaped helical gears production.
1. Емельянов И.Я., Воскобойников В.В., Масленок Б.А. Основы проектирования механизмов управления ядерных реакторов.– М.: Атомиздат, 1978.– С.223.
2. Рудя Н., Сизонтов В. Горизонты станкостроения // Деньги и технологии.— 2003.— №9.— С. 24-28.
3. Грузнов И.И. Механизмы интенсификации обновления продукции (теоретические и прикладные основы).– Одесса: ОНПУ, 2004.– 288 с.
4. Осипов В.Н., Диленко В.А., Стрелец А.А. Оценка конкурентоспособности продукции производственного назначения.– Одесса: ИПРРЭИ НАН Украины, 2004.– 152 с.
5. Львовский Е.Н. Статистические методы построения эмпирических формул. – М.: Высшая школа, 1982. – 224 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.