УДК 517.977
МОДЕЛІ І МЕТОДИ ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ ВИРОБНИЦТВА
Пляшкевич О.М.
Введення. Кожен виробник, приймаючи рішення про витрати і випуск продукції, переслідує ту чи іншу мету. У сучасній економічній теорії затвердився підхід, відповідно до якого виробник прагне приймати такі рішення, що забезпечували б йому одержання максимального прибутку. Однак у виробника можуть бути й інші мети: максимізація обсягу продажів, доходу в розрахунку на одного працівника, мінімізація витрат та ін.
Мета статті. Постановка задачі. Виробництво благ здійснюється за допомогою використання визначених факторів виробництва, відповідно до заданої технології. Нас цікавлять не фізичні характеристики цієї технології, а ті кількісні залежності, що існують між витратами ресурсів і випусками продукції й обумовлені цією технологією. Випускаються виробником блага надалі будемо, як це прийнято в економіці, називати продукцією. Виробник може споживати (використовувати для виробництва) кілька факторів (ресурсів) і випускати кілька видів продукції. Позначимо через хj(j=![]() ) кількість j-го фактора виробництва, використовуваного виробником. Тоді обсяги витрат усіх факторів виробництва, використовуваних виробником, можна представити як вектор х=(х1,х2,...,хn), який має назву вектор витрат факторів чи виробництва виробничих ресурсів. Під простором витрат
) кількість j-го фактора виробництва, використовуваного виробником. Тоді обсяги витрат усіх факторів виробництва, використовуваних виробником, можна представити як вектор х=(х1,х2,...,хn), який має назву вектор витрат факторів чи виробництва виробничих ресурсів. Під простором витрат ![]() будемо розуміти безліч усіляких векторів витрат виробника, що є ненегативним ортантом n-ірного векторного простору Eт, тобто
будемо розуміти безліч усіляких векторів витрат виробника, що є ненегативним ортантом n-ірного векторного простору Eт, тобто
![]() ={х=(х1,х2,...,хn):xj≥0, j=
={х=(х1,х2,...,хn):xj≥0, j=![]() }.
}.
Так як п=2, то ![]() представляє безліч векторів першої чверті площини x10x2 .
представляє безліч векторів першої чверті площини x10x2 .
Простір витрат може являти собою і деяку замкнуту чи відкриту безліч витрат G![]()
![]() . Тут x
. Тут x![]() і x
і x![]() - мінімальні обсяги ресурсів, необхідних для підтримки процесу виробництва в робочому стані, x1max і x2max - максимальні обсяги ресурсів, що маються на ринку ресурсів.
- мінімальні обсяги ресурсів, необхідних для підтримки процесу виробництва в робочому стані, x1max і x2max - максимальні обсяги ресурсів, що маються на ринку ресурсів.
Варто помітити, що, як і у випадку споживача, при моделюванні поводження виробника простір витрат може бути представлене у вигляді безупинної безлічі, дискретної чи безлічі дискретно-безупинної безлічі. Але ми надалі будемо розглядати тільки безупинний простір факторів виробництва, тобто будемо припускати, що усі фактори виробництва є діленими. Кожному вектору х витрат факторів виробництва відповідають визначені обсяги випуску продукції при даній технології. Позначимо через уi(i=![]() ) обсяг випуску i-го виду продукції, тоді вектор у=(y1,y2,…,ym) являє собою обсяги випуску продукції усіх видів, вироблених виробником при використанні витрат факторів виробництва, заданих вектором х. Вектор у назвемо вектором випуску продукції. Таким чином, вектор витрат х визначає вектор у випуску продукції. Пари векторів (х,у) називають технологічним процесом. Сукупність усіляких технологічних процесів (х,у) називають технологічною безліччю виробника, чи безліччю виробничих можливостей. У структурі технологічної безлічі відбиваються особливості технології, так що вивчення технології виробника зводиться до вивчення його технологічної безлічі. Виробника, мабуть, повинні цікавити найбільш ощадливі перетворення виробничих ресурсів у продукти. Технологічний процес (х*,у*) називається ефективним чи оптимальної по Парето, якщо не існує іншого процесу виробника, більш ефективного, чим (х*,у*). Природно, що виробника повинні цікавити тільки ефективні технологічні процеси. Таким чином, існує визначена залежність між використовуваними обсягами факторів виробництва і максимальним рівнем виробництва, якого вони дозволяють досягти.
) обсяг випуску i-го виду продукції, тоді вектор у=(y1,y2,…,ym) являє собою обсяги випуску продукції усіх видів, вироблених виробником при використанні витрат факторів виробництва, заданих вектором х. Вектор у назвемо вектором випуску продукції. Таким чином, вектор витрат х визначає вектор у випуску продукції. Пари векторів (х,у) називають технологічним процесом. Сукупність усіляких технологічних процесів (х,у) називають технологічною безліччю виробника, чи безліччю виробничих можливостей. У структурі технологічної безлічі відбиваються особливості технології, так що вивчення технології виробника зводиться до вивчення його технологічної безлічі. Виробника, мабуть, повинні цікавити найбільш ощадливі перетворення виробничих ресурсів у продукти. Технологічний процес (х*,у*) називається ефективним чи оптимальної по Парето, якщо не існує іншого процесу виробника, більш ефективного, чим (х*,у*). Природно, що виробника повинні цікавити тільки ефективні технологічні процеси. Таким чином, існує визначена залежність між використовуваними обсягами факторів виробництва і максимальним рівнем виробництва, якого вони дозволяють досягти.
Розглянемо найбільш простий випадок. Нехай виробник випускає тільки один вид продукції, що забезпечується одним єдиним фактором виробництва, наприклад працею. Тоді використання праці в обсязі х* дозволяє випустити максимальний обсяг продукції y* чи будь-який інший обсяг продукції z, менший, чим у*. Тоді процес (x*,y*) буде ефективним, а всі інші процеси (x*,z), де 0≤z<у*, будуть неефективними.
Пари векторів (х,у), що задає технологічний процес, можна розглядати як вектор простору Еn+m, що називається вектором витрат - випуску виробника. Тоді технологічна безліч є безліч усіляких векторів витрат-випусків у просторі En+т. Звичайно приймається додаткова гіпотеза про те, що технологічна безліч опукла. Розглянемо такі технологічні процеси, у кожнім з який виготовляється тільки один продукт. Такі процеси назвемо однопродуктовими. Нехай при виготовленні однієї одиниці продукції ресурс j-го виду використовується в кількості аj. Тоді вектор витрат на одиницю продукції а=(а1,a2 ...,an)T.
Якщо випуск продукції складає y одиниць, то тоді вектор витрат ресурсів х=уа.
Нехай тепер той самий продукт виробляється декількома (г) технологічними процесами, причому кожен процес при визначеному сполученні ресурсів забезпечує випуск однієї одиниці продукції. Ці процеси задаються векторами витрат
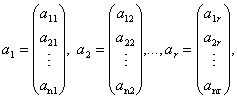
простору Е![]() Якщо y1,у2,...,уr - кількість продукції, що випускається відповідно 1,2,...r процесами, тоді загальний випуск продукції y=y1+у2+……+yr, а вектор витрат ресурсів х=а1у1+а2y2+...+аnyn. Тоді пари
Якщо y1,у2,...,уr - кількість продукції, що випускається відповідно 1,2,...r процесами, тоді загальний випуск продукції y=y1+у2+……+yr, а вектор витрат ресурсів х=а1у1+а2y2+...+аnyn. Тоді пари
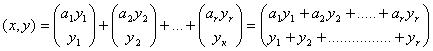
при y1≥0, у2≥0,...,уr≥0 задають технологічну безліч.
Якщо кожен вид затрачуваних ресурсів обмежений (хj≤bj; j=![]() ), тоді можна сформулювати наступну задачу максимізувати загальний випуск продукту при обмежених ресурсах, тобто
), тоді можна сформулювати наступну задачу максимізувати загальний випуск продукту при обмежених ресурсах, тобто
мах у=y1+y2+…....+yr
за умови
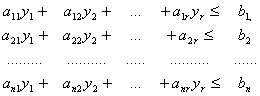
де y1≥0, y2≥0,…yr≥0.
Рішення цієї задачі і виявить ті процеси, які варто використовувати у виробництві даного виду продукції в цій ситуації, тобто це ті процеси, вектори витрат яких ввійдуть в оптимальний базис.
Виробник, як було сказано, намагається домогтися, щоб використовувані процеси були ефективними, і, таким чином, інтерес представляє не вся технологічна безліч, а його границя. Отже, досить розглядати лише функцію, що задає границю технологічної безлічі. Така функція і називається виробничою. Аналогом їй, у теорії автоматичного керування, є передаточні функції. Історично уточнення понять, що відносяться до виробничих функцій, відбувалося на економічній основі, що, можливо, порозумівається наступними причинами. По-перше, виробничі функції самі по собі мають значення для розробки програм економічного розвитку і для визначення межі збільшення зробленого продукту при даних вихідних ресурсах. По-друге, розміри коефіцієнтів виробничих витрат служать базою при визначенні оптимальної структури міжнародної чи міжрегіональної торгівлі. По-третє, це поняття лежить в основі деяких теорій функціонального розподілу доходу. Умови, при яких загальний випуск продукції може бути віднесений за рахунок дії факторів, що брали участь у його створенні, залежать від характеру виробничої функції. По-четверте, виробнича функція забезпечує половину інформації загального характеру, необхідної при визначенні ступеня використання ресурсів і структури випуску, при наявності яких досягається максимум прибутків.
У загальному виді цю функцію можна записати як рівняння з однієї перемінної, що характеризують витрати, можуть використовуватися для виявлення деяких властивостей виробничих функцій і відповідних додаткових продуктів. Ті ж самі властивості звичайно мають місце і при n перемінних. Однак у цьому випадку випуск при використанні тільки одного фактора ніколи не перевищує нуля.
Відповідно виробничу функцію варто представити як
|
Y = f (X1,X2,…Xn) |
(1) |
де Y - випуск,
Xi, - витрати ресурсу.
Загалом, при наявності виробничої функції можна визначити наступні величини, що мають безпосереднє значення для економіки:
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Приведені вираження, що базуються на виробничій функції, дозволяють одержати дані, необхідні для економічного аналізу. Бажано одержати зазначені характеристики для різних видів функцій. Розглянемо їх один по одному: рівняння (2) являє собою рівняння додаткового продукту в натуральному вираженні для i-го ресурсу; рівняння (3) - рівняння граничних норм заменяемості i-го і j-го ресурсів; (4) - рівняння ізоквант; (5) - рівняння ізокліналєй; (6) - рівняння розмежувальних ліній. Якщо вираження, представлене рівнянням (3), підставити в рівняння (5) і (6), то стане очевидним, що кожна з розглянутих величин, установлювана для одного ресурсу, залежить від усього набору ресурсів, що можуть бути використані в даному виробничому процесі.
Звичайно, можна прийняти, що визначені види витрат залишаються постійними в той час, як інші змінюються. Однак визначені чи ресурси категорії витрат є екзогенними в тім змісті, що «вони є результатом дії зовнішніх сил» і не піддаються контролю з боку обличчя, що приймає рішення, чи з боку дослідника. Тому, коли можна контролювати величину лише ресурсів X1, Х2, ... Xg, тоді випадковий чи вплив збурювання асоціюється з перемінними Хg+1,Хg+2,…,Xn
Функція Кобба-Дугласа. чи статична функція, звичайно застосовується у виді
|
Y=aXb, |
(7) |
де Х - перемінний ресурс, представлений у якому-небудь вимірі,
Y- випуск продукції,
а - постійна
b - коефіцієнт трансформації величини X.
Функція допускає постійний, зростаючий або додатковий продукт, що знижується. Вона не допускає, щоб крива витрат - випуску охоплювала всі три випадки одночасно. Очікується, що при постійному рівні усіх витрат, крім тих, котрі враховуються функцією, додатковий продукт повинний падати. Рівняння додаткового продукту має вид
|
|
(8) |
Воно показує, що якщо b = 1, тоді додатковий продукт, а також середній продукт, будуть постійно рівні а. Коли b>1, величина додаткових продуктів буде виростати в міру збільшення Х в залежності від величини b. Наприклад, якщо b=2, додаткові продукти складають bа, 2bа, 3bа і 4bа, причому значення Х відповідно рівні 1, 2, 3, 4. Якщо b < 1, то величина додаткових продуктів буде падати в міру збільшення X, оскільки Xb<X.
Цю функцію з визначеними математичними властивостями не можна задовільно використовувати там, де дані охоплюють як збільшуємий, так і падаючий додатковий продукт. Цю функцію не можна задовільно використовувати й у тому випадку, коли дані допускають одержання як позитивних, так і негативних додаткових продуктів. Ступінь зниження випуску додаткового продукту скорочується з збільшенням величини витрат.
Висновки. Дослідники протягом тривалого часу вели дослідження, одержуючи нові зведення про властивості виробничих функцій.. Звичайне проведення досліджень планувалося на основі явища дискретності, тобто застосовувалися два чи кілька технологічних способів виробництва для визначення крапкових оцінок виходу продукції. У деяких випадках, хоча це і був побічний результат, отриманих даних було досить для висновку простих рівнянь чи регресії кривих, що показують залежність випуску від витрат (залежність вхід-вихід). Виходячи з цих розходжень може бути розрахована відносна прибутковість декількох технологічних чи способів видів витрат. Однак у загальному було неможливо застосувати точні економічні принципи для визначення найбільш прибуткового рівня витрат і чи випуску для визначення найбільш вигідної комбінації витрат для одержання обумовленої кількості продукції.
The purposes of the manufacturer are formulated at acceptance of the administrative decisions. The technique of the decision of a task is offered which provides of volume of sales, income in account on one worker, minimization of costs etc. the Decision of a task is carried out with the help of use of the certain factors of manufacture, according to the given technology.
1. Кочура Е.В. Экономическая кибернетика. - Днепропетровск: ДУЭП, 2002. – 187с.
2. Марасанов В.В. Элементы теории управленческих решений. – Херсон: Колос, 2002. – 72с.
3. Марасанов В.В., Пляшкевич О.М.Основы теории проектирования и оптимизации макроэкономических систем. – Херсон: Айлант. – 2003. – 140с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Экономика научно-технического прогресса
Портянко Т. М. Формування інтегрованої моделі системи менеджменту якості на підприємствах фармацевтичної промисловостіБойченко О.В., Яценко Л.Ф., Яловенко Ю.В. Информационно-аналитическая система мониторинга хозяйственной деятельности предприятия
Крючковский В.В., Бабичев С.А., Шарко А.В. Экспертная система оценки кредитоспособности банковских клиентов на основе методов нечеткой логики и сети Байеса
Власенко Н.А. Роль інноваційних технологій для підвищення конкурентоспроможності консервних підприємств
Прохоренко Д.В. Определение структуры и свойств организационного механизма управления промышленным производством
Данилец Е.В. Имитационное моделирование систем управления качеством в экономике
Ходаков В.Е., Чёрный С.Г., Мартыновец С.Н. Формирование экспертных оценок при решении задач размещения производств
Рогальский Ф.Б. Информационная поддержка принятия решений при управлении социотехническими системами.
Крючковський В.В. Прийняття рішень при бюджетному інвестустуванні на основі моделі аналізу вигід і витрат
Пляшкевич О.М., Забитовська О.І. Моделі інформаційних технологій оптимізації поведінки виробника
Шеховцов А.В., Славич В.П., Крючковский В.В. Когнитивный анализ социально-экономических показателей.
Соколова Н.А., Петров К.Э., Ходаков В.Е. Необходимые условия развития объектов хозяйственной деятельности
Власенко Н.А. Ринок соків в Україні та одна з альтернатив підвищення конкурентоспроможності продукції
Тодорцев Ю.К., Бундюк А.М., Іщенко К.А. Реінжиніринг бізнес-процесів та ефективність бізнесу
Лошак Т.В., Ладанюк А.П. Ефективність реінжинірингу бізнес-процесів харчових виробництв.
Купцова Е.Е., Деменский А.Н., Быря А.П. Научно-технический прогресс и возобновляемые источники энергии.
Рогальська Н.Г. Моделі оптимізації фінансової діяльності великих економічних систем з використанням кореляційного аналізу
Крючковский Д.А., Полетаева А.Н. Динамическая система торговых отношений в интернете
Соколова Н.А., Ходаков Д.В., Ходаков В.Е. Организация координации в системах управления объектами хозяйственной деятельности.
Пляшкевич О.М. Виробничі функції в аналізі технологій підприємств
Пляшкевич О.М. Інформаційна модель оптимальної поведінки виробника в умовах конкуренції
Бундюк А.Н. Анализ бизнес – процессов теплогенерирующего предприятия
Скороход Е. Н. Модель поддержки принятия решений при управлении рыбовод-ным предприятием
Бабенко Н.И., Крючковский Д.А., Маломуж Т.В. Методы снижения влияния факторов субъективности и неопределенности в системах поддержки принятия решений.