УДК 622.673.8

СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ОКОМКОВАНИЯ ЖЕЛЕЗОРУДНОГО КОНЦЕНТРАТА В УСЛОВИЯХ ЦГОКА

Чернецкая И.Е., Исаев Е.А., Лебеденко Ю.А.

Введение

Одним из важнейших технологических процессов на Криворожском Центральном горнообогатительном комбинате является процесс грануляции железорудных окатышей, осуществляемый на промышленном окомкователе. Сложность промышленного оборудования и невозможность проведения экспериментальных исследований для определения требуемых параметров технологического процесса требует разработки эффективных математических моделей и методик определения оптимальных параметров.

Анализ последних исследований и публикаций

Математическое описание процесса грануля­ции на промышленном окомкователе с учетом физико-химического сос­тава шихт в условиях Криворожского Центрального горнообогатительного комбината имеет вид [1]:

                                                                                                                    (1)

                                                                           (2)

где          Х₁ - производительность окомкователя, т/час;

Х₂ - скорость вращения чаши, об/мин ;

Х₃ - влажность шихты, %;

Х₄ - содержание железа в шихте, %;

Y₁ –разность выходов окатышей кондиционного размера
 (10  20 мм) и крупных кусков ( 20 мм);

 Y_{2 -} прочность окатышей на сбрасывание.

Здесь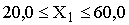

  (3)

Проверка математической модели (1),(2) на промышленном объекте подтвердила адекватность описания процесса окатывания выбранными полиномами и позволяет использовать их для прогнозирования процесса окомкования. Из рассмотрения уравнений регрессии процесса окомкования приходим к заклю­чению, что показатель качества Y₁, геометрически представляет собой гиперповерхность (холм), обладающий свойством унимодальности.

Целью данной статьи является разработка методики определения оптимальных параметров окомкователя, доставляющих максимум некоторому показателю качества. В качестве показателя качества выбрана разность выходов окатышей кондиционного размера и крупных кусков.

Основной материал исследования

Для нахож­дения оптимальных значений параметров, при которых  (где Y₁- показатель качества), использован метод статистического градиента.

Суть метода заключается в том, что отыскивается максимально возможное значении показателя качества Y₁, путем соответ­ствующего выбора векторов контролируемых параметров Х₁, Х₂, X₃, X₄, удовлетворяющих наложенным ограничениям (3).

Для отыскания максимума Y₁ (1) использовалась следующая методика:

I. При имеющихся n переменных параметрах определяем единичные случайные векторы, равномерно распределенные по всем направлениям пространства параметров (по выражениям (1) и (2)):

а)        находим равномерно распределенную случайную величину  в интервале 0,1 по координате Х_1-1;

б)       находим следующую равномерно распределенную в интервале 0,1 случайную величину  по координате Х_1-2 ;

в)        проверка неравенства  (4)

г) если неравенство (4) имеет место, то имеем единичный вектор, показывающий направление к области оптимума, если нет - то находим следующую равномерно распределенную случайную величину  по координате Х_1-3 и т.д.

2. Определив m единичных случайных векторов, найдем векторную сумму, применив выражение:

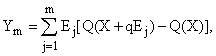
или в скалярной форме

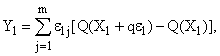                                                    (5)

и т.д. для n параметров,

где          Y_m – векторная сумма, являющаяся статической оценкой градиентного направления;

E_j – вектор пробного шага, движение по которому приводит к увеличению функции качества;

Q (X_j) – наибольшее значение функции качества за i предыдущих шагов. Направление рабочего шага в скалярной форме

где          a – постоянный коэффициент;

Y₁ – значение функции качества в точке max;

Y_m – максимальное значение функции качества (Y_m=100%).

По приведенной методике была разработана программа для ЭЦВМ по нахождении максимального выхода Y₁=Y_1max Результаты вычислений следующие:

Y₁ = 97,9736 %; X₁ = 24,9781 т/час; X₂ = 11,4897 об/мин;

X₃ = 8,67649 %; X₄ = 59,8509 %; Y₂ = 12,9374.

Таким образом, наибольшую разность выходов годных окатышей и крупных кусков можно получить до 98,0%; при этом влажность шихты должна быть около 8,7% и содержание железа 59,8%. Полученные результаты подтверждают данные о процессе окомкования на чашевых грануляторах в условиях КЦГОКа [1] и, кроме того уравнения (1) и (2) адекватны процессу. Поэтому эти выражения были использованы при построении алгоритма с целью автоматизации ча­шевых окомкователей.

Построение алгоритма оптимальности окомкования производили по выражениям (1) и (2). Величины X₁, Х₃, Х₄, заданы в интервалах соответственно (20,0… 60,0), (8,3… 9,6), (54…62).

Использовали следующую методику:

I.                   Для равномерного просмотра интервалов задания величин, Х₁, Х₃ и Х₄ генерировали случайное число из интервала, затем пересчитывали в заданные интервалы (а, b) по выражению:

                                                                        (6)

2. Высчитывали значения Y₁ и Y₂ для исходных точек X_1i, Х_3i и Х_4i.

3.          Если значения (X_1i, Х_3i и Х_4i) не удовлетворяли условию *⁾ Y₂(X_1i, Х_3i и Х_4i)  генерировали новую тройку чисел X_1j, Х_3j и Х_4j.

4.          Если условие *⁾ удовлетворялось, то высчитывали такое значение,  для которого выполняется

Y₁=Y_1max( X₄, X₁, X₂)                                                           (7)

5. В результате проведенных операций получим таблицу

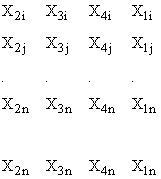
Обработали эту таблицу по методу наименьших квадратов и определили коэффициенты полинома

В результате расчетов получено адекватное уравнение регрессии, которое отвечает условиям оптимальности процесса окомкования:

                                                                                                             (8)

где                                         Y1 = Y1max

                               Y2  (10,22)

                               т/час;

                               %;

                               %.

Анализируя (8) можно сказать следующее. Для оптимизации получения окатышей при увеличении влажности поступающей на окомкование шихты (фактор Х₃ ) необходимо снижать скорость вращения чаши, или увеличивать производительность гранулятора (фактор Х₁). С ростом содержания добавок (уменьшение содержания железа) условия окомкования улучшаются и, для получения гранул заданного размера, при прочих оптимальных условиях необходимо снижать скорость вращения чаши. Из (8) видно, что производительность по исходному питанию (фактор Х₁) оказывает значительное влияние на положение статической характеристики объекта, поэтому при разработке системы автоматического регулирования работой окомкователя необходима стабилизация этого параметра на оптимальном уровне. То есть, выражение (8) является алгоритмом оптимального ведения процесса окомкования, так как оно позволяет подобрать такое значение скорости вращения чаши (Х₂), которое дает максимально возможный выход окатышей при данной входной ситуации, определяемой факторами Х₁, Х₃, Х₄. Для проверки выше приведенного алгоритма были сняты зависимости изменения параметров шихты и продуктов окомкования во времени при настройке процесса на максимальный выход окатышей.

Результаты исследований подтверждают, что при полученном алгоритме оптимальности управления действительно обеспечивается скорость вращения чаши, позволяющая поддерживать выходную величину в зоне оптимума (Y₁ = Y_1max).

Алгоритм оптимальности процесса окатывания (8) был реализован на аналоговой вычислительной машине типа АВК-31, при этом выражение (8) в форме, удобной для моделирования имеет вид:

                                                         (9)

Здесь                                   

 (в);

 (в);

 (в).

Алгоритм оптимальности процесса (8) является астатической характеристикой чашевого окомкователя, т.е. представляет геометрическое место точек, которое определяет вершину "холма" показателя качества при разных значениях возмущающих воздействий: влажности и содержания железа в шихте. Выражение (8) может быть записано  при

В этом случае задача оптимизации окомкования может быть сведена к задаче поддержания скорости вращения чаши, которая соответствует выходной величине устройства, реа­лизующего выше приведенный алгоритм. Другими словами, автоматическое управление окомкованием осуществляется с использованием следящей системы, на вход которой поступает случайное возмущение (оптимальное значение скорости вращения чаши).

Расчет следящей системы сводится к определению передаточной функции объекта, выбору и расчету настроек регулятора, которые бы удовлетворяли определенным показателям качества. При расчете следящей системы учет динамических свойств объекта сводится к учету постоянных времени, определяемых по кривой разгона или расчетным путем.

Для определения постоянных времени цепи возбуждения Т_в, электромеханической постоянной Т_м произведен расчет параметров привода окомкователя .В результате расчетов определили передаточную функцию объекта по управляющему воздействию.

или, с учетом численных значений параметров

                                         (10)

поскольку в нашем случае желательно иметь более точное воспроизведение заданной скорости вращения чаши, то в системе предпочтительно использовать ПИ-регулятор.

После преобразований (10) и подстанов­ке  имеем АФХ объекта:

Амплитудно-частотная характеристика объекта:

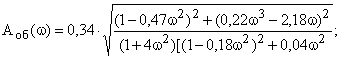                            (11)

 Фазо-частотная характеристика объекта:

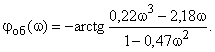                                                     (12)

 По этим выражениям, задаваясь  от 0 до 5 рад/сек, была построена АФХ объекта .

Для определения оптимальных значений коэффициента передачи регулятора (К_ропт) и времени изодрома (T_uопт ) построена АФХ разомкнутой системы при К_р=I и Т_р=1,2,5,10 сек. В результате расчетов установлено, что оптимальные К_ропт и T_uопт равны, соответственно 5,0 в×сек и 1,5 сек. При этих данных па­раметров обеспечивается минимальное значение квадратичного интегрального критерия качества при М=1,3. Запас устойчивости системы по модулю и фазе определялся с использованием частотного критерия Найквиста-Михайлова. Первоначально рассчитывалась АФХ регулятора

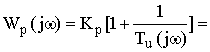
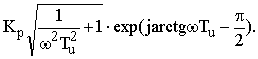                                (13)

Подставляя К_р=5,0; Т_u=1,5 сек и =0…5 рад/сек в выражение (13) имеем АФХ регулятора. На рис.1 представлена АФХ разомкнутой системы.

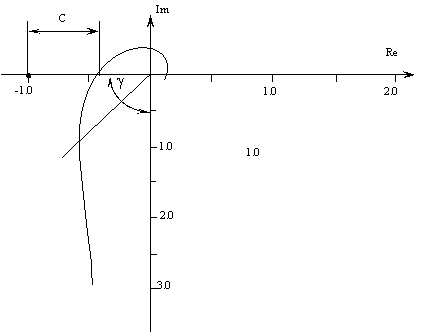
Рис.1.Амплитудно-фазовая характеристика разомкнутой системы.

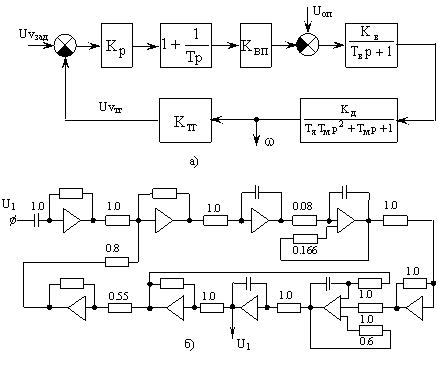
Рис. 2 а – структурная схема САУ;

б – структурная схема модели САУ.

Согласно рисунку 1 запас устойчивости по модулю С=0,5 и по фазе 45°, Таким образом, система автоматического регулирования скорости окомкователя с ПИ-регулятором (Кр=5 в×сек и Т_u=1,5 сек) устойчива и имеет значительный запас устойчивости как по модулю, так и по фазе. Структурная схема САУ представлена на рис.2 (а). Для окончательной оценки правильности расчета настроек регулятора строили переход­ный процесс при возмущении со стороны регулирующего органа. В этом случае АФХ замкнутой системы имеет вид:

 По вещественной частотной характеристике построен переходный процесс и представлен на рис.3 (кривая I). Сравнение переходных процессов, полученных расчетом и моделированием (кривых 1 и 2 соответственно) подтверждает правильность проведенных расчетов настроек регулятора. Итак_, основные параметры переходного процесса:

величина перерегулирования  статическая ошибка               

время регулирования  сек.

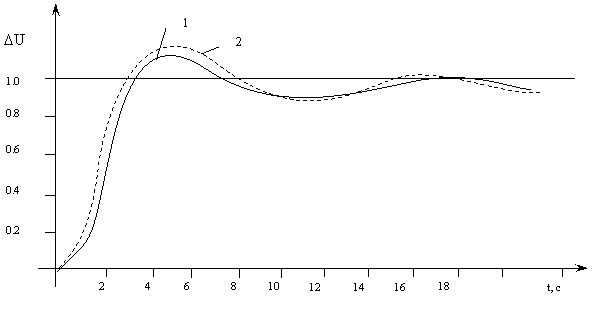
Рис. 3 Переходный процесс замкнутой САУ.

Вещественная частотная характеристика (ВЧХ) замкнутой системы определялась из выражения:

.

Исходные параметры процесса окомкования (влажность шихты W и содержание в ней железа Fe) представляют собой случайные величины, т.е. необходимая скорость вращения чаши () по выражению (8) также представляет собой случайную величину. Прохождение случайных сигналов через САР предъявляет определенные требования к последним. Главным из этих требований является то, что система управления на выходе должна воспроизводить входной сигнал с возможно большей точностью. Это требование особенно жестко, если изменение случайного сигнала на входе соизмеримо по времени с длительностью переходного процесса в системе управления. В этом случае в систему должны быть введены корректирующие звенья для уменьшения среднеквадратичной ошибки выхода при воспроизведении входного сигнала.

Для определения точности воспроизведения входного сигнала на выходе системы снимались зависимости влажности W и содержания железа Fe в шихте в течении длительного промежутка времени. При этом, как оказалось, параметры W и Fe значимо изменяются за время не менее 60  80 сек, т.е. время переходного процесса в системе t_рег в 46 раз меньше, чем существенные изменения параметров физико-химического состава шихты. Значения W и Fe вводились в устройство реализации алгоритма (8) на выходе которого получали кривую оптимальной скорости вращения чаши. Эти данные вводились в модель следящей системы (рис.2,б), на выходе которой снимали напряжение, пропорциональ­ное действительной скорости вращения чаши. Сопоставление кривых оптимальной скорости вращения чаши и фактического ее значения показывает, что следящая система достаточно хорошо отрабатывает входное воздействие (). Таким образом, динамические характеристики окомкователя в рассматриваемой системе могут не учитываться и объект по принятому каналу управления может быть представлен безинерционным звеном.

Система автоматического управления процессом окомкования с использованием алгоритма проверена в промышленных условиях. В качестве датчика физико-химического состава шихты использовался измеритель влажности. Результаты промышленных испытаний системы подтвердили надежную работу всех узлов системы и показали, что функция качества не выходит из области оптимума, т.е. алгоритм действительно обеспечивает оптимальность процесса окомкования. Использование алгоритма в системе автоматического управления чашевым окомкователем позволило увеличить выход окатышей с одной чаши на 2,5%.

Выводы

Разработанный алгоритм оптимальности процесса окомкования в режиме переката позволяет прогнозировать значение скорости вращение чаши, при которой поддерживается максимальный выход окатышей.

Вместе с тем отметим, что производительность чашевого окомкователя оказалась несколько ниже установленной нормы (Р=30 т/час), что свидетельствует о том, что этот аппарат не представляет собой совершенной кон­струкции для производства окатышей и режим окомкования перекатом целесообразно заменить на режим повышенных динамических нагрузок (ПДН) [2] .

1.                   Исаев Е.А. Алгоритм интенсификации окомкования материалов в чашевом окомкователе – Херсон, 1998. – 9 с. Деп.в УкрНИИ НТИ 30 мая 1999 № 1160УК-99 Деп.

2.                   Исаев Е.А., Чернецкая И.Е. Способ окомкования сыпучих материалов, Патент Российской Федерации на изобретение № 2199596 от 27.02.2003г.