Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 519.95.

ЭНТРОПИЙНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ ГРАВИТАЦИОННЫХ МОДЕЛЕЙ.

Марасанов В.В., Забитовская О.И., Щербина Е.В.

Постановка проблемы. Построение баз знаний экспертных систем прогноза спроса является актуальной проблемой и ее решения можно обосновать на аналогии между экономическими и физическими системами, которые являются столь глубокими, что были положены в основу исследования экономических систем и сформированы в виде принципов Ле Шателье – Самуэльсона и Карно – Хикса.

Решение поставленной задачи. Экономические системы относятся к классу систем, в которых детерминированный характер наблюдаемых процессов (усредненные характеристики) сочетается с их стохастической природой. Формальная модель этого класса, которую будем называть макросистемой, описывает преобразование случайных межэлементных микровзаимодействий (товарообмена) в некоторый вполне регулярный процесс (спроса на то (те) или иной (иные) виды продукции).

Тем самым в макросистеме выделяются два уровня: микроуровень, где связи между элементами случайны, и макроуровень, на котором связи между параметрами состояния системы, детерминированные в силу законов сохранения и усреднения. Взаимодействия между уровнями или характер преобразования случайных движений элементов макросистемы в регулярный процесс зависит как от конкретного вида системы, так и от тех экономических закономерностей, сочетание которых определяет ее функционирование. К таким системам можно отнести системы обмена или распределения экономических ресурсов. Обычно такой обмен осуществляется между экономическими ячейками и, в зависимости от степени централизации, принятой в данной экономической системе, может быть как чисто стихийным, так и регламентированным (частично или полностью). Однако как бы ни была степень централизации, экономическая система обмена столь сложна, что (случайные) неуправляемые факторы в ней всегда остаются. Тем самым на «микроуровне» экономической системы происходят обменные взаимодействия между ее элементами, которые имеют как случайную, так и детерминированную компоненты. Вес каждой из них зависит то возможностей вмешательства в единичные акты обмена, совершаемые в данной экономической системе. Если такие возможности отсутствуют, то обмен экономическими ресурсами носит чисто случайный характер. Но несмотря на это, система в целом все-таки приобретает «средний ресурс», то есть в ней происходит преобразование случайного процесса обмена в детерминированный процесс, определяющий ее состояния. Таким образом, в системе экономического обмена существует два существенно отличающихся друг от друга уровня: уровень стохастических межэлементных взаимодействий и уровень детерминированных характеристик поведения системы в целом. Это дает основание использовать макросистемную модель для исследования процессов в системах экономического обмена. Математические модели обмена и экономических рынков были построены в работах Парето, Вальраса, Гейла, Леонтьева, фон Неймана, Эджворта и других. Основное внимание в них уделяется изучению условий равновесия. При этом под равновесием понимается такое состояние, для которого функция полезности системы достигается максимума.

Функция полезности является обобщенной характеристикой системы экономического обмена и определяется на множестве частных функций полезности отдельных ее подсистем. Их формирование обычно не представляет большого труда, тогда как установление связи между функциями полезности одельных подсистем и системы в целом оказывается задачей не формальной. Одна из гипотез приводит к функции полезности типа энтропии физической системы.

Закономерности, присущие равновесным состояниям в системах экономического обмена, во многом, аналогичны тем, которые имеют место в термодинамических системах. Они оказались столь глубокими и полезными, что были провозглашены в качестве неких общих для термодинамических систем и систем экономического обмена принципов: Ле Шателье - Самульсона, Карно - Хикса и другие.

Изучение равновесия и динамики систем экономического обмена касается только их макроуровня. Здесь имеется в виду, что модели исследования равновесных состояний, их основные характеристики формулируются через макропеременные системы: цена, процент, капитал и так далее. Характер микровзаимодействия описывается лишь качественно и служит для того, чтобы высказать определенные соображения о свойствах функции полезности системы экономического обмена.[1]

Наряду с существующими аналогиями между процессами, происходящими в термодинамических системах, и процессами экономического обмена последние обладают некоторыми специфическими свойствами, которые будут рассмотрены в дальнейшем и сводятся к тому, что гипотеза о том, что состояние равновесия в микросистеме достигается при максимуме ее энтропии, а с другой – что при этом должны выполнятся некоторые дополнительные условия, учитывающие конечность ресурса. Прежде чем использовать гипотезу об аналогии термодинамических и экономических процессов введем понятие состояния и распределения. Под состоянием системы будем понимать полное описание системы – это описание микросостояния. Под распределением будем понимать описания макросостояния, которое может задаваться в виде матрицы или многомерной функции плотности вероятности. Наша задача, связана с прогнозированием спроса в конечном итоге, сводится к анализу межрегиональных потоков товаров отражающих реализацию этого спроса.

Предположим, что имеется некоторое множество регионов (предприятий, фирм)  обменивающихся экономическими товарами, причем товары разбиты на группы (продукты питания, сырье, энергоносители и так далее). Межрегиональную транспортную сеть можно описать с помощью стоимостей перевозок отдельных продуктов между регионами и сформулировать задачу в виде экономической гравитационной модели. Кроме того, будем предполагать, что имеется всего один тип коммуникаций (например автотранспорт). Пусть -средняя стоимость перевозки единицы продукта типа  из пункта отправления  в пункт назначения ; -средняя стоимость перевозки продукции типа из пункта отправления, находящего в  в пункт назначения, находящегося в  (внутригородские перевозки, -междугородние перевозки). Пусть -полный поток продукта типа  (спрос на продукт  в пункте , удовлетворяемый пунктом ) измеряемый в единицах, принятых для данной группы продуктов.

Тогда  есть полный объем продукта , производимый в регионе .

Аналогично -полный объем продукта , используемый для производства других продуктов или потребления в регионе  (спроса на продукт  в регионе ). Обозначим также через  и  полное производство и потребление (понимая под «потреблением» использование всеми секторами, в том числе и личное потребление) в регионе ;  - полное производство в системе; , так как предполагаем, что система замкнута (тогда  - общее производство продукта , например сбора зерна, а  - общий спрос - общее потребление).

После введенных обозначений для нахождений оптимальных решений введем понятие гравитационной модели, основанной на аналогии пространственных взаимодействий в классической физике.

Будем интерпретировать  как массы (количества продукта  связанные с отправлениями и прибытиями из  в ).Стоимость  можно соотнести с расстоянием. Строго ньютоновское взаимодействие сведем к величине .

 

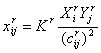                                                     (1)

 

где  - нормирующий множитель, обеспечивающий выполнение равенства

 

       

 

Это означает

 

 

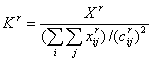
В общем случае взаимодействие может управляться функцией отличной от закона степени (-2), то есть формула (1) может быть записана в виде

 

                                         (2),

 

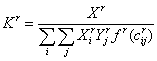где  - убывающая функция , а             (3)

При этом следует иметь в виду, что для разных продуктов эти функции будут иметь различный вид.

Задача оптимизации гравитационной модели может решаться при различной информации о производстве и спроса и может быть четыре возможных случая:

1) существует независимая оценка ;

2) существуют независимые оценки , которые определяют ;

3) существуют независимые оценки спроса , который определяют общий спрос ;

4) существуют независимые оценки , полученные так, что они определяют  по формулам  и .

В уравнениях 2, 3 следует заменить на , а  на  в случаях, когда их независимые оценки отсутствуют. По предположению оценка  существует во всех случаях (например, прогнозируемый сбор зерна), то для оценки  может быть всегда использовано уравнение вида 3. Таким образом уравнения 2 и 3 представляют собой ньютоновскую гравитационную модель для четвертого случая и легко могут быть решены относительно. Для случаев 1 - 3 уравнения 2 и 3 сводятся к квадратному уравнению относительно . [1]

Эти уравнения должны для случая 1 решаться при ограничениях

 

                                                         (4)

 

                                                         (5);

 

-для случая 2 – при ограничениях:

 

                                                             

 

                                                               (6)

 

-для случая 3

                                                               

 

                                                               (7)

 

-для случая 4

 

 

Ограничения 4-7 отвечают условиям производства и полного спроса на произведенную продукцию и соответственно уравнения (2) и (3) никогда не удовлетворяют приведенным условиям непротиворечивости. Поэтому при дальнейшем усовершенствовании модели введем их в качестве ограничений.

Первый случай соответствует модели без ограничений. Заменив  и на  и  можно использовать уравнения (2) и (3).

Второй случай – модель с ограничением на производство. Уравнение (6) выступает в роли ограничения на полное производство в регионе  (например, при заданных технологиях объем выпуска различных видов с/х продукции на ограниченных площадях). Можно найти набор нормирующих множителей, которые заменят единственный множитель , что обеспечит выполнение соотношения (6). Введем множитель  и уравнение 2 перепишем в виде

 

                                              (8),

 

где вместо в уравнении (2) используется, поскольку независимая оценка  во втором случае не предполагается. Тогда по уравнению (6) можно вычислить , если  из (8) подставить в (6). Получим

 

                                             (9)

 

Случай 3 – модель с ограничением на потребление (например, ввиду ограниченного бюджета потребителей). В этом случае ограничением будет уравнение (7). Множитель  заменяется нормирующим множителем,  и стандартные преобразования приводят к следующим выражениям:

 

                                                (8)`

 

                                             

Случай 4 – модель с ограничением на производство и потребление. В качестве ограничений используются оба уравнения (6) и (7), поэтому нужно заменить  двумя множителями , чтобы можно было провести соответствующую модификацию модели. Тогда уравнение (2) приобретет вид

 

                                          (10),

 

а множители можно вычислить, подставляя  из уравнения (10) в уравнение (6) и (7) соответственно, что дает

 

                                         (11)

 

                                        (12)

 

Уравнение (11) и (12) можно решить итерационными методами. И модель четвертого случая позволяет найти простые оценки, остальные три модели сводятся к квадратным уравнениям относительно. Все четыре рассмотренные гравитационные модели были получены для независимых потоков товаров; на самом дели эти потоки должны быть взаимосвязаны. Часть потока продукта  из  в  может быть вызвана спросом, связанным с использованием производителями в  продукте  в качестве сырья.

Эту трудность можно частично преодолеть, если используемые варианты гравитационной модели включают в себя независимые оценки . Оценку этих величин можно получить с помощью регрессионного анализа. Независимые переменные в уравнениях регрессии относительно  могут включать в себя характеристики производства и потребления в регионах , и   продуктов, отличных от . Коэффициенты этих уравнений аналогичны технологическим коэффициентам в моделях «затраты - выпуск». [2]

Для оценки набора переменных потоков  при известных ограничениях в виде равенств необходимо максимизировать энтропию связанную с  распределения вероятностей, в результате чего получится наиболее вероятная оценка  (наиболее вероятный прогноз потока спроса продукта  из -го района в  –й район).

Для этого предварительно выясним вид функции , определяющей вид коэффициента  и зависящего от функции полезности. Обоснование выбора коэффициента  в гравитационной модели основывается на так называемой изопериметрической задаче вариационного исчисления. Мы находим наиболее вероятные значения потоков спроса продукта , производимого в регионе , потребителями в регионе  как решение задачи максимизации энтропии. В простейшем случае это выглядит следующим образом. Необходимо отыскать функцию , которая при данных условиях обеспечивает максимум энтропии

                                           (13)

В общем виде, применительно к нашим целям, задача сводится к отысканию  как функции , при которой интеграл

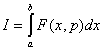                                                       (14)

принимает максимальное значение при условиях, что

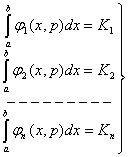                                                  (15)

где  - константы (заданы) и равенства (15) выражают ограничения, наложенные на интеграл (14). Соответствующая теорема вариационного исчисления гласит, что функция , обеспечивающая максимум интеграла (14), находится с помощью решения уравнения

                   (16)

Здесь  - неопределенные множители, которые находятся подстановкой , удовлетворяющей уравнению (16) в равенства (15).

Конкретизируя решение оптимизации гравитационной модели с учетом того, что мощности предприятий ограничены, т.е.

,                                                      (17)

найдем распределение вероятностей  при котором энтропия максимальна,

                                                   (18),

а условия, которые должны быть выполнены, суть нормирующее равенство

                                                                 (19)

и равенство 17 [2]

Итак,

                                                  (20)

                                                    (21)

                                                             (22)

                                                                    (23)

                                                        (24)

                                                                  (25)

Подставляя найденные величины в 16, получаем

                                                (26)

                                   (27)

Для того, чтобы исключить  и  подставим сначала найденное значение  в 19

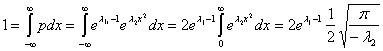                      (28)

откуда                                                                                                                 (29)

 должен быть отрицательным, иначе интеграл (28) не существует. Подставим 27 и 29 в (17).

;

 

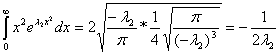                                   (30)

Следовательно

                                                              (31)

и                                       (32)

подставляя найденные величины в 27, находим функцию, для которой при заданных условиях энтропия максимальна:

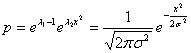                                              (33)

Собственно энтропия  находится подстановкой (33) в (13),

                                                       (35)

и что весьма полезно, что при заданной энтропии гауссовское (нормальное) распределение имеет наименьшую из всех одномерных распределений дисперсию.

Проведенные рассуждения говорят о том, что функция  при целевой функции полезности в виде максимума энтропии должны быть экспоненциального типа.

Рассмотрим 4-й случай – ограничено производство и потребление. Предположим, что на перевозку продукта  тратится величина . Тогда надо максимизировать

!

 

при ограничениях (6) и (7) и с учетом стоимостного ограничения

 

                                                        (36)

Решение данной задачи имеет вид

 

                                   (37)

 

где                                                                                                 (38)

 

                                

 

Величина  теоретически определяется через уравнение (36);

-при увеличении , уменьшается.

Аналогично можно получить решения для остальных трех случаев. Например, для случая 2 (ограничение на производство) по этой процедуре получим

 

                                             (39)

 

где                                                                                                           (40)

 

Здесь отсутствует член, как и в уравнениях (8) и (9). Это означает, что продукт  размещается между регионами (потребителями)  пропорционально «транспортной доступности»  по отношению к , которая характеризуется величиной . Возможны и другие характеристики региона  (отличные от «транспортной доступности»), которые делают более выгодным для  по сравнению с любым другим регионом ввозить продукт . Пусть, например,  - прибыль региона  от использования единицы продукта  по сравнению с использованием этой же единицы продукта любым другим регионом. Будем выбирать единицы измерения, так, чтобы они были непосредственно сопоставимы с транспортными затратами. Тогда уравнение (39) и (40) переписываются в виде

 

                           (41)

 

                          (42)

 

Величины  порождаются уровнем экономики в регионе , поэтому их можно приблизительно описать текущим уровнем потребления  в , а это есть. Обычно предположение в такой ситуации заключается в том, что прибыль пропорциональна логарифму единицы измерения, поэтому

 

                                                        (43),

 

где некоторый параметр. При подстановке  из уравнения (43) в уравнение (41) и (43) они переходят в уравнение (8) и (9) .

После приведенного обоснования приведенной гравитационной модели несложно полученные результаты распространяются на модель «затраты - выпуск», которая логично вытекает из теории экономической базы. Эта теория успешно применяется для местного и регионального прогноза, так как представляет собой наиболее простую формулировку взаимозависимости между экономическими секторами.

Определяются два сектора экономической активности, измерения которых проводятся в единицах занятости. Сектор 1 – базовой занятости, сектор 2 – небазовой занятости. Экономическая активность базовой занятости направлена на производство, ориентированное на внешние рынки (в других регионах или экспорт), а небазовый сектор производит товар для внутренних рынков.

Обозначим: - полная занятость,  - небазовая занятость,  – базовая занятость.

 или

 пусть, тогда                                                            (44)

 

Величина «» принимается константой. Вернемся к тому, что  - полный объем производства продукта . Он может потребляться внутренними секторами региона или внешним сектором «окончательного спроса» (экспорта). Для однорегиональной модели введем обозначения:

часть , обозначаемая через , потребляемая сектором ,а  потребляется секторам окончательного спроса. Тогда по всем  сектора внутреннего спроса

 

                                                    (45)

 

Величина продукта  на производство продукта

 

   и  

 

Пологая  =1, 2, получим систему уравнений, откуда

 

                                                        (46)

 

Здесь  - известная матрица технологических коэффициентов «затраты – выпуск»,  – единичная матрица. Уравнение (46) совпадает с (44), только в (44) - все величины скалярные, а в (46) – матрицы и векторы и уравнение (45) дает реалистическую оценку экономической структуры города или региона. При развитии модели на многорегиональный случай будем действовать по аналогии и основными результатами Леонтьева – Страута, в которых предполагается, что производителей не интересует окончательное распределение товаров, а потребителей – их происхождение. Это означает, что все товары, производимые в регионе , как бы поступают в общий фонд предложения, и все товары, потребляемые в , предварительно извлекаются из фонда потребления. Изобразим существенные потоки продукта  в модели Леонтьева – Страута.

 

 

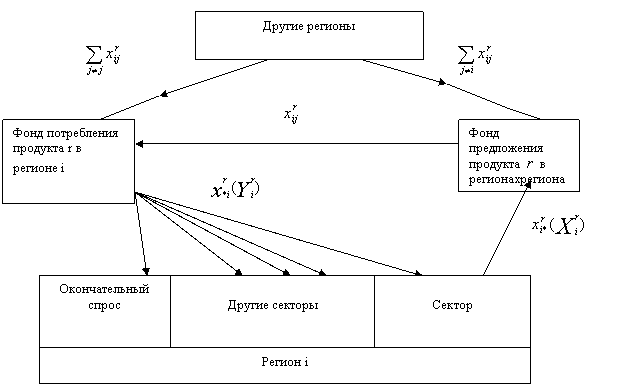
Рис. 1 Потоки продукта  в модели Леонтьева – Страута [3].

 

Отметим, что при одном регионе  должно выполняться равенство между , но в многорегиональной системе это уже не обязательно. Теперь  - это объем продукта , производимый в регионе  и перевозимый в фонд потребления в регионе .

Теперь каждый регион в отдельности должен удовлетворять соотношению «затраты – выпуск» типа (45) и соответствующая система уравнений согласно рис. 1 принимает вид

 

                                                    (47),

 

где        - количество продукта , используемое в регионе ;

- потребление сектором окончательного спроса в регионе ;

- количество продукта , используемое другими секторами (в этом выражении  - матрица технологических коэффициентов «затраты – выпуск» в регионе ).

Основными переменными являются , относительно которых следует искать решение, но здесь принимаются более слабые допущения: не только нельзя провести независимой оценки , но даже величину  нельзя оценить независимо. Предположения гравитационного типа допускаются, но предполагается, что  выполняется лишь при .

При этом система уравнений

 

;   

 

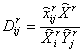
(где  - эмпирически оцениваемая функция расстояния) нелинейная по  и имеет столько уравнений, столько неизвестных (включая ). Она может быть решена приближенно при помощи предположения, что известны все потоки в некоторый базовый период; после этого их можно решить относительно приращений потоков в следующий период. Отсюда следует, что при заданном наборе окончательного спроса можно определить приращения потоков с точностью до величин первого порядка малости и использовать при краткосрочном прогнозе спроса.

Объединим модели «затраты – выпуск» и гравитационную модель, используя метод максимизации энтропии. Из четырех рассмотренных случаев рассмотрим только первый и последний (без ограничений и с ограничениями на спрос и производство). Для этого предположим для первого случая, что нет и независимой оценки для , что соответствует гипотезе Леонтьева и Страута. Единственным ограничением будет уравнение

 

                                                        (48)

Теперь будем рассматривать уравнение Леонтьева – Страута в качестве ограничения на . Запишем его в виде

 

                                         (49).

 

Максимизируем энтропию распределения вероятностей, связанного с  (здесь  переменный индекс, как и  и  ).  при ограничениях 48 и 49.

Для решения задачи запишем функцию Лагранжа

 

,

где  и  - множители Лагранжа, связанные с уравнениями (48) (49), соответственно. Теперь получим оценку , решая систему равнений  совместно с уравнениями (25) и (26). Будем иметь

 

                               (50)

 (единица включена в множитель ).

Множитель Лагранжа  получается подстановкой  в уравнении (25), множитель Лагранжа  находится подстановкой  из (50) в уравнении (49), что дает          (51)

Обозначим                                                                                        (52)

                                                             (53)

тогда                                                                                  (54)

Перепишем уравнение (51) в более компактном виде

 

 

и из него получим 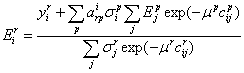                                              (55)

Это уравнение нельзя решить в явном виде. Используя итерационную процедуру: задать , вычислить из уравнения (54), вычислить из уравнения (55) и продолжить процедуру пока процесс не сойдется. С помощью уравнений (52) и (53) выражение (50) для  может быть переписано в виде

                                             (56)

Таким образом, с помощью метода максимизации энтропии первый случай в модели Леонтьева – Страута описывается уравнениями (56),(55),(54). Произведение  обеспечивает согласованность потоков с уравнением Леонтьева – Страута. Из уравнения (32) следует, что размерность этого произведения совпадает с размерностью единицы измерения количества продукта  и гравитационная модель (56) является простейшей: величины  пропорционально .

В четвертом наиболее реальном с точки зрения практики случае, где есть ограничения на производство и потребление в роли ограничений одновременно выступают уравнения (8) и (9) вместе с модифицированными уравнениями (36) и (49). Поэтому  заменим на , а  - на , что дает

                                                  (57)

Теперь  в (57) не входит, следовательно, наши предположения отделяют ту часть модели, которая связана с моделью «затраты - выпуск», от гравитационной части. Отсюда следует, что процедуры, используемые для оценки  и , должны быть такими, чтобы удовлетворялось уравнение (57); тогда потоки спроса можно оценить с помощью гравитационной модели 37 - 38^¢

Выводы: в реальной ситуации имеется множество различных товаров, некоторые из них являются промежуточными, другие конечными; прогнозировать спрос на одни и другие можно лишь на основе гибридной гравитационной модели, которая будет получена с помощью метода максимизации энтропии на следующем этапе исследований. При этом центральным вопросом остается возможность оценки величин  и  независимо от процедуры оценки . Поскольку при различных исходных предположениях получается различные модели, то наиболее важный вывод состоит в том, что включаемые в модель гипотезы должны подвергаться всесторонней проверки.

 

 

1.                 А. Дж. Вильсон. Энтропийные методы моделирования сложных систем. М.: «Наука», 1978.

2.                 С. Голдман. Теория информации. М.: И.Л., 1957

3.                 Leontief W., Strout A. Multi – regional input – output analysis. – In: Structural Futerdependence and Economic Deuelopment /Ed. T.Barna, Macmillan, London, 1963.