УДК 621.313.001.2(075.8)
ПРИМЕНЕНИЕ ЗАКОНОВ КИРХГОФА ДЛЯ РАСЧЕТА ТЕПЛОМАССООБМЕННЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ МАШИНАХ
Марасанов В.В., Корень Е.В.
Электромеханическое преобразование энергии в электрических машинах сопровождается преобразованием электрической или механической энергии в тепло. Какова же часть энергии теряется бесполезно, и каким образом можно снизить эти потери? Для ответа на поставленные вопросы сначала выясним, какие возникают потери энергии при работе электрических машин, а затем приведем пример теплового расчета, основанного на методе тепловых схем замещения. Данный метод использует понятия тепловых сопротивлений, рассчитываемых по правилам для электрических цепей (законам Кирхгофа). Он получил широкое распространение при проектировании электрических машин, в результате его использования определяются средние превышения температуры отдельных элементов. Мощность потерянной энергии называют потерями мощности или просто потерями. Потери в электрических машинах подразделяются на основные и добавочные [1]. Основные потери возникают в результате происходящих в машине основных электромагнитных и механических процессов, а добавочные потери обусловлены различными вторичными явлениями. Во вращающихся электрических машинах основные потери подразделяются на:
1. механические потери,
2. магнитные потери, или потери в стали,
3. электрические потери.
Механические потери состоят из: 1) потерь в подшипниках, 2) потерь на трение щеток о коллектор или контактные кольца и 3) вентиляционных потерь, которые включают в себя потери на трение частей машины о воздух и другие потери, связанные с вентиляцией машины (мощность кинетической энергии отходящего воздуха и потери в вентиляторе). В ряде случаев электрические машины охлаждаются не воздухом, а водородом или водой, и соответствующие потери также относят к вентиляционным. Потери в подшипниках зависят от типа подшипников (качения или скольжения), от состояния трущихся поверхностей, вида смазки и т.д. Потери на вентиляцию зависят от конструкции машины и рода вентиляции. В каждой данной машине механические потери определяются суммой трех видов потерь и зависят только от скорости вращения и не зависят от нагрузки [1].
Магнитные потери включают в себя потери на гистерезис и вихревые токи, вызванные перемагничиванием сердечников активной стали.
Электрические потери возникают в обмотках. Они определяются их сопротивлениями, зависящими от температуры.
Для увеличения коэффициента полезного действия эксплуатируемых электрических машин необходимо знать максимально допустимые средние превышения температуры их элементов. Применение метода эквивалентных тепловых схем замещения в методике теплового расчета позволяет нам это сделать.
В тепловом расчете электрической машины ставится задача определить превышение температуры различных частей машины над температурой охлаждающей среды. Превышение температуры частей электрической машины над температурой охлаждающей среды определяется выражением
![]() , (1)
, (1)
где ![]() - температура рассматриваемой части электрической машины;
- температура рассматриваемой части электрической машины;
![]() - температура охлаждающей среды.
- температура охлаждающей среды.
В общем случае передача тепла идет тремя путями: теплопроводностью, конвекцией и излучением.
Основными источниками выделения тепла в электрической машине являются обмотки, стальные части магнитной цепи и конструктивных элементов, в которых возникают потери от перемагничивания. Необходим также учет нагрева скользящего контакта. Механические потери, включая вентиляционные, обычно имеют меньшее значение.
На пути движения тепловых потоков от источника тепла происходит перепад температуры в активных частях машины, толще изоляции и между охлаждающими поверхностями и охлаждающей средой. В тепловом расчете определяются эти внутренние перепады и превышения температуры внешней поверхности охлаждаемых частей электрической машины над температурой охлаждающего воздуха. При непосредственном соприкосновении материала обмоток с охлаждающей средой, т.е. при непосредственном охлаждении проводников обмотки, определяется превышение температуры металла обмотки над температурой охлаждающего газа или жидкости.
Перепадом температуры в толще металла обмотки и магнитопровода часто пренебрегают, так как теплопроводность металлов в сотни раз больше теплопроводности изоляции.
В практических расчетах ограничиваются определением среднего превышения температуры обмоток, т.е. допускают, что температура обмоток в стали пакетов статора (ротора) в рассматриваемых объемах постоянна.
Отвод тепла с поверхности нагретого тела происходит путем излучения в окружающее пространство (лучеиспусканием), передачи тепла путем теплопроводности, передачи его путем конвекции.
В чистом виде теплопередача путем излучения может иметь место, если нагретая поверхность находится в вакууме. Теплопередача путем теплопроводности воздуха (или другого газа) настолько мала, что ее практически невозможно учесть.
Конвективная теплопередача обусловлена нагревом воздуха, соприкасающегося с нагретой поверхностью электрической машины и вследствие этого совершающего восходящее движение. Его место занимает более холодный воздух, который, в свою очередь, нагревается и движется вверх. Конвективную теплопередачу сильно повышает принудительное увеличение скорости движения воздуха (искусственный обдув нагретой поверхности). В практических расчетах нагрева электрических машин обычно применяют упрощенные формулы, определяющие перепад температуры между нагретой поверхностью и охлаждающим газом, которые учитывают все виды теплоотдачи с поверхности, имеющие место при охлаждении электрических машин.
Для применения законов Кирхгофа установим соответствие между электрическими параметрами цепи и теплотехническими параметрами схем замещения электрических машин (таблица 1).
Таблица 1
Таблица соответствия электрических и тепловых величин в уравнениях Кирхгофа
|
Величины, соответствующие электрическим схемам |
Величины, соответствующие тепловым схемам |
|
Сила тока I, A |
Тепловой поток Q, Вт |
|
Сопротивление R, Ом |
Сопротивление R, |
|
Напряжение U, В |
Разность средних температур 1-й и 2-й частей машины |
Применяя метод тепловых схем замещения, можно использовать как понятия тепловых сопротивлений, так и тепловых проводимостей, рассчитываемых по правилам для электрических цепей. Как уже было отмечено, применение тепловых схем замещения дает возможность определять средние температуры частей электрической машины, принимаемых за однородные тела.
Второй закон Кирхгофа для электрических цепей определяется выражением
![]() , (2)
, (2)
где Ik – силы токов в ветвях цепи, А;
Rk – сопротивления ветвей цепи, Ом;
εk – электродвижущие силы источников тока, В.
Для каждой части тепловой схемы справедливо основное уравнение
![]() , (3)
, (3)
где ![]() - тепловой поток между точками 1 и 2 схемы, представляющими 1-ю и 2-ю части машины, Вт;
- тепловой поток между точками 1 и 2 схемы, представляющими 1-ю и 2-ю части машины, Вт;
![]() - средние температуры этих частей,
- средние температуры этих частей, ![]() ;
;
![]() - тепловое сопротивление между точками 1 и 2 схемы,
- тепловое сопротивление между точками 1 и 2 схемы, ![]() / Вт [3].
/ Вт [3].
Естественно, что чем большее число эквивалентных элементов может быть предложено для замены отдельных частей электрической машины, тем точнее окажется расчет. Однако усложнение тепловой схемы, а следовательно, и расчета должно сочетаться с достижимой точностью расчета при имеющейся неопределенности исходных данных.
На примере статора машины переменного тока рассмотрим построение тепловой схемы замещения [3]. Разбиваем статор на три условно однородные в тепловом отношении тела, являющиеся источниками тепла: пазовая часть обмотки статора с потерями Рп, две стороны лобовых частей с суммарными потерями Рл и стальной сердечник статора с потерями Рс.
Каждая часть создает тепловые потоки. Считая в общем случае, что условия охлаждения рассматриваемых частей машины различны, принимаем четыре пути рассеяния тепла (рис.1, а): Qиз – тепловой поток к стенкам зубцов сердечника с перепадом температуры в тепловом сопротивлении пазовой изоляции Rиз; Qк – тепловой поток к охлаждающему воздуху в радиальных вентиляционных каналах через тепловое сопротивление Rк; ![]() и
и ![]() - тепловые потоки от пазовой части обмотки с перепадом температуры в тепловых сопротивлениях
- тепловые потоки от пазовой части обмотки с перепадом температуры в тепловых сопротивлениях ![]() вдоль проводников обмотки. Лобовые части обмотки рассеивают со своих поверхностей тепловые потоки
вдоль проводников обмотки. Лобовые части обмотки рассеивают со своих поверхностей тепловые потоки ![]() и
и ![]() с перепадом температуры в тепловых сопротивлениях
с перепадом температуры в тепловых сопротивлениях ![]() . Поверхности сердечника статора рассеивают тепловые потоки
. Поверхности сердечника статора рассеивают тепловые потоки ![]() и
и ![]() с боковых сторон пакетов с перепадом температуры в тепловых сопротивлениях
с боковых сторон пакетов с перепадом температуры в тепловых сопротивлениях ![]() и поток Qс.р в радиальном направлении с наружной поверхности ярма статора и внутренней поверхности статора при общем тепловом сопротивлении Rс,р.
и поток Qс.р в радиальном направлении с наружной поверхности ярма статора и внутренней поверхности статора при общем тепловом сопротивлении Rс,р.
В случае одинаковой температуры охлаждающего воздуха у теплорассеивающих поверхностей тепловой расчет можно вести по схеме замещения, приведенной на рис.1, б. В этом случае тепловые сопротивления Rпр, Rл представляют собой параллельно соединенные сопротивления ![]() и соответственно
и соответственно ![]() :
:
![]() , (4)
, (4)
а сопротивление Rс – параллельно соединенные сопротивления ![]() и Rс,р:
и Rс,р:
![]() , (5)
, (5)
где ![]() .
.
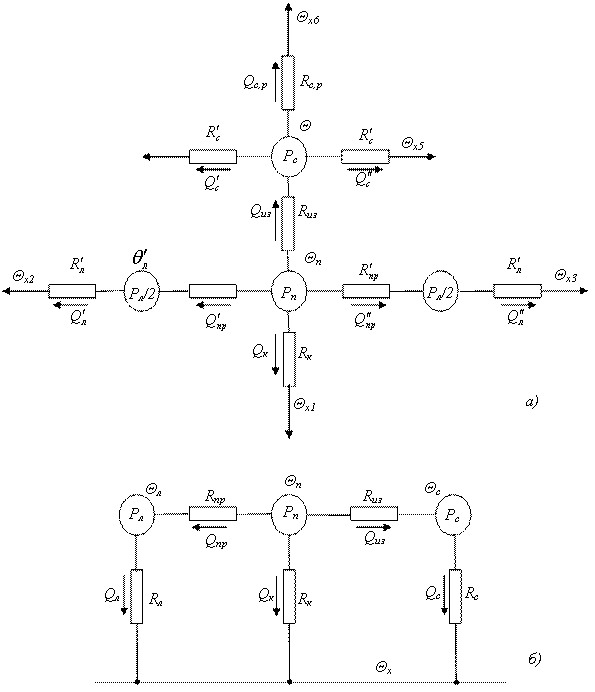
Рис.1. Тепловая схема замещения статора машины переменного тока.
а – при различных температурах воздуха у теплорассеивающих поверхностей; б – при одинаковой температуре охлаждающего воздуха.
В схеме на рис.1, б имеется восемь неизвестных: θп, θл, θс – средние температуры пазовой части обмотки, лобовых частей и сердечника статора; Qиз, Qпр, Qк, Qл и Qс – тепловые потоки, упомянутые выше. Для определения этих неизвестных составим в соответствии с рис.1, б систему уравнений:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; (6)
; (6)
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В результате совместного решения этих уравнений находим средние температуры отдельных частей статора, равные превышениям температур, если θx=0.
Нами была разработана методика теплового расчета для закрытых асинхронных двигателей с короткозамкнутым ротором типа беличьей клетки без циркуляции внутреннего воздуха.
Предлагаемая методика позволяет проводить качественную оценку нагрева двигателей с выше указанными конструктивными особенностями. Для более точного отражения физической сути тепловых процессов в асинхронном двигателе в методике предусмотрен расчет нагрева элементов двигателей, для которых с достаточной точностью могут быть заданы исходные данные и определены зависимости для расчета коэффициентов теплоотдачи. При этом были приняты следующие допущения:
- в поперечном сечении двигателей отсутствует перетекание тепла, что позволяет решать плоскую задачу в продольном сечении;
- в поперечном сечении обмотки температуры отдельных проводников равны средней температуре в рассматриваемом сечении;
- коэффициенты теплопроводности электротехнических материалов и воздуха считаем постоянными для рабочих температур частей двигателя;
- тепловыми потоками через клинья пазов статора и вал пренебрегаем.
Тепловая эквивалентная схема замещения электродвигателей с короткозамкнутым ротором приведена на рис.2.
При тепловом расчете электродвигателей учитываются все греющие потери, генерируемые в двигателе. Для выбранной тепловой схемы замещения потери в обмотках статора и ротора распределены пропорционально длинам участков лобовых и пазовых частей. Короткозамкнутый ротор представлен в виде одного тела, в источник потерь включены потери в обмотке ротора и добавочные потери в роторе. Принято, что источники (греющие потери) сосредоточены в середине рассматриваемых элементов.
По тепловой схеме замещения была составлена система уравнений для расчета превышения температуры короткозамкнутых двигателей без циркуляции внутреннего воздуха. Поскольку для подобного расчета можно использовать как тепловые сопротивления, так и тепловые проводимости, то мы при составлении схемы и системы уравнений по ней имели дело с последними (![]() - тепловые проводимости,
- тепловые проводимости, ![]() - превышения температуры элементов машин, Р – потери мощности).
- превышения температуры элементов машин, Р – потери мощности).
Система уравнений для расчета превышения температуры короткозамкнутых двигателей без циркуляции внутреннего воздуха имеет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; (7)
; (7)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - превышение температуры соответственно в пазовой части обмотки статора; в лобовой части обмотки статора со стороны наружного вентилятора; в лобовой части обмотки статора со стороны привода; в сердечнике статора; в зубцах статора; внутреннего воздуха со стороны наружного вентилятора; внутреннего воздуха со стороны привода; участка станины, расположенного над пакетом статора, ротора; концевых участков станины со стороны наружного вентилятора; щита, расположенного со стороны наружного вентилятора; концевых участков станины со стороны привода; щита, расположенного со стороны привода; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора у подшипникового щита со стороны наружного вентилятора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора в концевой части станины со стороны наружного вентилятора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора над пакетом статора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора в концевой части станины со стороны привода;
- превышение температуры соответственно в пазовой части обмотки статора; в лобовой части обмотки статора со стороны наружного вентилятора; в лобовой части обмотки статора со стороны привода; в сердечнике статора; в зубцах статора; внутреннего воздуха со стороны наружного вентилятора; внутреннего воздуха со стороны привода; участка станины, расположенного над пакетом статора, ротора; концевых участков станины со стороны наружного вентилятора; щита, расположенного со стороны наружного вентилятора; концевых участков станины со стороны привода; щита, расположенного со стороны привода; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора у подшипникового щита со стороны наружного вентилятора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора в концевой части станины со стороны наружного вентилятора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора над пакетом статора; наружного охлаждающего воздуха для двигателей габарита 56-350 за исключением двигателей с форсированным охлаждением ротора в концевой части станины со стороны привода;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - проводимость соответственно между пазовой и лобовой частями обмотки статора со стороны наружного вентилятора; между пазовой и лобовой частями обмотки статора со стороны привода; между обмоткой и спинкой статора; между обмоткой и зубцами статора; от лобовых частей обмотки к внутреннему воздуху для двигателей габарита 56-355 без циркуляции внутреннего воздуха со стороны наружного вентилятора; для двигателей с гофрированной станиной – со стороны внутреннего; от лобовых частей обмотки статора к внутреннему воздуху для двигателей габарита 56-355 без циркуляции внутреннего воздуха со стороны привода; для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; спинки пакета статора к станине; между зубцами и спинкой статора; между ротором и зубцами статора; от лобовых частей обмотки ротора к внутреннему воздуху со стороны наружного вентилятора; от лобовых частей обмотки ротора к внутреннему воздуху со стороны привода; от внутреннего воздуха к концевой части станины со стороны наружного вентилятора, для двигателей с гофрированной станиной – со стороны внутреннего; от внутреннего воздуха к подшипниковым щитам со стороны наружного вентилятора; от внутреннего воздуха к концевой части станины со стороны привода, для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; от внутреннего воздуха к подшипниковым щитам со стороны привода; от подшипникового щита к наружному воздуху со стороны наружного вентилятора; соединения «щит-станина» со стороны наружного вентилятора; от подшипникового щита к наружному воздуху со стороны привода; соединения «щит-станина» со стороны привода; между элементами станины; от станины к наружному воздуху на концевом участке со стороны наружного вентилятора; между элементами станины; от станины к наружному воздуху над пакетом статора; от станины к наружному воздуху на концевом участке со стороны привода; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора;
- проводимость соответственно между пазовой и лобовой частями обмотки статора со стороны наружного вентилятора; между пазовой и лобовой частями обмотки статора со стороны привода; между обмоткой и спинкой статора; между обмоткой и зубцами статора; от лобовых частей обмотки к внутреннему воздуху для двигателей габарита 56-355 без циркуляции внутреннего воздуха со стороны наружного вентилятора; для двигателей с гофрированной станиной – со стороны внутреннего; от лобовых частей обмотки статора к внутреннему воздуху для двигателей габарита 56-355 без циркуляции внутреннего воздуха со стороны привода; для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; спинки пакета статора к станине; между зубцами и спинкой статора; между ротором и зубцами статора; от лобовых частей обмотки ротора к внутреннему воздуху со стороны наружного вентилятора; от лобовых частей обмотки ротора к внутреннему воздуху со стороны привода; от внутреннего воздуха к концевой части станины со стороны наружного вентилятора, для двигателей с гофрированной станиной – со стороны внутреннего; от внутреннего воздуха к подшипниковым щитам со стороны наружного вентилятора; от внутреннего воздуха к концевой части станины со стороны привода, для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; от внутреннего воздуха к подшипниковым щитам со стороны привода; от подшипникового щита к наружному воздуху со стороны наружного вентилятора; соединения «щит-станина» со стороны наружного вентилятора; от подшипникового щита к наружному воздуху со стороны привода; соединения «щит-станина» со стороны привода; между элементами станины; от станины к наружному воздуху на концевом участке со стороны наружного вентилятора; между элементами станины; от станины к наружному воздуху над пакетом статора; от станины к наружному воздуху на концевом участке со стороны привода; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора; между элементами наружного воздуха, обдувающего станину с форсированным охлаждением ротора;![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - потери соответственно в пазовой части обмотки статора; в лобовых частях обмотки статора со стороны наружного вентилятора, для двигателей с гофрированной станиной – со стороны внутреннего; в лобовых частях обмотки статора со стороны привода, для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; в спинке статора; в зубцах статора; в короткозамкнутом роторе; внутренние механические потери со стороны внутреннего вентилятора (или щеточного узла); внутренние механические потери со стороны, противоположной внутреннему вентилятору (или щеточному узлу); на трение в подшипниках со стороны наружного вентилятора; на трение в подшипниках со стороны привода.
- потери соответственно в пазовой части обмотки статора; в лобовых частях обмотки статора со стороны наружного вентилятора, для двигателей с гофрированной станиной – со стороны внутреннего; в лобовых частях обмотки статора со стороны привода, для двигателей с гофрированной станиной – со стороны, противоположной внутреннему вентилятору; в спинке статора; в зубцах статора; в короткозамкнутом роторе; внутренние механические потери со стороны внутреннего вентилятора (или щеточного узла); внутренние механические потери со стороны, противоположной внутреннему вентилятору (или щеточному узлу); на трение в подшипниках со стороны наружного вентилятора; на трение в подшипниках со стороны привода.
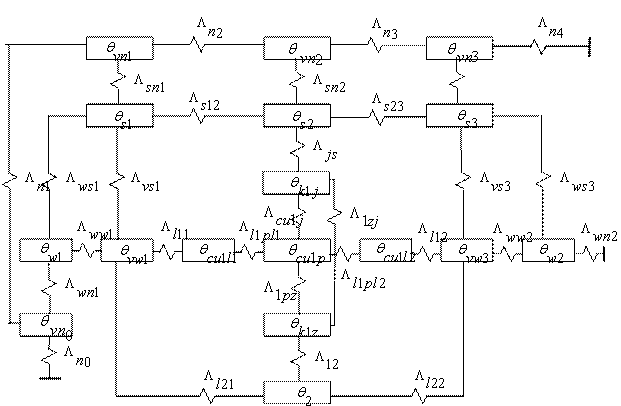
Рис. 2 Тепловая схема электродвигателя с короткозамкнутым ротором.
Полученную систему уравнений можно решить с помощью компьютерных программ, например программы «Математика 5.0».
На основе изложенного можем сделать выводы:
1) применение законов Кирхгофа в тепловых расчетах электрических машин, основанных на методе тепловых схем замещения, позволяет определить средние превышения температуры элементов данных машин;
2) максимальные превышения температуры в обмотках асинхронных двигателей определяются путем решения уравнения теплопроводности с использованием результатов решения эквивалентных тепловых схем замещения;
3) результаты теплового расчета позволят использовать электрические машины в различных отраслях производства при различных режимах работы.
The possibility of present the electrical machine as a plan of warm replace was presented. Also law of Kirxgof can be use for calculate of warm floods. Two variants of determinate were discribed: with warm resistors and with warm conductions.
1. Вольдек А.И. Электрические машины. Учебник для студентов высш. техн. учеб. заведений. Изд. 2-е, перераб. и доп. – Л.: Энергия, 1974. – 840с.
2. Гурин Я.С., Кузнецов Б.И. Проектирование серий электрических машин. – М.: Энергия, 1978. – 480с.
3. Проектирование электрических машин: Учеб. пособие для вузов/И.П. Копылов, Ф. А. Горяинов, Б.К. Клоков и др.; Под ред. И.П. Копылова. – М.: Энергия, 1980. – 496с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.