УДК 628.543.49
МАТЕМАТИЧНА МОДЕЛЬ ПРОЦЕСУ ГОРІННЯ ПРИРОДНОГО ГАЗУ З РЕЦИРКУЛЯЦІЄЮ ПРОДУКТІВ ЗГОРАННЯ ДЛЯ ЦІЛЕЙ УПРАВЛІННЯ
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К.
Задача управління процесом спалювання природного газу формулюється і вирішується як оптимізаційна [1]. Існуючі системи автоматичного управління горінням, що змінюють коефіцієнт надлишку повітря впливом на співвідношення "паливо – повітря" з корекцією за вмістом у димових газах кисню, недостатньо ефективні, особливо для високоефективних топкових пристроїв. Розповсюджені системи автоматичного регулювання процесом горіння з корекцією за вмістом кисню або продуктів недопалу, які виходять з топкових пристроїв, оптимізують процес тільки з огляду на повноту згорання, то б то вирішується лише задача мінімізації суми втрат з газами, які виходять з топкових пристроїв, і хімічною неповнотою згорання. Додаткове врахування утворення в процесі горіння токсичних продуктів згорання змушує переглянути традиційну формалізацію задачі оптимізації процесу горіння та ввести в розгляд одночасно два критерії, що враховують економічність і токсичність процесу горіння. Один зі способів згортки критеріїв приводить до адитивного узагальненого критерію оптимізації, вираженого через склад продуктів згорання.
Крім того, актуальною, на наш погляд, є задача дослідження додаткових (крім співвідношення "паливо – повітря") впливів, що можуть бути використанні для управління процесом горіння з метою зниження токсичності продуктів згорання, одним з яких є спалювання природного газу з рециркуляцією продуктів згорання. Експериментальних даних за повним складом продуктів згорання природного газу з рециркуляцією димових газів у топкових пристроях практично немає.
На основі якісного аналізу можна припустити, що такі процеси мають низку суттєвих відмін у порівнянні зі спалюванням газу у чистому повітрі. По-перше, запалення та горіння проходить у середовищі зі зніженим вмістом кисню та підвищеною кількістю баластних газів. По-друге, вміст кисню може бути змінним. По-третє, гази рециркуляції, які надходять до топки, містять токсичні компоненти, які додатково впливають на остаточну токсичність продуктів згорання.
Такий критерій у виді суми двох доданків, що враховують екологічні фактори й економічність процесу горіння, причому кожний з доданків представлено у виді безрозмірних комплексів [2], має вид:
![]() (1)
(1)
де ![]() - критерій, що характеризує економічність
процесу горіння,
- критерій, що характеризує економічність
процесу горіння,
де ![]() - концентрація водню, оксиду вуглецю та кисню
у димових газах;
- концентрація водню, оксиду вуглецю та кисню
у димових газах;![]() - допустимі значення концентрацій відповідних
компонентів.
- допустимі значення концентрацій відповідних
компонентів.
![]() - критерій, що характеризує токсичність процесу горіння,
- критерій, що характеризує токсичність процесу горіння,
де ![]() - поточне значення оксиду вуглецю та оксиду
азоту;
- поточне значення оксиду вуглецю та оксиду
азоту; ![]() - гранично допустимі викиди відповідних
компонентів.
- гранично допустимі викиди відповідних
компонентів.
Доцільність використання узагальненого критерію для автоматичної оптимізації процесу горіння визначається тим, що практично всі його складові залежать від співвідношення "паливо - повітря", найважливішого фактора, що визначає режим горіння та ступінь рециркуляції.
Оскільки всі складового критерію виражаються через склад продуктів згорання, то, узагальнений критерій оптимізації вимагає знання практично повного складу димових газів. У даний час із усіх компонентів газів, що виходять з топкових пристроїв, що враховуються критерієм, є можливість вимірювати лише кисень і продукти недопалу (водень і окис вуглецю).
Для дослідження процесу горіння природного
газу з рециркуляцією продуктів згорання розроблена математична модель, яка
побудована на методі розрахунку рівноважних продуктів реакцій, що дозволяє отримати
достатньо докладний склад димових газів [3]. Математична модель є системою з
трьох груп рівнянь хімічної рівноваги: рівнянь дисоціації, матеріального
балансу та рівняння закону Дальтона. Для розрахунку температури горіння ці
рівняння необхідно доповнити рівнянням енергетичного балансу топкового пристрою.
У даній статті приведені результати розрахункових досліджень процесу горіння
природного газу Шебелинського родовища у вихлопних газах топкових пристроїв
наступного складу: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для опису рівноважної багатокомпонентної гетерогенної реагуючої системи потрібно задати два скінчених списки [4]:
- список d речовин, що беруть участь у
реакціях - ![]() ,
, ![]() , що включають речовини
, що включають речовини ![]() в атомарному стані, f речовин у молекулярному стані так що q+f
= d;
в атомарному стані, f речовин у молекулярному стані так що q+f
= d;
- список D реакцій між d
речовинами ![]() , що задаються стехіометричною матрицею
, що задаються стехіометричною матрицею![]() :
:
![]() (2)
(2)
Якщо в якості одного з допущень прийняти, що система являє собою суміш ідеальних газів, даному наборові реакцій відповідно до термодинамічного закону діючих мас однозначно відповідає D рівнянь дисоціації [2]:
![]() (3)
(3)
де ![]() - парціальний тиск і-й речовині в
суміші;
- парціальний тиск і-й речовині в
суміші;![]() - константа рівноваги j-й реакції;
- константа рівноваги j-й реакції;
та q рівнянь закону збереження маси, записуваного для кожного ![]() - го елемента у складі вихідної речовини:
- го елемента у складі вихідної речовини:
![]() (4)
(4)
де ![]() - елемент атомарної матриці
- елемент атомарної матриці ![]() , що показує число атомів
, що показує число атомів ![]() -го елемента в і -й речовині;
-го елемента в і -й речовині; ![]() ,
, ![]() - число молів
- число молів ![]() - го елемента відповідно у паливі та окислювачі;
- го елемента відповідно у паливі та окислювачі; ![]() - мольний стехіометричний коефіцієнт;
- мольний стехіометричний коефіцієнт; ![]() - число молів вихідної речовини.
- число молів вихідної речовини.
Таким чином, запису рівноважного
багатокомпонентного процесу у виді (2) відповідає математична модель, що
складається з ![]() нелінійних рівнянь (3) і (4), а також
рівняння закону Дальтона:
нелінійних рівнянь (3) і (4), а також
рівняння закону Дальтона:
![]() (5)
(5)
де P - тиск суміші газів.
Використання списку реакцій (2)
застосовуються рекомендації і стехіометричні рівняння, приведені в роботі [1,
4, 5], яким відповідає математична модель виду (3)...(5), що дозволяє розрахувати
12 - ть найбільш ймовірних компонентів продуктів згорання: ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . З них
. З них ![]() ,
, ![]() ,
, ![]() визначають економічність процесу згорання,
визначають економічність процесу згорання, ![]() ,
, ![]() - його токсичність.
- його токсичність.
Матриця стехіометричних коефіцієнтів ![]() і рівнянь дисоціації, що відповідають
обраному спискові реакцій, представлені у таблиці 1. Атомарна матриця
і рівнянь дисоціації, що відповідають
обраному спискові реакцій, представлені у таблиці 1. Атомарна матриця ![]() - у таблиці 2.
- у таблиці 2.
Число молів ![]() та
та ![]() у випадку завдання рідкого палива ваговими
частками хімічних елементів (табл. 1) розраховується при виборі умовної
молекулярної маси паливної і повітряної суміші [4] за формулами:
у випадку завдання рідкого палива ваговими
частками хімічних елементів (табл. 1) розраховується при виборі умовної
молекулярної маси паливної і повітряної суміші [4] за формулами:
![]() (6)
(6)
![]() , (7)
, (7)
де ![]() ,
, ![]() - вагові частки
- вагові частки ![]() - го елемента в і – й речовини відповідно у паливі й окислювачі;
- го елемента в і – й речовини відповідно у паливі й окислювачі;
![]() - умовна молекулярна маса палива й окислювача;
- умовна молекулярна маса палива й окислювача;
![]() - атомна маса
- атомна маса ![]() - го елемента; n, m - кількість речовин відповідно у паливі й
окислювачі, що містять
- го елемента; n, m - кількість речовин відповідно у паливі й
окислювачі, що містять![]() - й елемент;
- й елемент; ![]() ,
, ![]() - кількість атомів
- кількість атомів ![]() - го елемента в і - й речовині, що
входить відповідно у паливо й окислювач.
- го елемента в і - й речовині, що
входить відповідно у паливо й окислювач.
Мольний стехіометричний коефіцієнт найбільш зручно визначити за універсальною формулою [5]:
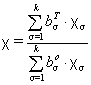 , (8)
, (8)
де ![]() - валентність
- валентність ![]() - го елемента; k
- кількість елементів, що реагують при горінні палива.
- го елемента; k
- кількість елементів, що реагують при горінні палива.
Значення констант дисоціації ![]() , що входять у рівняння (3), звичайно
задаються інтерполяційними формулами в залежності від температури, тому в
розглянутій моделі до системи рівнянь хімічної рівноваги (3)...(8) додається
рівняння енергетичного балансу топки [6], що дозволяє визначити адіабатичну температуру
горіння:
, що входять у рівняння (3), звичайно
задаються інтерполяційними формулами в залежності від температури, тому в
розглянутій моделі до системи рівнянь хімічної рівноваги (3)...(8) додається
рівняння енергетичного балансу топки [6], що дозволяє визначити адіабатичну температуру
горіння:
![]() (9)
(9)
де ![]() - нижча теплота згорання палива;
- нижча теплота згорання палива; ![]() - тепло, внесене в топку окислювачем;
- тепло, внесене в топку окислювачем; ![]() - втрата тепла з хімічною неповнотою
згорання;
- втрата тепла з хімічною неповнотою
згорання; ![]() - об'ємна теплоємність продуктів згоряння;
- об'ємна теплоємність продуктів згоряння; ![]() - обсяг димових газів;
- обсяг димових газів; ![]() - адіабатична температура горіння,
- адіабатична температура горіння, ![]() - коефіцієнт рециркуляції;
- коефіцієнт рециркуляції; ![]() - температура газів рециркуляції.
- температура газів рециркуляції.
Докладний опис складових рівняння (9) приведено в нормативному методі розрахунку котлових агрегатів [6].
Оскільки теплоємність продуктів згорання ![]() залежить від заданої температури
залежить від заданої температури ![]() , рівняння (9) вирішується ітераційним
методом.
, рівняння (9) вирішується ітераційним
методом.
Після розрахунку адіабатичної температури горіння, визначається максимальна температура смолоскипа за формулою [7] :
![]() (10)
(10)
де В0 - критерій Больцмана, що визначається з вираження [7]:
![]() (11)
(11)
де dГ - діаметр амбразури пальника, м.
Таблиця 1
Матриця стехіометричних коефіцієнтів реакцій горіння та рівняння дисоціації
|
Речовина, елемент |
Відповідні реакціям горіння рівняння дисоціації |
||||||||||||
|
Елемент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
-1 |
-2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
2 |
-2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
|
|
|
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
-2 |
1 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
2 |
|
|
|
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
Таблиця 2
Атомарна матриця регулюючий системи, що наведена у таблиці 1
|
Елемент |
Речовина, елемент |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
2 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
2 |
1 |
2 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
0 |
1 |
Параметр b знаходиться з рівняння[7]:
![]() (12)
(12)
де ![]() - швидкість повітря в амбразурі пальника, приведена до
273 К, м/с.
- швидкість повітря в амбразурі пальника, приведена до
273 К, м/с.
![]() (13)
(13)
де GВ - витрата повітря, що визначається з виразу:
![]() (14)
(14)
де ВГ - витрата палива, м3/с; l - число пальників.
При максимальній температурі продуктів згорання у
смолоскипі розраховуються значення ![]() . Рішення системи рівнянь (3)…(12) дозволяє визначити рівноважні концентрації
продуктів згорання
. Рішення системи рівнянь (3)…(12) дозволяє визначити рівноважні концентрації
продуктів згорання ![]() .
.
Рішення системи рівнянь енергетичного балансу
виконується методом Мюллера і дозволяє оцінити адіабатичну температуру горіння.
Температура в ядрі полум'я ![]() визначається за алгоритмом В.А. Крутієві [7].
визначається за алгоритмом В.А. Крутієві [7].
Табличні дані залежності констант дисоціації від температури апроксимовані багатоступеневими поліномами. Коефіцієнти поліномів визначається методом найменших квадратів.
Після оцінки значень констант дисоціації здійснюється розрахунок складу продуктів згорання методом Ньютона.
За допомогою моделі, проведено розрахункове дослідження процесу горіння палива з рециркуляцією димових газів та у повітрі при однакових умовах роботи топкового пристрою.
Досліджено вплив на склад продуктів згорання співвідношення "паливо - окислювач", при різних коефіцієнтах витрати окиснення. Результати приведені на рис.1, 2 за групами компонентів.
На рисунку 1 показана зміна складу компонентів, що характеризують економічність процесу горіння при перемінному коефіцієнті витрати окислювача.
У діапазоні ![]() мається залишкова концентрація продуктів неповного згорання (
мається залишкова концентрація продуктів неповного згорання (![]() ,
, ![]() ), що обумовлено явищем дисоціації. Їхнє догорання відбувається дуже
повільно, незважаючи на наявність надлишкового кисню, причому кількість
), що обумовлено явищем дисоціації. Їхнє догорання відбувається дуже
повільно, незважаючи на наявність надлишкового кисню, причому кількість ![]() та
та ![]() при горінні з рециркуляцією димових газів мало відрізняється від
згорання палива у повітрі.
при горінні з рециркуляцією димових газів мало відрізняється від
згорання палива у повітрі.
Однак спостерігається й істотна відмінність.
Процес повного згорання природного газу з рециркуляцією димових газів
зміщується убік дещо більших значень коефіцієнта витрати окислювача (![]() ) у порівнянні з горінням у повітрі. Ймовірний
вмісту надлишкового кисню при
) у порівнянні з горінням у повітрі. Ймовірний
вмісту надлишкового кисню при ![]() у 2, 4 рази нижче змісту кисню при горінні у повітрі.
у 2, 4 рази нижче змісту кисню при горінні у повітрі.
Вміст окису азоту з рециркуляцією димових газів у порівнянні з горінням у повітрі знижується в 2-4 рази в залежності від значення коефіцієнта витрати окислювача. Це можна пояснити падінням температури горіння та кількості надлишкового кисню у газах, що виходять з топкових пристроїв.
Наведені дослідження показали, що умови оптимального згорання природного газу з рециркуляцією продуктів згорання при мінімізації топкових втрат та токсичності димових газів суттєво відрізняються від горіння у чистому повітрі: процес повного згорання "зміщується" убік дещо більших значень коефіцієнта витрати окислювача за рахунок зменшення концентрації кисню у продуктах згорання, при цьому викиди токсичних компонентів суттєво знижуються, наприклад, концентрація оксиду азоту знижується у 3...4 рази, концентрація двооксиду вуглецю – на 8...12 відсотків.
Різний характер зміни концентрацій компонентів димових газів від коефіцієнтів надлишку повітря та рециркуляції вимагає більш ретельного вибору режиму горіння, точного визначення оптимального управління, як що порівнювати його з горінням у чистому повітрі, що у кожному окремому випадку обирається рішенням задачі оптимізації.
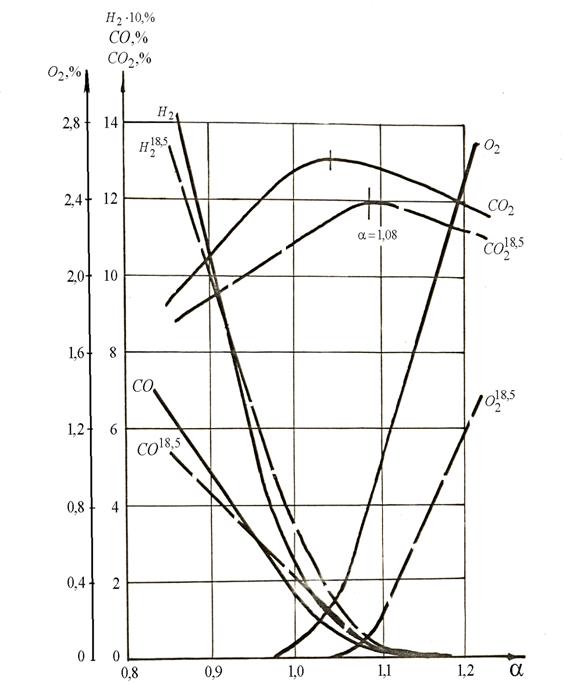
Рис. 1 Зміна складу компонентів, що характеризують економічність процесу горіння при перемінному коефіцієнті витрати окислювача
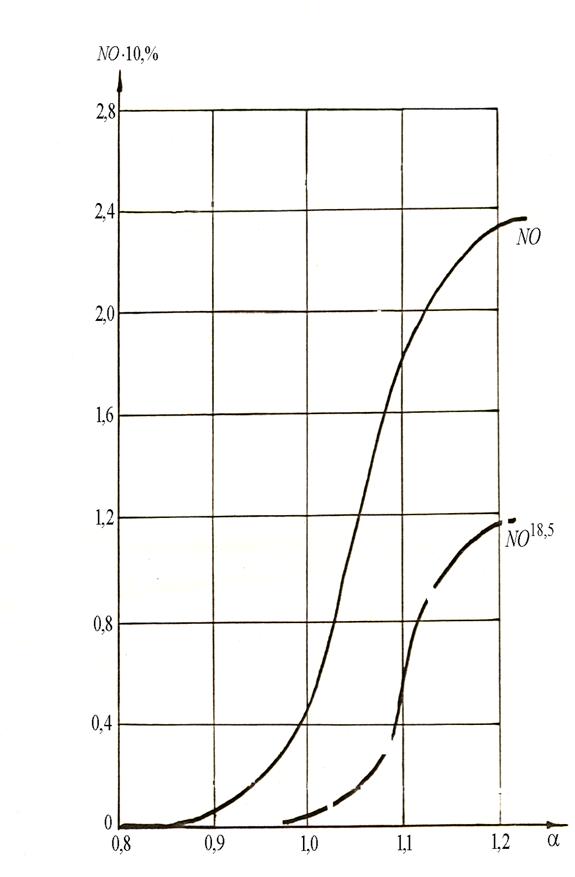
Рис. 2 Зміна складу окису азоту у продуктах спалення при перемінному коефіцієнті витрати окислювача
The article deals with the process of burning of the natural gas with the recirculation of products of combustion on the basis of solutions of the accepted system of equations of chemical thermodynamics which allows to define rather a detailed composition of smoke gases. The results allow to solve the questions of control of the process of burning on the basis of the generalized ecological economic criterion of optimization.
1. Цирульников Л.М. О возможности оптимизации топочного процесса в газомазутных котлах. – Теплоэнергетика, 1979, №6, с. 52-54.
2. Рыжиков Ю.Г., Тодорцев Ю.К. Минимизация токсичности выбросов при управлении сжиганием мазута в топках паровых котлов. Сб. научных трудов №109. – М. Моск. энерг. ин-т, 1986. С. 44-50.
3. Киреев В.А. Методы практических расчетов в термодинамике химических реакций. – М. Химия, 1975.
4. Лушпа А.И. Основы химической термодинамики и кинетики химических реакций. – М.: Машиностроение, 1981. – 240 с.
5. Алемасов В.Е. Теория ракетных двигателей. – М.: Гостехиздат, 1963, - 476 с.
6. Тепловой расчет котельных агрегатов (Нормативный метод). Под ред. Кузнецова и др. – М.: Энергия, 1973. – 296 с.
7. Офердиев Т.Б. Образование оксидов азота в газомазутных парогенераторах. – Теплоэнергетика, 1975, № 9
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.