УДК 62-69
ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ЭЛЕКТРИЧЕСКИХ НАГРЕВАТЕЛЕЙ ПО КРИТЕРИЮ ЭКОНОМИИ ЭНЕРГИИ
Попруга А.Г.
Цель исследований: установить взаимосвязь между параметрами провода и коэффициентом полезного действия электрического нагревателя, предложить конструкцию нагревателя с повышенным коэффициентом полезного действия.
Современный уровень: данная работа является продолжением статьи [5] и посвящена разработке математической модели электрического нагревателя с целью уменьшения потерь энергии.
Постановка задачи исследований: разработать математическую модель электрического нагревателя и экспериментально подтвердить ее адекватность.
Теоретическая часть:
Пусть энергия подается к нагревателю, изготовленному из нихромовой проволоки круглого сечения с сопротивлением ZН:
ZН = RН + ј ω LН , (1)
где LН – индуктивность провода нагревателя; RН – активное сопротивление провода нагревателя; ω – угловая частота.
При прохождении тока по линии передачи и нагревателю в каждом участке этих проводников выделяется тепло. Электрическая энергия транспортируется от источника к нагревателю по диэлектрику вдоль проводов линии передачи.
Провода в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике.
Для характеристики плотности потока энергии в теории Максвелла вводится вектор Пойнтинга – Умова ![]() , который равен векторному произведению векторов
, который равен векторному произведению векторов ![]() :
:
![]() (2)
(2)
где ![]() – напряженности магнитного и электрического полей на поверхности провода нагревателя соответственно.
– напряженности магнитного и электрического полей на поверхности провода нагревателя соответственно.
Если величина вектора Пойнтинга положительна, то энергия поступает в провод нагревателя из внешнего пространства и идет на изменение магнитного поля в объеме провода и на выделение теплоты в нем. Если вектор Пойнтинга имеет отрицательную величину, то поток энергии направлен от провода нагревателя в окружающее его пространство. При этом энергия, запасенная в магнитном поле в объеме провода, частично возвращается в окружающее провод пространство и частично преобразуется в теплоту.
Такие колебания с частичным возвратом энергии в пространство, окружающее провод, можно рассматривать как результат наличия внутреннего реактивного сопротивления XН провода нагревателя.
Как известно, между реактивным XН и активным RН сопротивлениями цепи и разностью фаз φ между напряжением и током в этой цепи существует соотношение[4]:
tg φ = XН / RН (3)
Из уравнения (3) следует, что для уменьшения фазового сдвига φ
между напряжением и током в нагревателе необходимо уменьшать реактивное сопротивление XН = ω LН и увеличивать активное сопротивление RН нагревателя.
Протекание тока по электрической цепи нагревателя сопровождается потреблением энергии от источника. Скорость поступления энергии характеризуется мощностью. Нагреватель потребляет от источника мощность РП:
РП = U∙I (4)
Непосредственно в виде теплоты в нагревателе выделяется мощность РН:
РН = U∙I∙cosφ (5)
Коэффициент полезного действия нагревателя:
ηн = РН / РП = U∙I∙cosφ / U∙I = cosφ (6)
Таким образом, представляется целесообразным рассмотреть теорему Пойнтинга - Умова в комплексной форме с целью определения активного и внутреннего индуктивного сопротивлений провода нагревателя.
В теории Максвелла доказывается, что вектор Пойнтинга ![]() совпадает с направлением движения энергии электромагнитного поля, а его величина равна количеству энергии проходящей за 1сек. через единичную площадку нормальную направлению переноса. Вектор Пойнтинга имеет размерность мощности [В·А / М2] или энергии в единицу времени, отнесенной к единице поверхности.
совпадает с направлением движения энергии электромагнитного поля, а его величина равна количеству энергии проходящей за 1сек. через единичную площадку нормальную направлению переноса. Вектор Пойнтинга имеет размерность мощности [В·А / М2] или энергии в единицу времени, отнесенной к единице поверхности.
При синусоидальных сигналах Е и Н можно записать:
H = Н m sin (ω t + φ H) (7)
E = E m sin (ω t +φ E) (8)
При переходе от действительной синусоидальной функции (оригинала) к изображающей комплексной величине получим:
H m sin (H =ω t + φ H) → ![]() =
=![]() (9)
(9)
E m sin (ω t + φ E) →![]()
![]() =
= ![]() (10)
(10)
Комплексный вектор Пойнтинга определим как:
![]() (11)
(11)
обозначения ![]() означают, что напряженности E и H изменяются по синусоидальному закону и являются векторными функциями;
означают, что напряженности E и H изменяются по синусоидальному закону и являются векторными функциями;
Активное и внутреннее индуктивное сопротивление проводников при переменном токе определяется с помощью комплексного вектора Пойнтинга:
![]() =I2RH+jI2XH=I2ZH (12)
=I2RH+jI2XH=I2ZH (12)
Откуда:
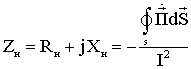
![]() (13)
(13)
Для установления взаимосвязи между током ![]() , напряженностью магнитного поля
, напряженностью магнитного поля ![]() и напряженностью электрического поля
и напряженностью электрического поля ![]() рассмотрим распределение тока в цилиндрическом проводе круглого сечения.
рассмотрим распределение тока в цилиндрическом проводе круглого сечения.
В соответствии с законом Ома в дифференциальной форме:
![]() , (14)
, (14)
где ![]() - плотность тока, направленная по напряженности электрического поля; γ- удельная проводимость материала провода нагревателя.
- плотность тока, направленная по напряженности электрического поля; γ- удельная проводимость материала провода нагревателя.
Соотношение (14) устанавливает связь между плотностью тока в данной точке проводящей среды и напряженностью поля в этой же точке[3].
Первое и второе уравнения Максвелла для проводящей среды имеют вид:
![]() (15)
(15)
![]()
![]()
![]() , (16)
, (16)
где μа - магнитная проницаемость материала провода нагревателя.
Умножим правую и левую часть (16) на γ и с учетом (14) получим:
![]() (17)
(17)
![]() (18)
(18)
Возьмем ротор от уравнения (18):
![]() (19)
(19)
В установившемся режиме:
![]()
Поэтому:
![]() (20)
(20)
Раскроем ![]() в цилиндрической системе координат:
в цилиндрической системе координат:
![]()
![]() (21)
(21)
Введением новой переменной:
![]() (22)
(22)
Уравнение (21) преобразуется к виду:
![]() (23)
(23)
Уравнение (23) является частным случаем уравнения Бесселя [1].
Решение уравнения (23) можно записать следующим образом:
![]() (24)
(24)
где A и B - постоянные интегрирования; J0(X) – функция Бесселя нулевого порядка первого рода; N0(X) – функция Бесселя нулевого порядка второго рода.
Постоянные A и B определяются из граничных условий при r = 0 и r = R, т.е. при X = 0 и ![]()
Функция N0(X) обладает той особенностью, что при Х = 0 (т.е. на оси провода при r = 0) она обращается в бесконечность. Но из физических соображений ясно, что ![]() на оси провода не может иметь бесконечно большое значение, поэтому слагаемое BN0(X) в решении (24) отбрасываем (принимая В = 0). Следовательно:
на оси провода не может иметь бесконечно большое значение, поэтому слагаемое BN0(X) в решении (24) отбрасываем (принимая В = 0). Следовательно:
![]()
![]() (25)
(25)
Функцию J0(X) можно представить в виде ряда:
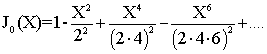 =
= 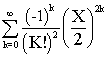 (26)
(26)
Постоянная А равна комплексной амплитуде плотности тока ![]() на оси провода. Следовательно:
на оси провода. Следовательно:
![]() (27)
(27)
Функция J0(X) есть комплексное число, так как Х в соответствии с (22) является комплексным числом. Через b0 обозначен модуль, а через β0 - аргумент комплексного числа J0(X) [2].
Напряженность магнитного поля может быть получена из уравнения:
![]() (28)
(28)
Откуда:
![]()
![]() (29)
(29)
Подставим (22) в (29) и после несложных преобразований получим:
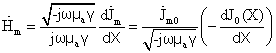 (30)
(30)
Дифференцируя ряд (26) находим:
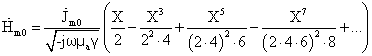
![]()
![]()
![]() =
=
=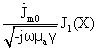 =
= 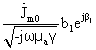 (31)
(31)
Через b1 обозначен модуль, а через β1 – аргумент комплексного числа J1(X).
По аналогии с (26) представим J1(X) в виде:
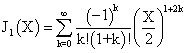
![]()
![]() (32)
(32)
Комплексное сопротивление Z провода нагревателя длиной L определится выражением [3]:
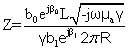 =
= 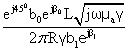 (33)
(33)
Уравнение (33) можно переписать в другой форме:
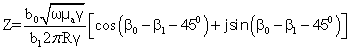 (34)
(34)
Откуда следует:
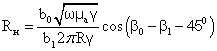 (35)
(35)
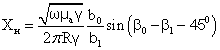 (36)
(36)
После подстановки (22) в (26) и (32) и с учетом того, что ![]() определим для ряда значений
определим для ряда значений ![]() модули b0,b1 и аргументы β0, β1 функций Бесселя, а также tgφ, cosφ, где φ = β0-β1-450 где φ – угол, на который запаздывает по фазе напряженность магнитного поля относительно напряженности электрического поля на поверхности провода. Результаты вычислений приведены в табл.1.
модули b0,b1 и аргументы β0, β1 функций Бесселя, а также tgφ, cosφ, где φ = β0-β1-450 где φ – угол, на который запаздывает по фазе напряженность магнитного поля относительно напряженности электрического поля на поверхности провода. Результаты вычислений приведены в табл.1.
Таблица 1.
![]()
|
|
b0 |
β0 |
b1 |
β1 |
tgφ |
cosφ |
|
0.1 |
1 |
0.143 |
0.049 |
-44.977 |
0.0021 |
1 |
|
0.2 |
1 |
0.573 |
0.1 |
-44.576 |
0.0026 |
1 |
|
0.3 |
1 |
1.261 |
0.15 |
-44.462 |
0.0126 |
0.9999 |
|
0.4 |
1.001 |
2.292 |
0.2 |
-44.003 |
0.0226 |
0.9997 |
|
0.5 |
1.001 |
3.558 |
0.25 |
-43.201 |
0.0307 |
0.9995 |
|
0.6 |
1.002 |
5.157 |
0.3 |
-42.284 |
0.0426 |
0.9991 |
|
0.7 |
1.003 |
6.99 |
0.35 |
-41.539 |
0.0617 |
0.9981 |
|
0.8 |
1.007 |
9.167 |
0.401 |
-40.451 |
0.0808 |
0.9968 |
|
0.9 |
1.01 |
11.516 |
0.451 |
-39.248 |
0.1009 |
0.9949 |
|
1 |
1.015 |
14.267 |
0.502 |
-37.873 |
0.1253 |
0.9922 |
|
2 |
1.229 |
52.254 |
1.041 |
-16.73 |
0.4449 |
0.9137 |
|
3 |
1.951 |
96.52 |
1.8 |
+15.699 |
0.7218 |
0.8108 |
|
4 |
3.439 |
138.21 |
3.173 |
+53.915 |
0.8183 |
0.7733 |
|
5 |
6.231 |
178.911 |
5.809 |
+93.552 |
0.8498 |
0.7620 |
|
6 |
11.501 |
219.649 |
10.85 |
+133.43 |
0.8760 |
0.7522 |
|
7 |
21.547 |
260.271 |
20.5 |
+173.526 |
0.8924 |
0.7461 |
|
8 |
40.818 |
300.928 |
39.07 |
+213.69 |
0.9080 |
0.7404 |
|
9 |
77.957 |
341.493 |
74.974 |
+253.957 |
0.9175 |
0.7369 |
|
10 |
149.85 |
382.12 |
144.67 |
+294.293 |
0.9269 |
0.7334 |
![]()
Экспериментальная часть:
С целью практического подтверждения полученных теоретических результатов был проведен эксперимент с использованием шестиплечного моста (рис.1)
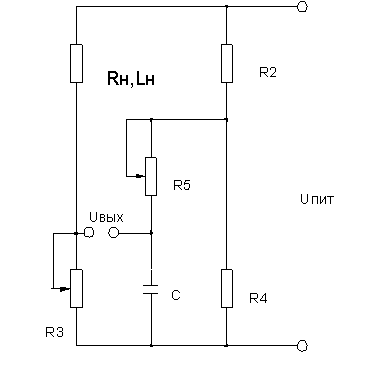
Рис.1
Измерению подвергались два провода, изготовленные из нихрома диаметром 0.1мм и 0.4мм. Указанные провода длиной 1м поочередно подключались к мостовой схеме изображенной на рис.1.
Измерения проводились цифровым мультиметром модели ЕС890D, который подсоединялся к клеммам Uвых. мостовой схемы.
а) Измерение активного, индуктивного сопротивлений и
удельной проводимости нихромового провода
При измерении активного сопротивления Rн и индуктивности Lн провода диаметром 0.4мм использовались такие элементы мостовой схемы: R2, R4 - МЛТ-0.25 номиналом 360 Ом, С - К73-17 номиналом 0.47 мкФ, R3 - СП5-15 номиналом 10 Ом, R5 - СП5-15 номиналом 10 Ом. Питание мостовой схемы U = 8B, 50 Гц. Результаты измерения следующие: Rн = 9.5 Ом, Lн = 1.64·10-3 Гн.
Используя выражение:
![]() (37)
(37)
Определим γ:
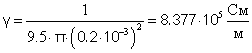
При аналогичных измерениях нихромового провода диаметром 0.1мм в мостовой схеме использовался резистор R3 - СП5-15 номиналом 220 Ом. Результаты измерений в этом случае такие: Rн = 133 Ом, Lн = 6.25·10-3 Гн, γ = 9.573·105 См/м.
б) Измерение абсолютной магнитной проницаемости μа
нихромового провода.
Индуктивность Lн нихромового провода определяется абсолютной магнитной проницаемостью, μа нихрома и геометрическими размерами
провода.
Индуктивность Lн нихромового провода длиной l выражается формулой:
![]() (38)
(38)
Формула (38) справедлива только при условии равномерного распределения тока по сечению провода, т.е. только при постоянном токе.
Схема установки для испытания нихромового провода, с целью определения абсолютной магнитной проницаемости µа, приведена на рис.2.
Испытанию подвергались два нихромовых провода диаметром 0.4мм и 0.1мм.
Нихромовые провода последовательно закреплялись на специальной линейке длиной 1м. С помощью переключателя S1,типа П1Т-1-1, на провод диаметром 0.1мм подавалось напряжение 13.3В, сопротивление Rи выбиралось равным 1Ом. Падение напряжения на Rи измерялось с помощью осциллографа С1-97, и фиксировалась постоянная времени τ установления тока I в цепи,τ = 0.05·10-3 с.
В результате определяем Lн:
Lн = τ·Rн = 0.05·10-3 ·133 = 6.65·10-3 Гн.
а из выражения (38) определяем µа:
µа = 6.65·10-3 ·8·π = 0.167.

![]() Рис. 2
Рис. 2
Аналогично на провод диаметром 0.4мм подавалось напряжение 9.5В, сопротивление Rи выбиралось равным 0.1 Ом. Постоянная времени установления тока I в цепи для этого случая τ = 0.2·10-3 с.
Индуктивность Lн и абсолютная магнитная проницаемость, µа для этого случая равны:
Lн = 0.2·10-3 ·9.5 = 1.9·10-3 Гн.
µа = 1.9·10-3 ·8·π =0.048.
в) Проверка адекватности теоретических результатов и экспериментальных данных
Для провода диаметром 0.4мм на основании экспериментальных данных определим величину:
R![]()
Далее по формуле (26) определим J0(X):
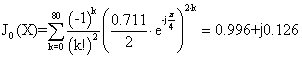
Вычисляем коэффициенты b0,β0:
![]()
![]()
Вычисляем по формуле (32) J1(X):
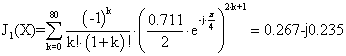
Вычисляем коэффициенты b1,β1:
![]()
![]()
![]()
По формулам (35),(36) вычисляем Rн, Хн:
![]()
![]()
![]()
Вычислим значение индуктивности Lн:
![]()
Аналогично проведем расчет для провода диаметром 0.1мм:
![]()
![]()
J0(X) = 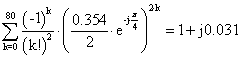
![]()
![]()
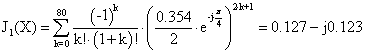
![]()
![]()
![]()
![]()
![]()
![]()
Выводы:
1. В работе предложена математическая модель для исследования электрических нагревателей из различных материалов и сечений с высокой степенью адекватности практическим результатам.
2. С целью повышения коэффициента полезного действия электрический нагреватель необходимо изготавливать из системы параллельно соединенных нагревателей малого сечения. ![]()
In article on the basis of theory Maxwell, theorem Pointing-Umov, the equation and functions Bessel the mathematical model is developed for definition active and internal inductive resistance of a cylindrical wire of a heater. For confirmation of adequacy of mathematical model results of experiments by definition of active, inductive resistance, magnetic permeability, specific conductivity nihrom wires of two various diameters are resulted.
1. Несис Е.И. Методы математической физики.- М.: Просвещение, 1977.- 199с.
2. Абрамовиц М., Стиган И. Справочник по специальным функция.-М.: Наука, 1979.- 832с.
3. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле.- М.: Высш. школа,1978.-231с.
4. Нейман Л.Р., Демирчян К.С Теоретические основы электротехники. Том 2.- Л.: Энергоиздат,1981.- 416с.
5. Попруга А.Г. Усовершенствование электрических нагревателей по критерию экономии энергии // Вестник Херсонского национального технического университета.- 2003.-№ 2(12).- С. 142-145. ![]()
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.