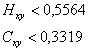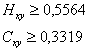Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.3.01:519.67

МУЛЬТИФРАКТАЛЬНЫЙ МЕТОД АВТОМАТИЗИРОВАННОГО РАСПОЗНАВАНИЯ ПОМЕХ НА ИЗОБРАЖЕНИИ

Полякова М.В., Крылов В.Н.

Постановка проблемы. Автоматизированные системы обработки и распознавания изображений в медицинской диагностике, производственном контроле, радиолокации, астрономических и биологических исследованиях часто сталкиваются с необходимостью обработки зашумленных изображений. Основными источниками шума на цифровом изображении являются процесс передачи изображения, а также процесс его получения (оцифровка) [1]. Работа датчиков зависит от их качества и от различных внешних факторов в процессе видеосъемки. Например, при оцифровке изображения с помощью матрицы приборов с зарядовой связью основными факторами, определяющими величину шума, являются уровень освещенности и температура датчиков. При передаче изображений помехи возникают и в каналах связи.

Диапазон шумов, встречающихся при обработке изображений, достаточно широк [1, 2]. Например, при статистическом моделировании собственных шумов датчиков, которые возникают из-за недостаточного освещения и/или высокой температуры, в большинстве случаев используется аддитивная гауссовская модель с плотностью вероятности шума

,                               (1)

где I — значение интенсивности изображения, — параметры распределения.

Импульсный шум возникает, когда в процессе получения изображения имеют место быстрые переходные процессы, например, неправильная коммутация. При моделировании импульсного шума значение интенсивности каждой точки изображения с вероятностью Р_а  заменяется на значение а, с вероятностью Р_b — на значение b и с вероятностью 1–(Р_а+ Р_b), где Р_а+Р_b≤1, остается неизменной. Плотность вероятности импульсного шума

                               (2)

где  - -функция.

В системах, использующих естественное освещение, часто возникают пространственные изменения освещенности, которые являются причиной мультипликативной помехи на изображении. Она моделируется операцией

                                                                                          (3)

где  — полутоновое изображение,  — отражающая способность объекта,  — освещенность объекта,  — пространственные координаты. Для того чтобы структура и оценки параметров системы автоматизированной  идентификации шума были обоснованными, необходимо выбрать модель помеховой ситуации. С учетом шумовых факторов в [1] статистическая модель изображения  представляется как  где , определяются формулой (3),  — аддитивный гауссовский шум с плотностью вероятности (1),  — импульсная помеха с плотностью распределения (2). Т. к. на объект, прежде всего, воздействует освещенность, а затем он подвергается воздействию датчиков, то собственные шумы датчика и переходные процессы получения изображения вызывают гауссовский и импульсный шум на неравномерно освещенном изображении, которое описывается произведением отражающей способности объекта и его освещенностью . Тогда статистическую модель помеховой ситуации, которая используется в данной работе, представим в виде:

Для подавления каждого из перечисленных видов помех существуют особые методы предварительной обработки изображений, однако помеховую ситуацию оценивает специалист в области распознавания изображений в неавтоматизированном режиме. Очевидно, что неавтоматизированная идентификация шума требует от оператора квалификации эксперта. Неточная оценка помеховой ситуации или параметров шума могут привести к некачественной предварительной обработке. Это обусловлено тем, что при выборе метода предварительной обработки и его параметров необходима априорная информация о процессе формирования изображений. Часто такая информация отсутствует, поэтому параметры метода предварительной обработки изображений подбираются путем настройки, которая не весгда позволяет отразить помеховую ситуацию. Это влияет на дальнейший процесс обработки изображений. Например, недооценка уровня мультипликативной помехи вызывает большие разрывы контуров объектов изображений при решении задачи контурной сегментации. Это, в свою очередь, влияет на ошибку распознавания этих объектов. Завышенная оценка уровня аддитивной гауссовской помехи ведет к размыванию контуров объектов, что также отражается на ошибке распознавания.

В этом случае оценка параметров мультипликативного шума осуществляется путем анализа спектра изображения или на основе исходного изображения. Анализ в автоматизированном режиме возможен тогда, когда шумовые пики ярко выражены или имеется априорная информация относительно расположения частотных составляющих. При решении в неавтоматизированном режиме задачи идентификации аддитивной помехи на изображении параметры функции плотности вероятности шума могут быть известны исходя из технических характеристик датчиков. Однако часто необходимо оценить эти параметры для конкретной системы, использованной при получении изображения. Если система доступна для исследования, то получают набор изображений однородных тестовых объектов, по которой оценивают параметры плотности вероятности. В противном случае, когда имеются только изображения, сформированные этой системой, вид функции плотности вероятности шума оценивают из гистограммы небольших участков изображения примерно постоянной яркости. Значение интенсивности на таких участках используют для вычисления параметров распределения шума.

Поэтому актуальной является проблема автоматизации процедуры идентификации шума на изображениях. Решение этой проблемы соответствует государственным научно-техническим программам, которые сформулированы в законе Украины «Про научную и научно-техническую деятельность» и в законе Украины «Про национальную программу информатизации».

Анализ последних публикаций. Нерешенные части общей проблемы. Задачу автоматизированной идентификации помех на изображении сформулируем следующим образом. Пусть задано исходное пространство признаков Х размерностью p=MN, представляющее значения интенсивности матрицы дискретных отсчетов изображения, где М — количество строк, N — количество столбцов этой матрицы. Необходимо найти преобразованное пространство Y, элементами которого являются p₁-мерные векторы, причем  p₁<p. Формально эта задача заключается в определении отображения А: , которое исходному пространству Х ставит в соответствие искомое пространство Y [3]. Решение задачи идентификации помехи на изображении сводится к определению вида помехи и оценки параметров шума.

Автоматизированная и автоматическая идентификация помех в последнее время являлась предметом активных исследований. При идентификации конкретного вида помехи используется статистическая обработка сигналов и скрытые марковские модели [4]. Если шум представляет собой смесь нескольких видов помех, то в задаче его автоматизированной идентификации используются модели смеси распределений, параметры которых определяются из условия оптимизации по некоторому критерию [5].

Изображения в общем случае содержат элементы широкого интервала масштабов, поэтому для их анализа целесообразно применять статистики, зависящие от масштаба, т. е. проводить многомасштабный статистический анализ в отличие от гауссовых статистик. Этот анализ может применяться как в случае стационарных, так и в случае нестационарных данных для характеристики их поведения. Частным случаем многомасштабного статистического анализа является мультифрактальный анализ данных [6], исследующий степенную зависимость свойств статистик от масштаба. Известно, что мультифрактальные показатели принимают разные значения для импульсного и гауссовского процессов, а также для детерминированных гладких функций, с помощью которых моделируется мультипликативная помеха на изображении [6]. Это дает основание для построения мультифрактального метода идентификации шумов изображений.

Целью данной работы являлась разработка мультифрактального метода автоматизированной идентификации шумов изображений. При достижении поставленной цели решены следующие задачи:

¾    разработка мультифрактального метода идентификации шумов изображений;

¾    исследование характеристик разработанного метода  на тестовых изображениях.

Изложение основного материала. При анализе зависимости статистической информации от масштаба данных используется два подхода: структурные функции и сингулярные меры [6]. Под структурными функциями понимают статистические моменты абсолютных разностей, зависящие от масштаба на некотором интервале его значений. Приведем определение структурной функции для одномерных данных, представляющих значение интенсивности i-го столбца изображения , где N  — число пикселей в столбце изображения.

Разностью r-го порядка функции  называется

                                                                   (4)

Определим степенную зависимость  момента порядка  ^t от масштаба r как

                                                         , ,                                (5)

где  — означают усреднение по переменной х.

В случае  структурная функция  отражает фрактальную структуру графика  который рассматривается как самоаффинный геометрический объект в двумерном евклидовом пространстве. На основании этого в [6] введен мультифрактальный показатель

где  — фрактальная размерность графика . Это означает, что 1 — наибольшее возможное значение для Н₁, которое достигается для почти всюду дифференцируемых функций. Если  Н₁=0,  — стационарный процесс, график которого заполняет пространство. Т. о. Н₁ позволяет оценить нестационарность . Т. к. мультипликативный шум моделируется детерминированной функцией пространственных координат и по своей природе нестационарен, для его отличия от стационарного гауссовского и импульсного шума целесообразно применять мультифрактальный показатель Н₁.

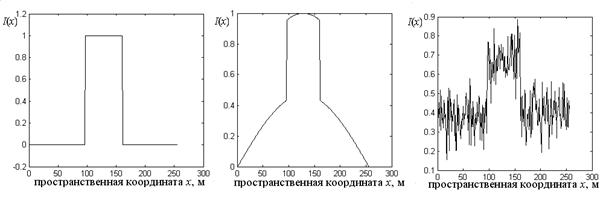
            На рис. 1 показан характер зависимости мультифрактального показателя Н₁  от вида помехи для столбца тестового изображения, содержащего один объект. Н₁ в этих случаях равно 1,0133; 0,99685; 0,0038969 соответственно.

а)                                                 б)                                               в)

Рис. 1 Значения интенсивности столбца тестового изображения (а) и они же для изображения, пораженного мультипликтивной (б) и гауссовской (в) помехой.

Для вычисления Н₁ в результате логарифмирования (5) получаем

                                                                   (6)

где С — некоторая константа. Значение  находим путем определения параметров линейной регрессионной зависимости  от .

Другим подходом к мультифрактальному анализу данных являются сингулярные меры, представляющие собой локально усредненный модуль градиента изображения.

В основе определения сингулярной меры лежит понятие нормализованной разности 1-го порядка. Ее значения вычисляются в каждой точке столбца изображения по формуле

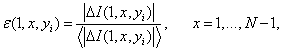
где

Пусть масштаб r принимает значения 1, 2, 4, …, N. Тогда сингулярная мера  определяется как

Определим функцию , выражающую степенную зависимость сингулярной меры от масштаба по формуле

  , .                          (7)

В смысле сингулярных мер значения интенсивности изображения характеризуются мультифрактальным показателем

Наибольшее значение С₁, равное 1, достигается для случайно расположенных -функций, вся энергия которых  сконцентрирована в отдельных точках. Случай  (наименьшему значению) достигается для случайно расположенных функций Хевисайда. Т. о. мультифрактальный показатель С₁ характеризует уровень импульсного шума на изображении. Поэтому его целесообразно применять для различения гауссовского и импульсного шума.

На рис. 2 показан характер зависимости мультифрактального показателя С₁  от вида помехи для столбца тестового изображения, содержащего один объект. С₁ в этих случаях равно 1,062; 0,72959; 0,10688 соответственно.

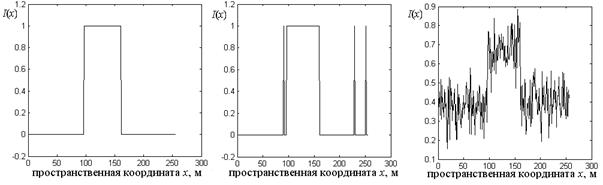
а)                                               б)                                               в)

Рис. 2 Значения интенсивности столбца тестового изображения (а) и они же для изображения, пораженного импульсной (б) и гауссовской (в) помехой.

Для вычисления С₁ в результате логарифмирования (7) имеем

                                                                                  (8)

где  — некоторая константа. Значение С₁ определяем как аппроксимацию производной функции в точке .

Приведенные определения структурной функции и сингулярной меры позволяют вычислять мультифрактальные показатели Н₁ и С₁ для одномерных данных. Для обработки изображений, представленных матрицами дискретных отсчетов интенсивности необходимо обобщить определения мультифрактальных показателей Н₁, С₁  на двумерный случай. Введем показатели Н₁, С₁  по направлениям x, y и обозначим их Н_х, С_х, Н_у, С_у соответственно. При определении Н_х, С_х  разности r-го порядка вычисляются и усредняются по столбцам изображения. Для С_х также по столбцам изображения усредняются значения сингулярной меры. При вычислении Н_у, С_у обработка производится по строкам изображения.

Показатели Н_х, Н_у, С_х, С_у характеризуют изотропный шум на изображениях или анизотропный шум горизонтального или вертикального направления. Если шум, например, мультипликативный, имеет диагональное направление, то показателей Н_х, Н_у, С_х, С_у недостаточно для его характеристики. Введем диагональные показатели Н_ху, С_ху следующим образом.

Пусть в (5) при вычислении разностей r-го порядка используется соотношение

                .                    (9)

Тогда (5) принимает вид:

,

а .

Для определения показателя С_ху предположим, что разность 1-го порядка вычисляется по формуле (9). Тогда нормализацию разности 1-го порядка произведем по формуле

,

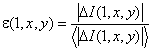где .

Если масштаб r принимает значения 1, 2, 4, …, N, то (7) принимает вид

, ,

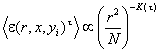а мультифрактальный показатель С_ху =, причем  [7].

С использованием построенных мультифрактальных показателей определим пространство признаков для идентификации помех на изображении. Сформируем параметры, которые целесообразно включить как компоненты  в вектор признаков. В качестве таких характеристик в работе выбраны мультифрактальные показатели Н_х, Н_у, H_xy, С_х, С_у, C_xy. Применение этих признаков позволило значительно сократить размерность вектора признаков исходного описания изображения. Идентификация помех на изображении проводится путем вычисления мультифрактальных показателей с использованием формул (6), (8). По значениям  мультифрактальных показателей в автоматизированном режиме идентифицируется вид помехи на изображении.

  Предложений метод формирования пространства признаков для идентификации помех на изображении исследовался на примере изображения, пораженном одним из трех видов помех: аддитивной гауссовой, импульсной или мультипликативной. Статистическая модель помеховой ситуации (1)  принимает вид:

¾    в случае аддитивной гауссовой помехи

¾    в случае импульсной помехи

¾    в случае мультипликативной помехи

Экспериментальные исследования предложенного подхода к автоматизированной идентификации шума проведены на изображении размером 256х256 пикселей, в центре которого – белый квадрат 64х64 на черном  фоне. На это изображение накладывались следующие виды помех:

¾    аддитивный гауссовский шум с отношением сигнал/шум по мощности q Î {100; 50; 20; 10; 5; 2; 1}  (класс 1);

¾    импульсный униполярный шум с количеством сбойных пикселей 20%, 15%, 10%, 5%, 1%, 0.5%, 0.1%, причем незашумленное изображение предварительно переводилось на интервал интенсивностей [0,4; 0,5] (класс 2);

¾    мультипликативный горизонтальный, вертикальный, диагональный шум, для которого где частота дискретизации ∆=1/256, ωÎ{0,05 период/м; 0,125 период/м; 0,25 период/м; 0,5 период/м; 1 период/м; 1,5 период/м; 2 период/м; 2,5 период/м; 5 период/м} (класс 3);

¾    мультипликативный горизонтальный, вертикальный, диагональный шум, для которого , где частота дискретизации ∆=1/256, ω=0,5, А определяется т. о., чтобы отношение сигнал/шум q Î {100; 50; 20; 10; 5; 2; 1}  (класс 4).

Отношение сигнал/шум для изображений класса 1 вычислялось по формуле

где  h — величина контраста объекта,  — стандартное отклонение шума; а для изображений класса 4 — по формуле  где А — амплитуда мультипликативной помехи.

            Необходимо было идентифицировать один их трех видов помех по значениям мультифрактальных показателей изображений каждого из перечисленных четырех классов изображений.

            На рис. 3 — 5 представлены значения компонентов вектора признаков Н_х, Н_у, H_xy, С_х, С_у, C_xy, которые используются при идентификации помех для изображений классов 1 — 4.

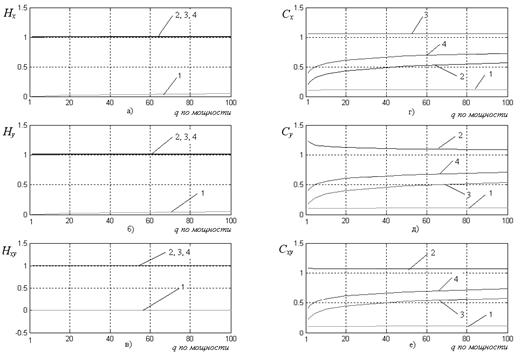
Рис. 3 Зависимость значений Н_х (а), Н_у (б), H_xy (в), С_х (г), С_у (д), C_xy (е) от q для изображений классов 1 — 4:

1 — гауссовский шум;

2 — мультипликативный горизонтальный шум;

3 — мультипликативный вертикальный шум;

4 — мультипликативный диагональный шум.

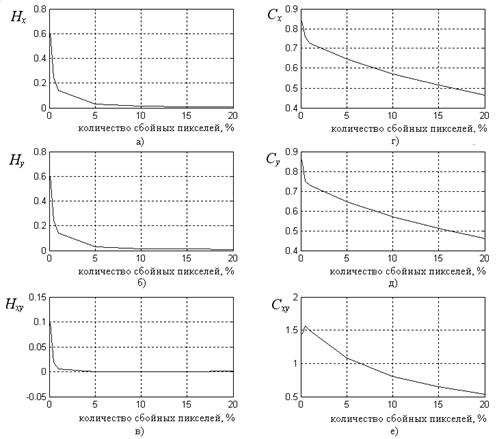
Рис. 4 Зависимость значений Н_х (а), Н_у (б), H_xy (в), С_х (г), С_у (д), C_xy (е) от количества сбойных пикселей для изображений класса 2.

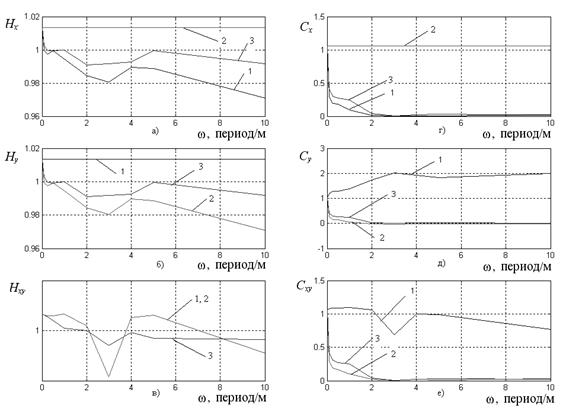
Рис. 5 Зависимость значений Н_х (а), Н_у (б), H_xy (в), С_х (г), С_у (д), C_xy (е) от частоты w для изображений класса 3:

1 — мультипликативный горизонтальный шум;

2 — мультипликативный вертикальный шум;

3 — мультипликативный диагональный шум.

            Анализируя полученные результаты, следует заметить, что мультифрактальные показатели в качестве признаков в задаче идентификации помех изображений обладают разделительными свойствами. Мультипликативная и гауссовская помехи идентифицируются как по признакам Н_х, Н_у, H_xy, так и по признакам С_х, С_у, C_xy. Импульсная и гауссовская помехи различаются значениями С_х, С_у, C_xy, мультипликативная и импульсная помехи характеризуются разными значениями Н_х, Н_у, H_xy. Значения признаков изображений, представляющих мультифрактальные показатели, позволяют не только идентифицировать вид помехи, но и определить параметры шума. Так, отношение сигнал/шум для аддитивной помехи можно получить с использованием значений Н_х, Н_у, которые монотонно возрастают с ростом отношения сигнал/шум. Уровень импульсного шума легко определить по значениям С_х, С_у, C_xy, монотонно убывающим с ростом количества сбойных пикселей. Отношение сигнал/шум для мультипликативной помехи определяется с использованием значений С_х, С_у, C_xy, которые монотонно возрастают с ростом отношения сигнал/шум. Вычисленные значения признаков находятся в соответствии с теоретическими значениями мультифрактальных показателей: для гауссовского шума значения признаков близки к нулю, для импульсного шума Н_х, Н_у, H_xy близки к нулю, для мультипликативного шума Н_х, Н_у, H_xy приблизительно равны единице.

На рис. 6 представлены изображения классов 1 — 4 в двумерных пространствах признаков.

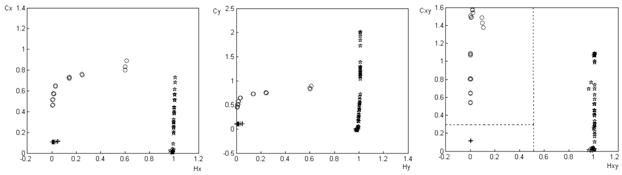
а)                                                    б)                                                 в)

Рис. 6 Изображения классов 1 — 4 в двумерном пространстве признаков {Н_х, С_х} (a), {Н_у,  С_у} (б), {H_xy, C_xy} (в): «+» — класс 1; «о» — класс 2; «¶»— классы 3, 4.

            Выделение границ кластеров на этих рисунках свидетельствует о том, что классы изображений, пораженных гауссовской, импульсной и мультипликативной помехой разнесены в пространстве признаков и формируют ленточные кластеры. Приведем определение ленточного кластера.

Определение [8]. Кластер S_l называется ленточным кластером или кластером типа ленты, если существует t>0 такое, что для любого a_iÎ S_l найдется такой объект a_jÎ S_l, что , а для любого a_kÎA\S_l справедливо , где А — общая совокупность объектов классификации,  — расстояние между объектами класса.

            Предложенный мультифрактальный метод идентификации помех на изображениях позволил выделить кластеры, для которых внутриклассовые средние расстояния меньше межклассовых средних расстояний данного класса. Для иллюстрации приведена матрица средних расстояний (табл. 1).

Таблица 1

Средние межклассовые и внутриклассовые расстояния

            Согласно определению ленточного кластера среднее внутриклассовое расстояние  вычислялось как среднее расстояние между объектами кластера. Использовалась формула

,

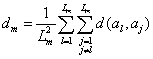где  — расстояние между объектами  кластера , К — размерность вектора признаков  объекта ,  — количество элементов в кластере . Среднее межклассовое расстояние  вычислялось как среднее расстояние между объектами m-го кластера и объектами k-го кластера

,

где .

С использованием матрицы средних расстояний производилось сравнение внутриклассовых расстояний с межклассовыми по t-критерию. Из табл. 1 видно, что средние расстояния достаточно сильно различаются (1 означает существенное (на уровне 5%) отличие среднего межклассового расстояния от среднего внутриклассового). Исследование свойств кластеров в пространстве признаков позволило их разделить с помощью простейших разделяющих поверхностей, определяемых значениями порога. Значения порогов определялись путем анализа гистограмм значений признаков изображений и приведены в табл. 1. Соответствующие значениям порогов разделяющие прямые обозначены на рис. 6, в пунктиром.

            Выводы. Т. о. проведенные исследования показали, что свойства помех на изображении могут быть адекватно представлены с помощью мультифрактальных показателей. Идентификация помех с помощью мультифрактальных показателей производится в автоматизированном режиме. Предложенный мультифрактальный метод автоматизированной идентификации помех позволил получить в признаковом пространстве непересекающиеся кластеры изображений с определенным видом помехи, а именно, изображений, пораженных аддитивным гауссовским или мультипликативным шумом со значениями отношения сигнал/шум 1 — 100 по мощности, мультипликативным шумом с частотой 0,1 — 10 период/м при частоте дискретизации 256 период/м, импульсным шумом с количеством сбойных пикселей 0,1 — 20%. Если помеха на изображении характеризуется отличными от приведенных параметрами, вероятность ошибок распознавания 1-го и 2-го рода, возможно, возрастает. Поэтому направлением дальнейших исследований является развитие предложенного мультифрактального метода идентификации шумов на случай изображений, пораженных одновременно несколькими видами помех.

1.      Гонсалес Р., Вудс Р. Цифровая обработка изображений. — М.: Техносфера, 2005. — 1072 с.

2.      Крылов В.Н., Максимов М.В. Вторичные преобразователи сигналов изображений. — Одесса: Астропринт, 1997. — 176 с.

3.      Гонсалес Р., Ту Дж. Принципы распознавания образов. — М.: Мир, 1978. — 411 с.

4.      El-Maleh K., Samouelian A., Kabal P. Frame-level noise classification in mobile environments // Proceedings of ICASSP. — 1999. — P. 1011 — 1015.

5.      Couvreur A., Bresler K. Dictionary-based decomposition of linear mixtures of Gaussian processes // Proceedings of ICASSP. — 1996. — P. 743 — 747.

6.      Davis A., Marshak A., Wiscombe W., Cahalan R. Multifractal characterizations of nonstationary and intermittency in geophysical fields: Observed, retrieved or simulated // Jornal of Geophysical Research. — 1994. — V. 99, № D4. — P. 8055 — 8072.

7.      Davis A., Marshak A., Gerber H., Warren W. Multifractal characterizations of nonstationary and intermittency in geophysical fields: Observed, retrieved or simulated // Jornal of Geophysical Research. — 1994. — V. 99, № D4. — P. 8055 — 8072.

8.      Мандель И.Д. Кластерный анализ. — М.: Финансы и статистика, 1988. — 176 с.